Elektryczność i magnetyzm
wersja .pdf
Pole elektryczne, kondensatory, przewodniki i dielektryki.
Nieskończenie długą prostą nić znajdującą się w próżni naładowano ze stałą gęstością liniową ładunku
l = 2 x 10-6 C/m.
(a) Wyznacz moduł natężenia pola E i potencjał V jako funkcję odległości r od nici.
(b) Oblicz E i V dla r = 10m.
Ładunki o przeciwnych znakach są rozłożone ze stałymi gęstościami powierzchniowymi
+s i -s odpowiednio na dwóch metalowych płaszczyznach nieskończonych, równoległych względem siebie i odległych o d.
(a) Oblicz i wykreśl zależność potencjału i natężenia pola elektrycznego w funkcji odległości między płytami.
(b) Jak zmieni się rozkład pola, gdy jedną z płyt połączymy z ziemią?
Oblicz pojemność odosobnionej kulki metalowej o promieniu R.
Oblicz, korzystając z definicji pojemności elektrycznej, pojemność kondensatora:
(a) płaskiego,
(b) kulistego,
(c) walcowego.
Pojemność kondensatora:
(a) Płaskiego:
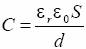
dla
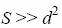
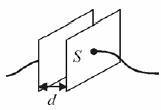
(b) Kulistego:
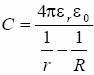
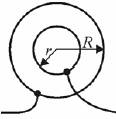
(c) Walcowego:
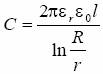
dla
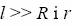
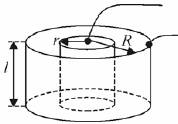
Płaski kondensator naładowano do napięcia U 0 i odłączono od źródła. Jak zmieni się:
(a) napięcie na kondensatorze,
(b) natężenie pole elektrycznego,
(c) ładunek na okładkach, jeżeli okładki zsuniemy na n razy mniejszą odległość?
Do dwóch szeregowo połączonych kondensatorów o pojemnościach C1 = 100pF i C2 = 200pF przyłożono stałe napięcie
U = 300V.
Oblicz napięcia U1 i U2 na kondensatorach i ładunki q1 i q2 na ich okładkach.
Jaka jest pojemność C tego układu?
Płaski kondensator powietrzny, o odległości między okładkami d, naładowano ładunkiem Q.
(a) Jak zmieni się natężenie pola elektrycznego po wprowadzeniu między okładki, równolegle do nich, metalowej płytki o grubości l? Powierzchnie okładek i płytki wynoszą S.
(b) Oblicz pojemność C układu z płytką.
(c) Jak zmieni się napięcie między okładkami w wyniku wprowadzenia płytki?
Kulka rtęci, naładowana do potencjału V, podzieliła się na dwie kulki, z których jedna ma n razy większą objętość od drugiej.
Do jakich potencjałów będą naładowane te kulki?
Każdy z trzech kondensatorów o pojemnościach C1, C2, C3 naładowano do napięcia U i następnie, po odłączeniu źródła napięcia, wszystkie połączono szeregowo (rys. a)
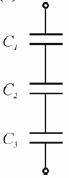
Oblicz ładunki Q 1, Q2, Q3 na okładkach kondensatorów tak otrzymanego układu kondensatorów po zwarciu ich przewodnikiem (rys. b).
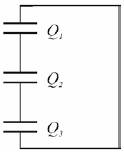
Trzy kondensatory o pojemnościach C1, C2, i C3 połączono jak na rysunku i naładowano ładunkiem Q. Oblicz ładunki na okładkach każdego z kondensatorów.
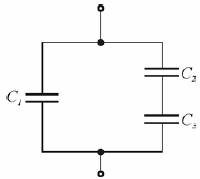
Trzy kondensatory o pojemnościach C1, C2, i C3 połączono jak na rysunku i naładowano ładunkiem Q. Oblicz ładunki na okładkach każdego z kondensatorów.
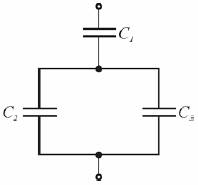
Ile razy trwały moment dipolowy cząsteczki tlenku węgla CO, który wynosi
p0 = 0,37 x 10-30 C/m,
jest większy od momentu dipolowego indukowanego w tej cząsteczce przez zewnętrze pole elektryczne o natężeniu
E = 104 V/cm?
Średnia polaryzowalność elektronowa cząsteczki CO wynosi a = 2,2 F/m2.
W odległości r = 15 x 10-10 m od atomu argonu znajduje się elektron.
Oszacuj moment dipolowy indukowany w atomie argonu przez pole elektryczne elektronu. Polaryzowalność elektronowa atomu argonu wynosi a = 1,8 x 10-40 F/m2 .
Momenty dipolowe molekuł równają się sumie wektorowej odpowiednich momentów dipolowych wiązań. Oblicz moment dipolowy wiązania OH w molekule wody, jeżeli moment dipolowy molekuły wody równa się 6,2 x 10-30 Cm, a kąt między wiązaniami OH wynosi 104o.
Stała elektryczna diamentu wynosi e0 = 1,46 10-10 C/(Nm2 ). Znajdź względną przenikalność er i podatność dielektryczną P diamentu.
Ile wynosi polaryzowalność jednostki objętości i jednego mola diamentu? Gęstość diamentu r = 3,51 g/cm2, masa molowa m = 12 g/mol. Skorzystaj ze wzorów na wektor polaryzacji:
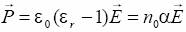
gdzie n0 oznacza koncentrację dipoli.
Jak zmieni się:
(a) pojemność elektryczna,
(b) ładunek na okładkach,
(c) napięcie,
(d) natężenie pola elektrycznego,
jeżeli między elektrody kondensatora płaskiego o pojemności C0 wsuniemy dielektryk o przenikalności er i grubości d równej odległości między okładkami kondensatora?
Rozpatrzyć dwa przypadki:
(I) Kondensator po naładowaniu do napięcia U0 odłączono od źródła.
(II) Kondensator jest cały czas podłączony do źródła o napięciu U0.
Kondensator płaski, którego okładki są oddalone o l = 1cm wypełniony jest olejem (e r= 5).
Jakie napięcie należy przyłożyć do kondensatora, aby gęstość ładunków polaryzacyjnych na oleju wynosiła s = 6,2 x10 -10 C/cm2
Płaski kondensator próżniowy naładowano tak, że natężenie pola wynosi w nim E0 = 100 MV/m. Następnie wypełniono go dielektrykiem, którego drobiny są sztywnymi dipolami o momencie pe = 0,5 x 10 -29 C / m. Koncentracja dipoli n = 10 26 m-3 .
Oblicz średnią wartość natężenia pola elektrycznego wewnątrz dielektryka, pomijając wpływ ruchów cieplnych drobin.
Oblicz gęstość ładunków polaryzacyjnych na powierzchni płytki mikowej (sr = 7) o grubości
l = 0,2 mm, wypełniającej całkowicie płaski kondensator naładowany do napięcia U0 = 400 V. Jak i o ile zmieni się napięcie na kondensatorze po wyjęciu płytki?
Płaski kondensator powietrzny, o pionowo ustawionych okładkach odległych o d, naładowano i zanurzono częściowo w cieczy o względnej przenikalności dielektrycznej er.
Oblicz stosunek ładunków elektrycznych i natężeń pól elektrycznych w obu częściach kondensatora, jeżeli wysokość okładek wynosi H, a wysokość zanurzonej części jest h.
Płaski kondensator o powierzchni elektrod S = 100 cm2 oddalonych od siebie o d = 1 cm naładowano do napięcia U0 = 100 V i odłączono od źródła. Następnie obszar między okładkami kondensatora ściśle wypełniono dwiema płytkami dielektrycznymi o grubościach
d1 = 2 mm i d2= 8 mm, oraz stałych dielektrycznych er1 = 2 i e r2 = 4.
Oblicz:
(a) Ładunek swobodny na okładkach kondensatora.
(b) Wartości wektorów natężenia pola elektrycznego 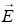 , indukcji elektrostatycznej , indukcji elektrostatycznej 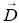 i polaryzacji elektrycznej i polaryzacji elektrycznej 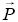 w obu dielektrykach. w obu dielektrykach.
(c) Napięcie na kondensatorze po włożeniu płytki.
(d) Pojemność kondensatora z obu dielektrykami. |