Zadania

2007-03-20 Ostatnia modyfikacja.

Zadanie

Zadanie. Model atomu według Bohra.

Model planetarny atomu według Bohra

Załóż, że model planetarny opisuje ruch elektronu w atomie wodoru. Jeśli promień orbity elektronu wynosi oblicz:

a. częstość kołową elektronu,

b. prędkość liniową elektronu,

c. energię kinetyczną elektronu w eV. Jaka jest minimalna energia potrzebna do zjonizowania atomu?

Rozwiązanie

Oczywiście trzeba pamiętać, że model Bohra jest błędny i nie oparty na żadnych konkretnych przesłankach fizycznych. W zadaniu zakłada się jednak, że atom wodoru jest zbudowany tak jak to opisał Bohr.

Wtedy rozważamy ruch elektronu wokół masywnego jądra*

*Przyjmujemy, i nie jest to wielkim błędem, że środek masy układu jądro elektron znajduje się jądrze. Elektron ma masę. Natomiast proton (stanowiący jądro atomu wodoru) . Jak widać jest to różnica czterech rzędów wielkości.

Pomiędzy elektronem a protonem występuje kulombowskie oddziaływanie przyciągające

Jest to jednocześnie siła dośrodkowa w ruchu po okręgu. Jak pamiętamy z lekcji fizyki siła dośrodkowa wyraża się wzorem

gdzie v prędkość liniowa ciała poruszającego się po okręgu; r promień okręgu; m masa ciała;

W tym zadaniu siła dośrodkowa wygląda następująco:

i jest równa sile oddziaływania elektrostatycznego, więc:

i dostajemy prędkość liniową

Częstość kołową uzyskamy łatwo, gdy zauważymy, że:

więc

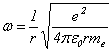
Obliczenie energii kinetycznej też nie stanowi problemu.

Aby obliczyć energię jonizacji trzeba znać całkowitą energię elektronu, czyli nie tylko energię kinetyczną, ale i potencjalną. Suma tych energii daje energię całkowitą i dla stanów związanych* jest zawsze ujemna.

*Elektron i jądro w atomie tworzą stan związany, podobnie w stanie związanym są Ziemia i Księżyc czy Ziemia i stacja orbitalna. Gdy ludzie wysyłają sondy kosmiczne poza układ słoneczny to nadają im taką energię, aby nie tworzyły stanów związanych z innymi planetami.

Energia potencjalna układu proton-elektron wyraża się wzorem