 Promieniowanie termiczne. Katastrofa w nadfiolecie.
Promieniowanie termiczne. Katastrofa w nadfiolecie.
Promieniowanie
wysyłane przez ciało ogrzane do pewnej temperatury
nazywane jest promieniowaniem termicznym (cieplnym
lub temperaturowym). Wszystkie ciała emitują takie
promieniowanie do swojego otoczenia, a także z tego
otoczenia je absorbują. Jeśli na początku ciało ma
wyższą temperaturę niż jego otoczenie, ciało to będzie
się oziębiać, ponieważ szybkość wypromieniowywania
przez nie energii będzie przewyższała szybkość jej
absorpcji. Gdy zostanie osiągnięta równowaga termodynamiczna,
wtedy szybkość emisji będzie równa szybkości absorpcji.
Materia
w stanie skondensowanym (ciała stałe, ciecze) emituje
promieniowanie o widmie ciągłym. Szczegóły tego widma
są prawie niezależne od rodzaju substancji, z której
zbudowane jest ciało, natomiast zależą one silnie
od temperatury ciała. W zwykłych temperaturach większość
ciał jest dla nas widoczna nie dlatego, że ciała te
wysyłają światło, ale dlatego, że je odbijają lub
rozpraszają. Jeśli na takie ciało nie pada światło,
to jest ono niewidoczne. Jednak gdy ciała mają wysoką
temperaturę, wtedy świecą własnym światłem. Możemy
je widzieć, jak się żarzą w ciemnym pokoju. Ale nawet
w temperaturach tak wysokich jak kilka tysięcy kelwinów
ogromna część, bo ponad 90% emitowanego promieniowania
cieplnego jest dla nas niewidzialna, należy ona bowiem
do obszaru widma promieniowania elektromagnetycznego
zwanego podczerwienią. Dlatego też ciała, które świecą
własnym światłem muszą być bardzo gorące.
Szczegółowa
postać widma promieniowania termicznego wysyłanego
przez gorące ciało zależy w pewnym stopniu od składu
tego ciała. Z doświadczeń wynika, że istnieje klasa
rozgrzanych ciał, które emitują promieniowanie o widmie
mającym charakter uniwersalny. Są one nazywane
ciałami doskonale czarnymi, tzn. ciałami, których
powierzchnie absorbują całe promieniowanie nań padające.
Nazwa taka wydaje się bardzo odpowiednia, ponieważ
ciała te nie odbijają światła i wobec tego można je
uznać za czarne (nie należy mylić z ciałami o kolorze
czarnym).
Jak w
praktyce realizujemy ciała doskonale czarne? Robi
się pudło z bardzo małym otworkiem i wnętrze tego
pudła pokrywa się sadzą (sadza ma bardzo dobre własności
pochłaniania promieniowania). Wówczas promieniowanie
wpadające w ten otworek odbija się wielokrotnie od
powierzchni wewnętrznej pudła, a ponieważ ma ona bardzo
mały współczynnik odbicia, więc po kilkunastu odbiciach
promieniowanie zostaje zaabsorbowane przez pudło.
Dla metalowego
pudła wyścielonego sadzą, obserwuje się otwór i mierzy
rozkład widmowy promieniowania, który jest jednakowy
dla wszystkich ciał doskonale czarnych. Nie zależy
ono ani od składu chemicznego, ani od wymiarów geometrycznych.
Fakt ten można wyjaśnić opierając się na klasycznych
rozważaniach równowagi termodynamicznej. Jednakże
na gruncie samych tylko rozważań termodynamicznych
nie można wyznaczyć dokładnego kształtu krzywej opisującej
widmo promieniowania.
Rozkład
widmowy promieniowania ciała doskonale czarnego charakteryzuje
funkcja 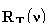 zwana zdolnością emisyjną ciała, zdefiniowana w ten sposób,
że wielkość zwana zdolnością emisyjną ciała, zdefiniowana w ten sposób,
że wielkość 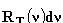 jest równa energii promieniowania o częstotliwości leżącej
w przedziale od jest równa energii promieniowania o częstotliwości leżącej
w przedziale od 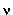 do do 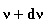 , wysyłanego w ciągu jednostki czasu przez jednostkę powierzchni
ciała mającego temperaturę bezwzględną T. , wysyłanego w ciągu jednostki czasu przez jednostkę powierzchni
ciała mającego temperaturę bezwzględną T.
Otrzymaną
doświadczalnie zależność 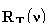 od od 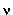 oraz od T przedstawia rysunek: oraz od T przedstawia rysunek:
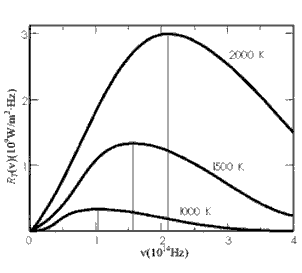
Całka
ze zdolności emisyjnej 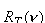 po wszystkich częstotliwościach po wszystkich częstotliwościach 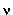 jest równa całkowitej energii wyemitowanej w ciągu jednostki
czasu z jednostki powierzchni ciała doskonale czarnego
o temperaturze T. Jest ona zwana całkowitą
zdolnością emisyjną RT: jest równa całkowitej energii wyemitowanej w ciągu jednostki
czasu z jednostki powierzchni ciała doskonale czarnego
o temperaturze T. Jest ona zwana całkowitą
zdolnością emisyjną RT:
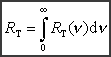
Ze wzrostem
temperatury wielkość RT gwałtownie
wzrasta. Stanowi to treść prawa Stefana:
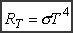 , ,
gdzie
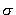 ( (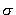 = 5,67,10-8 W/m2K4) jest
stałą Stefana - Boltzmanna. = 5,67,10-8 W/m2K4) jest
stałą Stefana - Boltzmanna.
Ze wzrostem
temperatury T widmo promieniowania ulega przesunięciu
w stronę krótszych długości fali. Fakt ten wyraża
prawo przesunięć Wiena
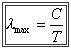
gdzie
C = 2898 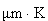 , , 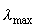 jest długością fali, dla której jest długością fali, dla której 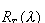 ma w danej temperaturze T wartość maksymalną. ma w danej temperaturze T wartość maksymalną.
Wszystkie
podane wyżej stwierdzenia pozostają w zgodzie z prostymi
faktami doświadczalnymi omawianymi uprzednio, a mianowicie
gdy temperatura ciała wzrasta, wtedy ilość emitowanego
promieniowania gwałtownie wzrasta, a długość fali
promieniowania odpowiadająca maksymalnej zdolności
emisyjnej - maleje (kolor rozgrzewanych przedmiotów
zmienia się od czerwonego do niebiesko-białego).
Klasyczna
teoria promieniowania ciała doskonale czarnego.
Rozważmy
pudło (ciało doskonale czarne) emitujące promieniowanie.
Fale elektromagnetyczne są falami poprzecznymi. Wektor
pola elektrycznego E jest prostopadły do kierunku
rozchodzenia się fali, a ponieważ kierunek rozchodzenia
się rozważanej składowej jest prostopadły do odbijającej
ścianki, więc wektor E jest równoległy do tej
ścianki. Na powierzchni metalowej ścianki nie może
jednak występować równoległe do niej pole elektryczne,
bowiem ładunki elektryczne zawsze mogą przemieścić
się w taki sposób, że zneutralizują to pole. Dlatego
też, w przypadku rozważanej składowej promieniowania,
wartość E na ściance x = 0
musi być zawsze równa zeru. Fala stojąca w płaszczyźnie
prostopadłej do x musi zatem mieć węzeł na
tej ściance. Fala ta musi także mieć węzeł na powierzchni
x = a. Podobne rozważania
stosują się także do pozostałych dwóch kierunków.
Warunki te nakładają ograniczenia na możliwe długości
fal, a więc i na częstotliwości promieniowania elektromagnetycznego
zawartego we wnęce.
Spróbujmy
podejść do zagadnienia w taki sposób, na jaki pozwalał
poziom wiedzy pod koniec XIX w. Dobrze była wówczas
rozwinięta termodynamika, znano równania stanu gazu
oraz sposób opisywania układów termodynamicznych.
Zastosujmy tę wiedzę dla opisania gazu, którym jest
gaz fotonów.
Należy
tu jeszcze przypomnieć zasadę ekwipartycji energii,
która mówi, że na każdy składnik energii zależny od
kwadratu pędu i położenia przypada kT//2 energii(k
- stała Boltzmanna). Każda fala stojąca niesie ze
sobą średnią energię: 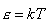 . Żeby policzyć całą energię emisyjną musimy pomnożyć
energię jednej fali przez liczbę fal, które mogą w
takim pudle powstać. Innymi słowy musimy uwzględnić
gęstość promieniowania. . Żeby policzyć całą energię emisyjną musimy pomnożyć
energię jednej fali przez liczbę fal, które mogą w
takim pudle powstać. Innymi słowy musimy uwzględnić
gęstość promieniowania.
Rozważmy
najpierw jedynie samą składową x, tzn. przeanalizujemy
uproszczony, nie mający odpowiednika w rzeczywistości
przypadek jednowymiarowej wnęki o długości a.
Ponieważ
we wnęce powstają fale stojące, więc musi być spełniony
warunek
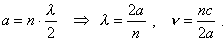
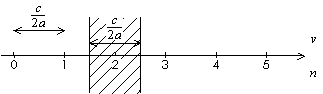
Na
ten obszar przypada 1 stan, ale fale elektromagnetyczne
mogą mieć dwa kierunki polaryzacji, czyli w tym obszarze
realizowane są dwie fale. Zatem gęstość stanów
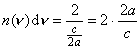
Rozpatrzmy
rezonator trójwymiarowy. Aby policzyć gęstość stanów
dla danej częstotliwości, należy skonstruować w przestrzeni
wektora falowego powierzchnie stałej energii, którą
jest sfera o promieniu 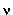 . Jeden stan przypada na odległość c/2a w przestrzeni
jednowymiarowej, więc w przestrzeni trójwymiarowej
będzie to (c/2a)3. Wraz z
objętością sfery określonej dla dodatnich . Jeden stan przypada na odległość c/2a w przestrzeni
jednowymiarowej, więc w przestrzeni trójwymiarowej
będzie to (c/2a)3. Wraz z
objętością sfery określonej dla dodatnich 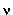 , daje to: , daje to:
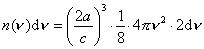 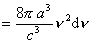
tyle
drgań może się zrealizować w pudle rezonansowym o wymiarze
a.
Zdolność
emisyjna na jednostkę objętości  T T
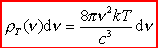
Jest
to wzór Rayleigha - Jeansa dla promieniowania ciała
doskonale czarnego.
Wzór ten poprawnie opisuje wartości eksperymentalne
tylko dla małych  . Zasadniczo jednak nie zgadza się z eksperymentem. Fakt
ten nazwano "katastrofą w nadfiolecie", gdyż ciała
wypromieniowałyby całą energię w zakresie nadfioletu. . Zasadniczo jednak nie zgadza się z eksperymentem. Fakt
ten nazwano "katastrofą w nadfiolecie", gdyż ciała
wypromieniowałyby całą energię w zakresie nadfioletu.
Teoria Plancka promieniowania we wnęce.
Planck stwierdził, że w przypadku promieniowania
ciała doskonale czarnego średnia energia fal stojących
jest funkcją częstotliwości. Stwierdzenie to było
w jawnej sprzeczności z prawem ekwipartycji energii,
które średniej energii przypisuje wartość niezależną
od częstotliwości.
Na podstawie obliczeń dla oscylatorów Planck oszacował,
że do opisu promieniowania należy brać układ o wartościach
energii odpowiednio skwantowanych, a nie ciągłych.
Odkrył, że dla małej różnicy 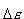 między kolejnymi wartościami energii otrzymuje się między kolejnymi wartościami energii otrzymuje się 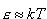 , natomiast dla dużego , natomiast dla dużego 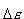 wartość średnia energii wartość średnia energii 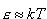 . Ponieważ pierwszy z tych wyników był potrzebny dla małych
częstotliwości, a drugi dla dużych, więc Planck musiał
przyjąć, że . Ponieważ pierwszy z tych wyników był potrzebny dla małych
częstotliwości, a drugi dla dużych, więc Planck musiał
przyjąć, że 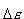 jest rosnącą funkcją jest rosnącą funkcją 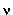 : :
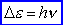
gdzie h = 6,63 10-34 J 10-34 J s jest stałą Plancka. s jest stałą Plancka.
Wyrażenie
na 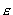 , które uzyskał Planck to: , które uzyskał Planck to:
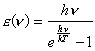
| Ponieważ |
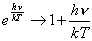 |
(dla |
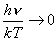 |
),
więc w granicy tej |
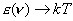 ; ; |
| z
kolei dla |
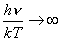 |
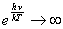 |
i |
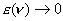 |
czyli
wyniki pokrywają się z obserwacjami. |
Wyrażenie
na gęstość energii promieniowania ciała doskonale
czarnego, otrzymane przez Plancka i zwane wzorem
Plancka na rozkład widmowy promieniowania ciała doskonale
czarnego, ma postać:
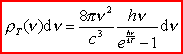
Wielki
wkład Plancka do teorii zjawisk fizycznych można przedstawić
w postaci następującego postulatu:
Dowolny
obiekt fizyczny o jednym stopniu swobody, którego
"współrzędna" jest sinusoidalną funkcją czasu (a więc
wykonuje proste drgania harmoniczne), może mieć tylko
taką energię całkowitą, która spełnia związek
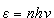 n = 0,1,2,... n = 0,1,2,...
gdzie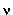 jest częstotliwością drgań, a h jest stałą uniwersalną. jest częstotliwością drgań, a h jest stałą uniwersalną.
Termin
"współrzędna" użyty jest tu w ogólnym sensie i oznacza
każdą wielkość opisującą chwilowy stan danego obiektu
fizycznego. Przykładami takiej współrzędnej są: długość
sprężyny, amplituda fali; wielkości te są sinusoidalnymi
funkcjami czasu.
Kolejnym krokiem było wyprowadzenie praw: Wiena i
Stefana.
Prawo
przesunięć Wiena:
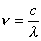 |
-
zależność nieliniowa, więc |
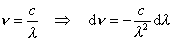 |
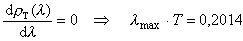 |
hc/K |
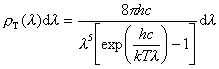
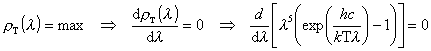
co
prowadzi do równania
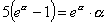 |
gdzie |
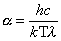 |
Rozwiązaniem powyższego równania jest
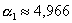
co daje
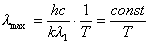
Prawo Stefana:
Nagrody
Nobla dla Wiena (1911 r.) i Plancka (1918 r.)
Na podstawie
widma promieniowania cieplnego można określić temperaturę
ciała. Służą do tego przyrządy zwane pirometrami.
Przykładem promieniowania temperaturowego jest tzw.
promieniowanie reliktowe odkryte w 1961 r. przez A.
Penziasa (nagroda Nobla w 1978 r.). Jest to promieniowanie
o temperaturze 2,735 K będące pozostałością
po wielkim wybuchu sprzed ok.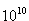 lat. lat.
|