 Postulaty
fizyczne mechaniki kwantowej.
Postulaty
fizyczne mechaniki kwantowej.
Równanie Kleina - Gordona.
Postulaty
fizyczne
Każdemu
eksperymentowi towarzyszy nieuniknione zakłócenie,
np. żeby zlokalizo-wać elektron, musimy go oświetlić,
a foton oddziałuje z elektronem i zaburza jego pęd.
Takie zaburzenie na poziomie atomowym jest już istotne.
-
Zasada
odpowiedniości.
Wszystkie relacje znane
z mechaniki klasycznej, które nie zawierają pochodnej,
zachodzą również w mechanice kwantowej, po zastąpieniu
wielkości fizycznych odpowiednimi operatorami.
Dla układów makroskopowych musi nastąpić automatyczne
przejście z mechaniki kwantowej w mechanikę klasyczną;
nowa i stara teoria muszą się zgadzać w zakresie,
gdzie różnice pomiędzy ich założeniami nie odgrywają
istotnej roli.
-
Zasada
komplementarności.
Pewne elementy opisów układów
mikroskopowych wykluczają się wzajemnie.
Z empirycznego punktu widzenia żaden przyrząd
nie pozwala zmierzyć dokładniej niż to wynika
z zasady nieoznaczoności, tzn. jest to bariera
teoretyczna, a nie względy praktyczne.
- Zasada
superpozycji.
Zakładamy, że równanie
falowe, które opisuje pojedynczą cząstkę musi
być równaniem liniowym.
Jeżeli mamy jakieś równanie opisujące jeden obiekt
i dodamy drugi, to równanie to musi opisywać dwa
obiekty. Jest to bardzo ograniczające założenie
i są takie dziedziny fizyki, jak optyka nieliniowa,
gdzie zasada ta nie gra żadnej roli.
Równanie
Kleina - Gordona
Równanie to opisuje propagację fal w pustej przestrzeni.
Niezmiennik:
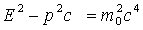
Równanie fali płaskiej de Broglie'a:
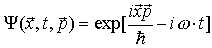
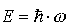
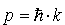
Różniczkujemy funkcję falową dwukrotnie po czasie:
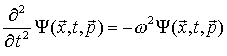
Różniczkujemy funkcję falową dwukrotnie względem x:
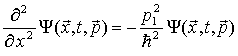
Wstawiając do niezmiennika, otrzymujemy:
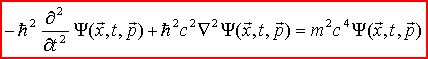
Powyższe
równanie znane jest jako równanie Kleina - Gordona.
Jeżeli
rozpatrujemy ogólniejszą (ciągłą) superpozycję fal
po całej przestrzeni R3, wówczas
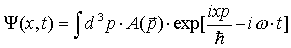 , ,
gdzie 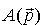 jest funkcją wektora jest funkcją wektora 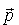 przyjmującą wartości zespolone. Równanie to jest najogólniejszą
postacią równania fali de Broglie'a. przyjmującą wartości zespolone. Równanie to jest najogólniejszą
postacią równania fali de Broglie'a.
Z równania
Kleina - Gordona po podzieleniu przez 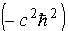 otrzymujemy: otrzymujemy:
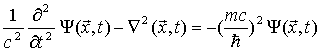
Jest
to liniowe równanie różniczkowe na funkcję falową
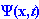 . .
|