 Zjawisko Comptona. Zjawisko Comptona.
W 1923
roku A.H. Compton odkrył zjawisko rozpraszania promieni
rentgenowskich na cząstkach naładowanych (nagroda
Nobla 1927 r).
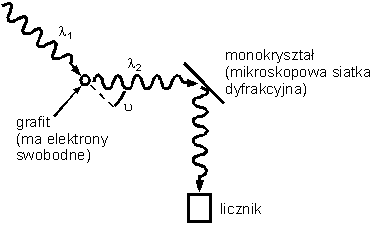
W swoich
doświadczeniach Compton stosował wiązkę promieniowania
rentgenowskiego o ściśle określonej długości fali 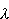 1 i kierował ją na grafitową tarczę. Dla
różnych kątów rozproszenia mierzył on natężenie
rozproszonego promieniowania rentgenowskiego w funkcji
długości fali. 1 i kierował ją na grafitową tarczę. Dla
różnych kątów rozproszenia mierzył on natężenie
rozproszonego promieniowania rentgenowskiego w funkcji
długości fali.
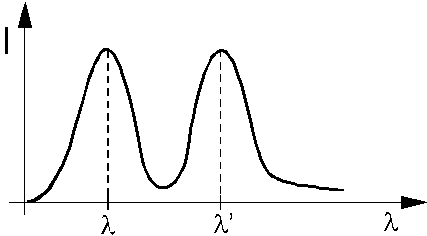
Rys. Natężenie wiązki rozproszonej pod kątem 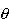 w zależności od długości fali ( w zależności od długości fali (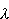 = =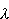 1, 1, 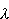 '= '=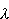 2). 2).
Łatwo
zauważyć, że chociaż wiązka padająca zawiera w zasadzie
jedną długość fali 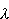 1, rozkład natężenia rozproszonego
promieniowania rentgenowskiego ma maksima dla dwu
długości fali. Jedna długość fali równa jest długości
fali padającej, druga 1, rozkład natężenia rozproszonego
promieniowania rentgenowskiego ma maksima dla dwu
długości fali. Jedna długość fali równa jest długości
fali padającej, druga 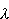 2 jest od niej większa o wielkość 2 jest od niej większa o wielkość 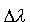 . To tak zwane przesunięcie komptonowskie . To tak zwane przesunięcie komptonowskie 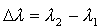 zmienia się wraz z kątem, pod którym
obserwujemy rozproszone promieniowanie rentgenowskie. zmienia się wraz z kątem, pod którym
obserwujemy rozproszone promieniowanie rentgenowskie.
Pojawienia
się promieniowania rozproszonego o długości fali 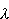 2 nie można wytłumaczyć, jeśli
padające promieniowanie traktuje się jako klasyczną
falę elektromagnetyczną. 2 nie można wytłumaczyć, jeśli
padające promieniowanie traktuje się jako klasyczną
falę elektromagnetyczną.
Compton
postulował, że padająca wiązka promieniowania rentgenowskiego
nie jest falą o częstotliwości 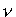 , lecz strumieniem fotonów, z których każdy
ma energię , lecz strumieniem fotonów, z których każdy
ma energię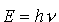 . Fotony te zderzają się ze swobodnymi
elektronami tarczy, podobnie jak zderzają się ze
sobą kule bilardowe. Ponieważ padające fotony podczas
zderzeń przekazują część swojej energii elektronom,
więc rozproszony foton musi mieć energię E2 mniejszą od E1, a zatem i niższą
częstotliwość, co z kolei daje większą długość fali.
Taka interpretacja Comptona jakościowo wyjaśnia
obserwowaną zmianę długości fali wiązki rozproszonej.
Zauważmy, że rozważając oddziaływanie promieniowania
z elektronami tarczy, wiązkę promieniowania traktujemy
jako strumień cząstek, a nie jako falę. Ponadto
w odróżnieniu od zjawiska fotoelektrycznego fotony
w zjawisku Comptona są raczej rozpraszane a nie
absorbowane. Przeanalizujmy teraz ilościowo proces
zderzenia pojedynczego fotonu z elektronem. . Fotony te zderzają się ze swobodnymi
elektronami tarczy, podobnie jak zderzają się ze
sobą kule bilardowe. Ponieważ padające fotony podczas
zderzeń przekazują część swojej energii elektronom,
więc rozproszony foton musi mieć energię E2 mniejszą od E1, a zatem i niższą
częstotliwość, co z kolei daje większą długość fali.
Taka interpretacja Comptona jakościowo wyjaśnia
obserwowaną zmianę długości fali wiązki rozproszonej.
Zauważmy, że rozważając oddziaływanie promieniowania
z elektronami tarczy, wiązkę promieniowania traktujemy
jako strumień cząstek, a nie jako falę. Ponadto
w odróżnieniu od zjawiska fotoelektrycznego fotony
w zjawisku Comptona są raczej rozpraszane a nie
absorbowane. Przeanalizujmy teraz ilościowo proces
zderzenia pojedynczego fotonu z elektronem.
Korzystamy
z niezmiennika relatywistycznego:
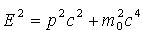
| Dla
fotonu |
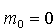 |
,
więc |
 |
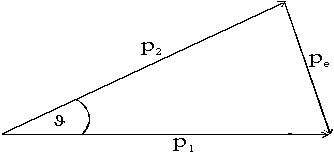
| zasada
zachowania pędu: |
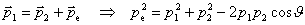 |
| Zasada
zachowania energii: |
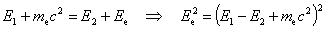 |
Otrzymane 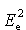 i i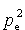 wstawiamy do niezmiennika relatywistycznego: wstawiamy do niezmiennika relatywistycznego: 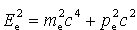
Dokonujemy
przekształceń
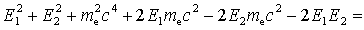
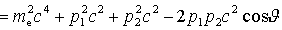
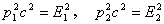
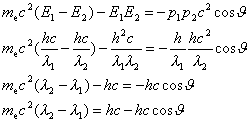
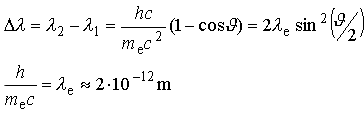 gdzie
gdzie 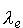 jest to tzw. komptonowska długość fali
elektronu. jest to tzw. komptonowska długość fali
elektronu.
Zjawisko
Thomsona.
Obecność
maksimum odpowiadającego fotonom rozproszonym o
niezmienionej długości fali nadal wymaga wyjaśnienia. Proces rozpraszania fotonów bez zmiany długości fali
nazywany jest rozpraszaniem Thomsona.
Interpretacja
kwantowa.
Cały
czas zakładaliśmy, że elektron, z którym foton się
zderza, jest elektronem swobodnym. Jednak jeśli
elektron jest początkowo związany, powyższe założenie
jest uzasadnione, kiedy tylko energia kinetyczna
uzyskiwana przez elektron podczas zderzenia jest
dużo większa od energii wiązania tego elektronu.
Jeśli natomiast elektron jest silnie związany w
atomie tarczy lub gdy energia padającego fotonu
jest bardzo mała, wtedy istnieje pewne prawdopodobieństwo,
że elektron nie zostanie od atomu oderwany. W takim
przypadku zderzenie może być traktowane jako zderzenie
fotonu z całym atomem. Wtedy masą charakterystyczną
dla procesu jest masa M atomu i we wzorze
na przesunięcie Comptona należy ją podstawić w miejsce
masy elektronu me. Ponieważ M>>me,
przesunięcie komptonowskie dla takich zderzeń, w
których elektrony są silnie związane, jest tak małe,
że doświadczalnie nie daje się wyznaczyć. Tak więc
rozproszony foton ma w zasadzie niezmienioną długość
fali.
Niektóre
fotony są rozpraszane na elektronach, które w następstwie
zderzenia są uwalniane; długość fali tych fotonów
ulega zmianie. Inne fotony są rozpraszane na elektronach,
które mimo zderzenia pozostają związane w atomie;
długość fali tych fotonów nie ulega zmianie.
Interpretacja
klasyczna.
Thomson
rozważał promieniowanie rentgenowskie jako wiązkę
fal elektromagnetycznych. Drgający wektor pola elektrycznego
fali działa na elektrony atomów tarczy. W rezultacie
na elektron działa siła wprawiająca go w drgania,
a więc wywołująca ruch przyspieszony. Elektron poruszający
się ruchem przyspieszonym wypromieniowuje fale elektromagnetyczne
o tej samej częstotliwości co fale padające oraz
będące z nimi w zgodnej fazie. Tak więc elektrony
atomów mogą pochłaniać energię z padającej wiązki
promieniowania rentgenowskiego i rozpraszać ją we
wszystkich kierunkach. Przy tym długość fali promieniowania
rozproszonego jest taka sama jak promieniowania
padającego.
Chociaż
klasyczne wyjaśnienie istnienia rozpraszania Thomsona
jest różne od kwantowego, to oba podejścia wyjaśniają
obserwowane doświadczalnie fakty. Stąd wnioskujemy,
że rozpraszanie Thomsona jest przykładem zjawiska,
przy interpretacji którego wyniki teorii klasycznej
i kwantowej się pokrywają.
Nasuwa
się pytanie, w jakim zakresie widma elektromagnetycznego
dominującym procesem będzie rozpraszanie Thomsona,
a w jakim rozpraszanie Comptona. Dla 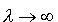 dominuje rozpraszanie Thomsona. Gdy przechodzimy
do zakresu promieniowania rentgenowskiego rozpraszanie
Comptona zaczyna odgrywać coraz większą rolę, szczególnie
dla tarcz rozpraszających złożonych z atomów o małej
liczbie atomowej. W przypadku takich tarcz elektrony
nie są silnie związane w atomach i w konsekwencji
zmiana długości fali w procesie rozpraszania na
elektronie, który w rezultacie zostaje uwalniany,
staje się łatwo mierzalna. W przypadku promieniowania
gamma, dla którego można przyjąć, że dominuje rozpraszanie Thomsona. Gdy przechodzimy
do zakresu promieniowania rentgenowskiego rozpraszanie
Comptona zaczyna odgrywać coraz większą rolę, szczególnie
dla tarcz rozpraszających złożonych z atomów o małej
liczbie atomowej. W przypadku takich tarcz elektrony
nie są silnie związane w atomach i w konsekwencji
zmiana długości fali w procesie rozpraszania na
elektronie, który w rezultacie zostaje uwalniany,
staje się łatwo mierzalna. W przypadku promieniowania
gamma, dla którego można przyjąć, że 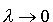 , energia fotonu staje się tak duża, iż
w procesie zderzenia elektron jest zawsze uwalniany
i w rezultacie dominuje rozpraszanie komptonowskie.
Właśnie w zakresie fal krótkich teoria klasyczna
nie jest w stanie wyjaśnić zjawiska rozpraszania
promieniowania. , energia fotonu staje się tak duża, iż
w procesie zderzenia elektron jest zawsze uwalniany
i w rezultacie dominuje rozpraszanie komptonowskie.
Właśnie w zakresie fal krótkich teoria klasyczna
nie jest w stanie wyjaśnić zjawiska rozpraszania
promieniowania. |