Zadanie

Zadanie.

Wyznacz dozwolone wartości energii i funkcje falowe cząstki o masie m znajdującej się w nieskończenie głębokiej, prostokątnej studni potencjału o szerokości L.

Rozwiązanie

Rozwiązanie

Sposobów rozwiązania jest kilka. Przedstawię najprostszy. Aby dotyczył też pozostałych zadań przyjmijmy, że potencjał jest następujący

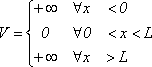
Tam gdzie potencjał jest nieskończenie duży funkcja falowa nie istnieje. W przedziale zerowego potencjału mogą występować funkcje falowe odpowiadające cząstce swobodnej poruszającej się w prawo oraz cząstce swobodnej poruszającej się w lewo. Dodatkowo na brzegach studni funkcja falowa musi znikać. Potencjał nie zależy od czasu, więc zrezygnujemy z pisania członów funkcji falowej zależnych od czasu. Uwzględniając to można napisać:

czyli

wynika z tego, że A + B = 0 więc B = -A.

Można już zapisać jako

Przechodząc do zapisu trygonometrycznego  ma postać

W sposób naturalny dla  ale trzeba też pamiętać o tym, że

gdzie n=1,2,3,4...

Funkcję falową trzeba jeszcze unormować:

po obliczeniu całki

Po uwzględnieniu wartości A oraz k funkcja  przybiera postać

Co po uwzględnieniu czynnika zależnego od czasu daje pełną funkcję falową

Działając hamiltonianem na funkcję falową dostajemy wartości energii dla stanów własnych prostokątnej nieskończonej studni kwantowej.

E jest wartością własną hamiltonianu, czyli energią cząstki. Po podstawieniu funkcji falowej otrzymamy

czyli

Energia cząstki po uwzględnieniu wartości k wyraża się wzorem

gdzie n=1,2,3...

Warto zauważyć, że cząstka w studni potencjału nie może przyjmować dowolnej energii. Poziomy energetyczne są skwantowane.

Odpowiedź

 

Dyskusja

Warto zauważyć, że cząstka w studni potencjału nie może przyjmować dowolnej energii. Poziomy energetyczne są skwantowane.

Podstawa teoretyczna

Artykuły na stronie

Fale de Broglie'a

Postulaty kwantowe

Mechanika falowa Schrödingera

Nieoznaczoność i inne rzeczy

Newton kontra Schrödinger

Kot Schrödingera

Linki

...

Zadania z przedmiotu

Zadania z fizyki kwantowej