Mechanika falowa Schrödingera (operatory, postulaty).

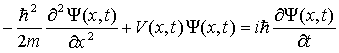
Powyższe równanie, zwane równaniem Schrödingera, spełnia wszystkie cztery założenia o postaci kwantowego równania falowego.

Postulaty równania Schrödingera

Zakładamy, że każda obserwowana własność reprezentowana jest przez operator. Takie własności mierzalne zwane są obserwablami.
Operatory działają na funkcje, które reprezentują stany układu i są nazywane funkcjami stanu (funkcjami falowymi).

1. Jedynymi możliwymi wynikami obserwacji operatora 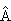są odpowiednie wartości własne operatora (najpierw obserwabli trzeba przyporządkować odpowiedni operator, a później wyliczyć jego wartości własne).

2. Wynikiem obserwacji operatora 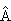wykonanej na układzie w stanie własnym 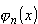jest na pewno wartość własna a_n.

3. Wartość średnia obserwacji 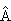powtarzanych na zbiorze układów, z których każdy znajduje się w dowolnym stanie 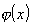wyraża się wzorem

   

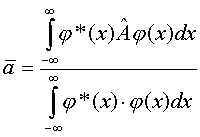
   Diarc wymyślił swoją własną notację :

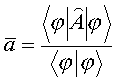
   zapis operatorowy

4. Przedstawienie Schrödingera

   zatem

   

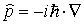
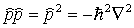
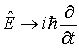
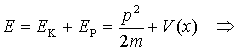
   1D:

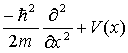
   3D:

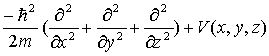
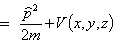
5. W 3D operatorowo :

6. równanie Schrödingera (wynika z dwóch poprzednich).

   Definiuje się następujący operator :

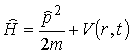
   zwany " hamiltonianem" , wtedy równanie Schrödingera da się nawet zapamiętać!

   

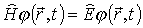
   Relacja między pędem a energią też w końcu jest widoczna.

7. Interpretacja Borna: gęstość prawdopodobieństwa znalezienia cząstki w punkcie x, w chwili t jest równa kwadratowi wartości bezwzględnej funkcji falowej

   

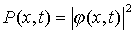
Należy podkreślić, że nie możemy się spodziewać, aby równanie Schrödingera zachowywało swoją ważność w odniesieniu do cząstek poruszających się z relatywistycznymi prędkościami. Zakładaliśmy bowiem, aby było ono zgodne z klasycznym wyrażeniem na energię, które przestaje być słuszne dla dużych prędkości. Równanie to także nie uwzględnia przypadku kreacji i anihilacji par –zakłada stałą liczbę cząstek obdarzonych masą.

Równanie Schrödingera jest zależne od przestrzeni i czasu. Można go uprościć, jeżeli potencjał nie zależy od czasu:







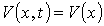
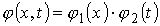
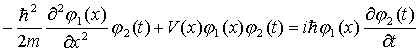
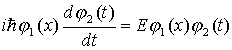
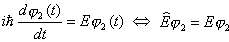
	Rozwiązując równanie własne ...
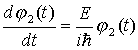
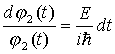
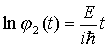
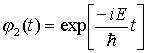
	... znajdujemy funkcję własną operatora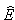

Równanie Schrödingera niezależne od czasu:



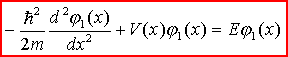
Niezależnie od czasu równanie Schrödingera jest równaniem własnym operatora energii



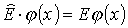
gdzie:



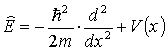
E i 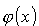są to wartości i funkcje własne powyższego równania własnego.