 Nieoznaczoność i inne rzeczy
Nieoznaczoność i inne rzeczy
W roku 1927 Heisenberg sformułował swą zasadę nieoznaczoności, wieńczącą tę wielką naukową rewolucję, którą zwiemy teorią kwantową. Prawdę mówiąc, rozwój teorii kwantowej trwał aż do lat czterdziestych. a właściwie - w wersji kwantowej teorii pola - ewoluuje ona do dziś i proces ten nie zostanie zakończony, dopóki nie dojdzie do całkowitego jej połączenia z grawitacją. Jednak dla naszych celów zasada nieoznaczoności stanowi odpowiednie zakończenie. Zasada ta, sformułowana przez Heisenberga, jest matematyczną konsekwencją równania Schrödingera. Mogłaby także być postulatem logicznym, czy też założeniem, nowej mechaniki kwantowej. Ponieważ bez zapoznania się z ideą Heisenberga nie zrozumiemy, jak nowy i inny jest świat kwantowy, powinniśmy się tu na chwilę zatrzymać.
Wszyscy fizycy kwantowi utrzymują, że liczą się tylko pomiary - drogie sercu eksperymentatora. Od teorii wymagamy jedynie, by przewidywała rezultaty mierzalnych zdarzeń. Zdanie to brzmi jak truizm, ale zapominanie o tym prowadzi do tak zwanych paradoksów, do których lubią się odwoływać pozbawieni wykształcenia popularyzatorzy. a muszę tu dodać, że to właśnie należąca do teorii kwantowej teoria pomiaru jest jej najbardziej kontrowersyjnym aspektem.
Heisenberg oznajmił, że nasza jednoczesna wiedza o położeniu cząstki i jej ruchu jest ograniczona i że połączona nieokreśloność tych dwóch wielkości musi być większa od... ni mniej, ni więcej, tylko właśnie od stałej Plancka h , którą po raz pierwszy spotkaliśmy we wzorze
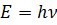
Dokładności pomiaru położenia cząstki i jej ruchu (a ściślej jej pędu) są do siebie odwrotnie proporcjonalne. Im więcej wiemy o jednej wielkości, tym mniej wiemy o drugiej. Równanie Schrödingera podaje nam wartości prawdopodobieństwa dla tych wielkości. Jeśli nawet udałoby się nam obmyślić jakiś eksperyment, w wyniku którego dokładnie wyznaczymy położenie elektronu - powiedzmy, podając jakąś współrzędną z minimalnym błędem - to rozrzut możliwych wartości pędu będzie odpowiednio wielki, zgodnie z określonym przez Heisenberga związkiem. Iloczyn dwóch nieoznaczoności (możemy przypisać im wielkości liczbowe) będzie zawsze większy od wszechobecnej stałej Plancka. Zasada Heisenberga raz na zawsze usuwa klasyczne pojęcie orbity. Nawet samo pojęcie położenia czy prędkości stało się nieco mniej wyraźne. Wróćmy teraz do Newtona i czegoś, co potrafimy sobie unaocznić.
Przypuśćmy, że mamy prostą drogę, po której z przyzwoitą prędkością sunie toyota. Postanawiamy zmierzyć jej położenie w chwili, gdy przemyka obok nas. Chcemy też dowiedzieć się, jak szybko jedzie. w newtonowskiej fizyce określenie położenia i prędkości ciała w danym momencie pozwala dokładnie przewidzieć, gdzie ciało to znajdzie się w dowolnej chwili w przyszłości. Kiedy jednak będziemy gromadzili nasze linijki i stopery, flesze i aparaty fotograficzne, zauważamy, że im staranniej mierzymy położenie, tym bardziej maleje nasza zdolność do określenia prędkości i na odwrót. (Przypomnijmy, że prędkość jest miarą zmiany położenia podzielonej przez czas). Jednak w fizyce klasycznej możemy nieustannie doskonalić dokładność naszych pomiarów obu wielkości. Po prostu zwracamy się do jakiejś agencji rządowej z prośbą o większe fundusze i konstruujemy lepszą aparaturę.
Inaczej rzecz się przedstawia w świecie atomowym. Według postulatu Heisenberga mamy tam do czynienia z fundamentalną niepoznawalnością, której nie niweluje ani najlepsza aparatura, ani największa przemyślność, ani państwowe fundusze. Heisenberg zaproponował, aby uznać za fundamentalne prawo przyrody to, że iloczyn dwóch nieoznaczoności jest zawsze większy niż h . Choć może się to wydawać dziwne, istnieją solidne podstawy fizyczne dla tego twierdzenia. Spróbujmy na przykład określić położenie elektronu. Najpierw musimy go "zobaczyć". To znaczy trzeba odbić od niego światło - wiązkę fotonów. No dobrze. Już widzimy elektron. Znamy jego położenie w danym momencie. Ale foton odbijający się od elektronu wpływa na jego ruch. Jeden pomiar podważa drugi. w mechanice kwantowej pomiar w sposób nieunikniony wywołuje zmiany w mierzonym systemie, ponieważ mamy do czynienia z układami atomowymi, a narzędzia pomiaru, jakimi dysponujemy, nie mogą już być ani trochę mniejsze, delikatniejsze czy subtelniejsze. Atomy mają jedną dziesięciomiliardową część centymetra średnicy i ważą milionową część miliardowej miliardowej części grama, tak że nie trzeba wiele, by znacząco wpłynąć na ich stan. Natomiast w wypadku układu klasycznego można mieć pewność, że akt pomiaru w sposób co najwyżej zaniedbywalny wpływa na mierzony układ. Przypuśćmy, że chcemy zmierzyć temperaturę wody. Nie zmienimy temperatury jeziora, zanurzając w nim mały termometr. Ale włożenie wielkiego termometru do naparstka z wodą byłoby głupie, gdyż na pewno wpłynęłoby na temperaturę wody. Teoria kwantowa mówi, że musimy uwzględniać pomiar jako nieodłączną część układu atomowego. |