Zadanie

Zadanie. Relatywistyka.

Dwie cząstki o jednakowych prędkościach v = 0,75 c poruszają się po jednej prostej i padają na tarczę. Jedna z nich uderzyła w tarczę o s później niż druga. Obliczyć odległość między tymi cząstkami w locie w układzie odniesienia związanym z nimi.

Rozwiązanie

Rozwiązanie

Niech x₁ i x₂ oznaczają współrzędne cząstek w układzie odniesienia związanym z tarczą, natomiast x₁' i x₂' współrzędne cząstek u układzie odniesienia związanym z nimi.

Zgodnie z transformacją Lorentza:

Wówczas odległość między cząstkami w układzie odniesienia związanym z nimi:

(1)

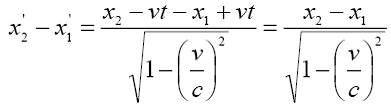
Odległość między cząstkami w układzie związanym z tarczą:

(2)

gdzie jest czasem zmierzonym pomiędzy uderzeniami cząstek o tarczę w układzie współrzędnych związanym z tarczą. Wstawiając (2) do (1) otrzymamy:

 

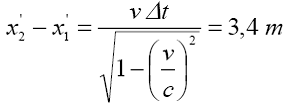
Odpowiedź

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Teoria Względności Alberta Einsteina

Na tropie wehikułu czasu

Teoria Względności a mechanika

Czas, odległość, teoria względności

Continuum czasoprzestrzenne

Czy czasoprzestrzeń jest euklidesowa?

Geometria przestrzeni

Linki

...

Zadania z przedmiotu

Zadania z relatywistyki