 Continuum
czasoprzestrzenne
Continuum
czasoprzestrzenne
"Poznałem
wspaniałą kobietę w Paryżu dnia 14 lipca 1995 roku".
W zdaniu tym określone zostały miejsce i czas zdarzenia.
Komuś, kto słyszałby to zdanie po raz pierwszy, a
nie wiedział, co znaczy słowo "Paryż", można
wytłumaczyć, że jest to miasto na kuli ziemskiej położone
pod 2° długości wschodniej i 49° szerokości północnej.
Tak więc dwie liczby charakteryzowałyby miejsce, w
którym zaszło zdarzenie, zaś "14 lipca 1995 roku"
- czas, w którym ono zaszło. Dokładne określenie,
gdzie i kiedy zaszło zdarzenie, jest w fizyce jeszcze
ważniejsze niż w historii, gdyż dane te stanowią podstawę
ilościowego opisu.
Dla
uproszczenia rozważaliśmy dotąd tylko ruchy wzdłuż
linii prostej. Naszym u. w. była sztywna sztaba mająca
początek, lecz nie mająca punktu końcowego. Utrzymajmy
nadal to ograniczenie. Weźmy pod uwagę różne punkty
na sztabie. Ich położenia można scharakteryzować jedną
tylko liczbą, współrzędną punktu. Powiedzenie, że
współrzędna punktu wynosi 7,586 metra, oznacza, że
punkt ten jest oddalony od początku sztaby o 7,586
metra. I na odwrót, jeśli ktoś poda mi dowolną liczbę
i jednostkę, zawsze mogę znaleźć na sztabie punkt
odpowiadający tej liczbie. Możemy stwierdzić: każdej
liczbie odpowiada określony punkt na sztabie, a każdemu
punktowi na sztabie odpowiada określona liczba. Matematycy
wyrażają ten fakt następującym zdaniem: wszystkie
punkty na sztabie tworzą jednowymiarowe continuum.
Dla każdego punktu na sztabie zawsze istnieje punkt
dowolnie bliski. Dwa odległe punkty na sztabie można
połączyć ze sobą, posuwając się dowolnie małymi odcinkami.
Możliwość łączenia odległych punktów za pomocą dowolnie
małych odcinków jest więc charakterystyczną cechą
continuum.
A
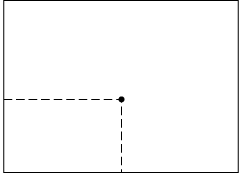
teraz inny przykład. Mamy płaszczyznę lub - jeśli
kto woli coś bardziej konkretnego - powierzchnię prostokątnego
stołu. Położenie punktu na tym stole może być scharakteryzowane
przez dwie liczby, a nie, jak uprzednio, przez jedną.
Te dwie liczby to odległości od dwóch prostopadłych
krawędzi stołu. Każdemu punktowi na płaszczyźnie odpowiada
nie jedna liczba, lecz para liczb; każdej parze liczb
odpowiada określony punkt. Innymi słowy: płaszczyzna
jest dwuwymiarowym continuum. Dla każdego
punktu na płaszczyźnie zawsze istnieją punkty dowolnie
bliskie. Dwa odległe punkty można połączyć krzywą,
dającą się podzielić na dowolnie małe odcinki. Tak
więc dowolna małość odcinków dających połączenie dwóch
odległych punktów, z których każdy może być przedstawiony
za pomocą dwóch liczb, jest znów charakterystyczną
cechą dwuwymiarowego continuum.
Jeszcze
jeden przykład. Wyobraźmy sobie, że chcemy uważać
nasz pokój za u. w. Znaczy to, że chcemy opisywać
wszystkie położenia w stosunku do sztywnych ścian
pokoju.
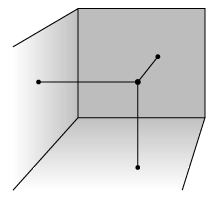
Położenie
końca lampy, jeśli lampa ta pozostaje w spoczynku,
można zapisać w formie trzech liczb: dwie z nich wyznaczają
odległość od dwóch prostopadłych ścian, trzecia -
odległość od podłogi lub sufitu. Każdemu punktowi
przestrzeni odpowiadają określone trzy liczby; każdym
trzem liczbom odpowiada określony punkt przestrzeni.
Wyrażamy to zdaniem: nasza przestrzeń jest trójwymiarowym
continuum. Dla każdego punktu przestrzeni istnieją
punkty dowolnie bliskie. I znów dowolna małość odcinków
dających połączenie odległych punktów, z których każdy
jest przedstawiony przez trzy liczby, jest charakterystyczną
cechą trójwymiarowego continuum.
Wszystko
to jednak ma niewiele wspólnego z fizyką. Aby powrócić
do fizyki, musimy rozważyć ruch cząstek materialnych.
Chcąc obserwować i przewidywać zdarzenia zachodzące
w przyrodzie, musimy brać pod uwagę nie tylko miejsce,
ale i czas, w którym zachodzą zdarzenia fizyczne.
Weźmy znów bardzo prosty przykład.
Z
wieży upuszczony zostaje mały kamień, który można
uważać za cząstkę. Przypuśćmy, że wysokość wieży wynosi
80 m. Od czasów Galileusza potrafimy przewidywać,
jaka będzie współrzędna kamienia w dowolnej chwili
po jego upuszczeniu. Oto "rozkład jazdy" opisujący
położenia kamienia po 0, 1, 2, 3 i 4 sekundach.
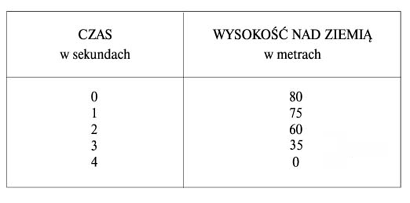
Nasz
"rozkład jazdy" notuje pięć zdarzeń, z których
każde przedstawione jest przez dwie liczby - współrzędną
czasową i przestrzenną danego zdarzenia. Pierwszym
zdarzeniem jest upuszczenie kamienia z wysokości 80
metrów nad ziemią w zerowej sekundzie. Drugim zdarzeniem
jest minięcie przez kamień kreski na naszej sztywnej
sztabie (wieża) na wysokości 75 metrów nad ziemią.
Następuje to po pierwszej sekundzie. Ostatnim zdarzeniem
jest zderzenie się kamienia z ziemią.
Wiadomości
uzyskane z naszego "rozkładu jazdy" możemy ująć
w nieco inny sposób. Pięć par liczb z "rozkładu
jazdy" możemy przedstawić jako pięć punktów na płaszczyźnie.
Najpierw ustalmy skalę. Jeden odcinek będzie odpowiadał
metrowi, drugi sekundzie. Na przykład:

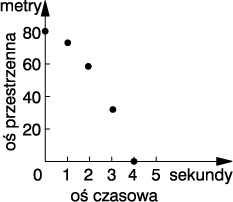
Następnie
narysujmy dwie prostopadłe linie i nazwijmy na przykład
poziomą - osią czasową, pionową zaś - osią przestrzenną.
Widać od razu, że nasz "rozkład jazdy" można
przedstawić w postaci pięciu punktów na płaszczyźnie
czasoprzestrzennej. Odległości punktów od osi przestrzennej
przedstawiają współrzędne czasowe, zanotowane w pierwszej
kolumnie naszego rozkładu jazdy", odległości od osi
czasowej oznaczają współrzędne przestrzenne.
Dokładnie
te same informacje można zapisać na dwa sposoby: za
pomocą "rozkładu jazdy" oraz za pomocą punktów
na płaszczyźnie. Każdy z tych zapisów można skonstruować
na podstawie znajomości drugiego. Wybór jednego z
tych dwóch sposobów jest wyłącznie sprawą gustu, gdyż
są one w gruncie rzeczy równoważne.
Pójdźmy
teraz o krok dalej. Wyobraźmy sobie lepszy "rozkład
jazdy", który by podawał położenie nie co sekundę,
lecz na przykład co jedną setną albo jedną tysięczną
sekundy. Na naszej płaszczyźnie czasoprzestrzennej
będziemy wtedy mieli bardzo wiele punktów.
Jeśli
wreszcie położenie będzie określone dla każdej chwili,
czyli, jak powiadają matematycy, jeśli współrzędna
przestrzenna będzie zadana jako funkcja czasu, wówczas
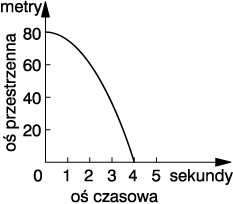
nasz układ punktów stanie się linią ciągłą. Następny
rysunek przedstawia więc pełną wiedzę o ruchu, a nie,
jak poprzednio, jej wycinek.
Ruch
wzdłuż sztywnej sztaby (wieży), ruch w przestrzeni
jednowymiarowej, jest tu przedstawiony w postaci krzywej
w dwuwymiarowym continuum czasoprzestrzennym. Każdemu
punktowi naszego continuum czasoprzestrzennego odpowiada
para liczb, z których jedna oznacza współrzędną czasową,
druga - współrzędną przestrzenną.
I
na odwrót: każdej parze liczb charakteryzującej zdarzenie
odpowiada określony punkt naszej płaszczyzny czasoprzestrzennej.
Dwa sąsiednie punkty przedstawiają dwa zdarzenia,
które zaszły w nieznacznie tylko odległych miejscach
i w nieznacznie odległych chwilach.
Mógłby
ktoś postawić naszemu ujęciu zarzut, że nie ma sensu
przedstawiać jednostki czasu w postaci odcinka, łączyć
ten odcinek mechanicznie z przestrzenią i tworzyć
z dwóch continuów jednowymiarowych jedno continuum
dwuwymiarowe. Taki sam zarzut trzeba by jednak postawić
wszystkim wykresom obrazującym na przykład zeszłoroczne
zmiany temperatury w Nowym Jorku lub wykresom przedstawiającym
zmiany kosztów utrzymania w ciągu ostatnich kilku
lat, w każdym z tych wypadków stosowano bowiem dokładnie
tę samą metodę. Na wykresach temperatury jednowymiarowe
continuum temperatury połączono z jednowymiarowym
continuum czasu w dwuwymiarowe continuum temperaturowo-czasowe.
Powróćmy
do cząstki upuszczonej z osiemdziesięciometrowej wieży.
Nasz graficzny obraz ruchu jest bardzo pożyteczny,
gdyż wyznacza on położenie cząstki w dowolnej chwili.
Wiedząc, jak się cząstka porusza, chcielibyśmy jeszcze
raz przedstawić jej ruch. Można tego dokonać na dwa
sposoby.
Pamiętamy
obraz cząstki zmieniającej w czasie swe położenie
w jednowymiarowej przestrzeni. Przedstawiamy tu ruch,
jako następstwo zdarzeń w jednowymiarowym continuum
przestrzennym. Nie mieszamy czasu i przestrzeni, stosujemy
obraz dynamiczny, w którym położenia
zmieniają się z upływem czasu.
Ale
ten sam ruch można przedstawić inaczej. Rozważając
krzywą w dwuwymiarowym continuum czasoprzestrzennym,
uzyskamy obraz statyczny. Ruch jest teraz
przedstawiony jako coś, co j e s t,
co istnieje w dwuwymiarowym continuum czasoprzestrzennym,
a nie jako coś, co się zmienia w jednowymiarowym continuum
przestrzennym.
Oba
te obrazy są ściśle równoważne i wybór jednego z nich
jest tylko rzeczą umowy i gustu.
Wszystko,
co powiedzieliśmy tu o dwóch obrazach ruchu, nie ma
absolutnie nic wspólnego z teorią względności. Każde
z tych przedstawień jest równie dobre, choć fizyka
klasyczna skłaniała się raczej ku obrazowi dynamicznemu,
opisującemu ruch jako coś dziejącego się w przestrzeni,
a nie jako coś istniejącego w czasoprzestrzeni. Teoria
względności zmieniła jednak ten pogląd. Wypowiedziała
się ona wyraźnie za obrazem statycznym, znajdując
w takim właśnie przedstawieniu ruchu, jako czegoś
istniejącego w czasoprzestrzeni, wygodniejszy i bardziej
obiektywny obraz rzeczywistości. Pozostaje nam jeszcze
odpowiedzieć na pytanie: dlaczego te dwa obrazy, równoważne
z punktu widzenia fizyki klasycznej, nie są równoważne
z punktu widzenia teorii względności"
Aby
zrozumieć odpowiedź na to pytanie, rozważmy znów dwa
u. w., poruszające się względem siebie ruchem jednostajnym.
Według
fizyki klasycznej obserwatorzy w dwóch u. w., poruszających
się względem siebie ruchem jednostajnym, przypiszą
danemu zdarzeniu różne współrzędne przestrzenne, ale
jednakową współrzędną czasową. Tak więc, w naszym
przykładzie, zderzenie cząstki z ziemią określone
jest w naszym wybranym u .w. przez współrzędną czasową
"4" oraz przez współrzędną przestrzenną "0".
Według mechaniki klasycznej obserwator poruszający
się względem wybranego u. w. ruchem jednostajnym też
stwierdzi, że kamień spadł na ziemię po czterech sekundach.
Obserwator ten będzie jednak odnosił odległość do
swego u. w. i przypisze zdarzeniu upadku na ogół inne
współrzędne przestrzenne, choć współrzędna czasowa
będzie taka sama dla niego, jak i dla wszystkich innych
obserwatorów poruszających się względem siebie ruchem
jednostajnym. Fizyka klasyczna zna tylko "bezwzględny"
bieg czasu dla wszystkich obserwatorów. W każdym u.
w. można rozbić continuum dwuwymiarowe na dwa continua
jednowymiarowe: czas i przestrzeń. Z uwagi na "bezwzględny"
charakter czasu, przejście od "statycznego" do
"dynamicznego" obrazu ruchu ma w fizyce klasycznej
obiektywny sens.
Daliśmy
się już jednak przekonać, że na ogół nie wolno w fizyce
stosować transformacji klasycznej. Z praktycznego
punktu widzenia można ją nadal stosować przy małych
prędkościach, ale nie można z jej pomocą rozwiązywać
podstawowych zagadnień fizyki.
Według
teorii względności czas zderzenia kamienia z ziemią
nie będzie dla wszystkich obserwatorów taki sam. Współrzędne
czasowe i współrzędne przestrzenne będą różne w dwóch
u. w., a zmiana współrzędnej czasowej będzie zupełnie
wyraźna, jeśli względna prędkość będzie bliska prędkości
światła. Nie można, jak w fizyce klasycznej, rozbić
continuum dwuwymiarowego na dwa continua jednowymiarowe.
Przy wyznaczaniu współrzędnych czasoprzestrzennych
w innym u. w. nie wolno nam rozważać oddzielnie czasu
i przestrzeni. Rozbijanie continuum dwuwymiarowego
na dwa jednowymiarowe wydaje się z punktu widzenia
teorii względności postępowaniem dowolnym, nie posiadającym
obiektywnego znaczenia.
Wszystko,
cośmy dotąd powiedzieli, łatwo jest uogólnić na przypadek
ruchu nie ograniczonego do linii prostej. Istotnie,
do opisu zdarzeń zachodzących w przyrodzie potrzeba
nie dwóch, lecz czterech liczb. Nasza przestrzeń fizyczna,
wyznaczona przez obiekty i ich ruch, ma trzy wymiary
i położenia określane są przez te liczby. Chwila,
w której zachodzi zdarzenie, jest czwartą liczbą.
Każdemu zdarzeniu odpowiadają cztery określone liczby;
każdej czwórce liczb odpowiada określone zdarzenie.
A więc: świat zdarzeń tworzy czterowymiarowe continuum.
Nie ma w tym nic tajemniczego i ostatnie zdanie jest
równie prawdziwe dla fizyki klasycznej, jak i dla
teorii względności. Różnica ujawnia się znów, gdy
rozpatrywać dwa u. w., które się względem siebie poruszają.
Pokój porusza się, a obserwatorzy, wewnętrzny i zewnętrzny,
wyznaczają współrzędne czasoprzestrzenne tych samych
zdarzeń. Fizyk klasyczny i tym razem rozbija czterowymiarowe
continua na trójwymiarowe przestrzenie i jednowymiarowe
continuum czasowe.
Dawny
fizyk zajmuje się tylko transformacjami przestrzennymi,
gdyż czas jest dla niego bezwzględny. Rozbijanie czterowymiarowych
continuów świata na przestrzeń i czas uważa on za
naturalne i wygodne. Ale z punktu widzenia teorii
względności przy przechodzeniu z jednego u. w. do
drugiego zmienia się nie tylko przestrzeń, ale i czas,
a transformacja Lorentza opisuje własności transformacyjne
czterowymiarowego continuum czasoprzestrzennego związanego
z naszym czterowymiarowym światem zdarzeń.
Świat
zdarzeń można opisać dynamicznie za pomocą obrazu
zmieniającego się w czasie i przedstawionego na tle
przestrzeni trójwymiarowej. Można go jednak również
opisać za pomocą obrazu statycznego, przedstawionego
na tle czterowymiarowego continuum czasoprzestrzennego.
Z punktu widzenia fizyki klasycznej oba obrazy, dynamiczny
i statyczny, są sobie równoważne. Ale z punktu widzenia
teorii względności obraz statyczny jest wygodniejszy
i bardziej obiektywny.
Obrazem
dynamicznym możemy, jeśli wolimy, posługiwać się nawet
w teorii względności. Musimy jednak pamiętać, że ten
podział na czas i przestrzeń nie ma sensu obiektywnego,
gdyż czas nie jest już "bezwzględny".
W
dalszych fragmentach będziemy nadal posługiwać się
językiem "dynamicznym", a nie statycznym, pamiętając
jednak o jego ograniczeniach. |