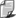 Geometria przestrzeni
Geometria przestrzeni
"czasoprzestrzeńń dyktuje masie jak się poruszać,
masa dyktuje czasoprzestrzeni jak się zakrzywiać"
Jaki jest związek ogólnej teorii względności z geometrią.
Zacznijmy od opisu świata, w którym żyją istoty nie, jak w naszym świecie, trójwymiarowe, lecz dwuwymiarowe. Kino przyzwyczaiło nas do dwuwymiarowych istot, działających na dwuwymiarowych ekranach. Wyobraźmy sobie teraz, że owe istoty-cienie, to znaczy aktorzy na ekranie, rzeczywiście istnieją, że posiadają zdolność myślenia, że mogą tworzyć swą własną naukę, że dwuwymiarowy ekran stanowi dla nich przestrzeń geometryczną. Istoty te nie są w stanie wyobrazić sobie w sposób namacalny przestrzeni trójwymiarowej, tak jak my nie potrafimy sobie wyobrazić świata czterowymiarowego. Potrafią zgiąć linię prostą i wiedzą, co to jest koło, ale nie mogą zbudować kuli, gdyż oznaczałoby to wyjście poza ich dwuwymiarowy ekran. Znajdujemy się w podobnym położeniu. Możemy zginać i zakrzywiać linie i powierzchnie, ale w żaden sposób nie potrafimy sobie wyobrazić zgiętej i zakrzywionej przestrzeni trójwymiarowej.
Żyjąc, myśląc i przeprowadzając doświadczenia, nasze istoty-cienie mogłyby z czasem opanować dwuwymiarową geometrię euklidesową. Mogłyby więc na przykład udowodnić, że suma kątów trójkąta wynosi 180 stopni. Mogłyby skonstruować dwa koła ze wspólnym środkiem, jedno bardzo małe, drugie duże. Stwierdziłyby, że stosunek obwodów takich dwóch okręgów jest równy stosunkowi ich promieni, co jest znów wynikiem charakterystycznym dla geometrii euklidesowej. Jeśliby ekran był nieskończenie duży, istoty-cienie stwierdziłyby, że wyruszywszy raz w podróż prosto przed siebie, nigdy nie wrócą do swego punktu wyjścia.
Wyobraźmy sobie teraz, że zmieniają się warunki, w których żyją nasze dwuwymiarowe istoty. Przypuśćmy, że ktoś z zewnątrz, z "trzeciego wymiaru", przenosi je z ekranu na powierzchnię kuli o bardzo dużym promieniu. Jeśli nasze cienie są bardzo małe w stosunku do całej powierzchni, jeśli nie mają środków porozumienia się na odległość i jeśli nie mogą podróżować zbyt daleko, nie zauważą żadnej zmiany. Suma kątów w małych trójkątach będzie nadal wynosiła 180 stopni. Stosunek obwodów dwóch małych okręgów będzie równy stosunkowi ich promieni. Podróż po linii prostej nie będzie nigdy prowadzić do punktu wyjścia.
Niech jednak istoty-cienie rozwiną z biegiem czasu swą wiedzę techniczną. Niech wynajdą środki komunikacji, które pozwolą im szybko pokonywać duże odległości. Stwierdzą wówczas, że podróżując prosto przed siebie, powrócą w końcu do punktu wyjścia. "Prosto przed siebie" znaczy teraz "po wielkim okręgu kuli". Stwierdzą również, iż stosunek obwodów dwóch okręgów ze wspólnym środkiem nie jest równy stosunkowi promieni, jeśli jeden promień jest mały, a drugi bardzo duży.
Jeśli nasze dwuwymiarowe istoty są konserwatywne, jeśli w ciągu wielu pokoleń, gdy nie umiały jeszcze daleko podróżować, uczyły się geometrii euklidesowej, która się wtedy dobrze zgadzała z obserwowanymi faktami, będą z pewnością robiły co w ich mocy, aby przy niej pozostać, wbrew świadectwu swoich pomiarów. Mogą próbować zrzucać winę za te rozbieżności na fizykę. Mogą poszukiwać fizycznych przyczyn odkształcania linii i powodujących odstępstwa od geometrii euklidesowej, przyczyn takich, jak na przykład różnice temperatury. Ale wcześniej czy później muszą zauważyć, że istnieje znacznie bardziej logiczny i przekonujący sposób opisu tych zjawisk. Z czasem zrozumieją, że ich świat jest skończony, że zasady jego geometrii są inne od tych, których się uczyły. Zrozumieją, że ich świat jest dwuwymiarową powierzchnią kuli, mimo że sobie tego nie będą mogły wyobrazić. Szybko nauczą się nowych zasad geometrii, które się wprawdzie różnią od euklidesowych, ale mimo to dają się sformułować dla ich dwuwymiarowego świata w sposób równie logiczny i konsekwentny. Nowe pokolenie, wychowane ze znajomością geometrii kuli, będzie uważało geometrię euklidesową za bardziej skomplikowaną i sztuczną, gdyż nie zgadza się ona z obserwowanymi faktami.
Powróćmy do trójwymiarowych istot naszego świata.
Co mamy na myśli mówiąc, że nasza trójwymiarowa przestrzeń ma charakter euklidesowy? Znaczy to, że wszystkie udowodnione logicznie twierdzenia geometrii euklidesowej można również potwierdzić faktycznym doświadczeniem. Za pomocą ciał sztywnych lub promieni świetlnych możemy konstruować obiekty odpowiadające wyidealizowanym obiektom geometrii euklidesowej. Krawędź linijki lub promień świetlny odpowiada linii prostej; suma kątów trójkąta zbudowanego z cienkich sztywnych prętów wynosi 180 stopni; stosunek skonstruowanych z cienkiego sztywnego drutu promieni dwóch kół o wspólnym środku jest równy stosunkowi obwodów tych kół. Geometria euklidesowa staje się w tej interpretacji działem fizyki, co prawda bardzo prostym.
Ale można sobie wyobrazić, że wykryto rozbieżności: na przykład suma kątów wielkiego trójkąta zbudowanego z prętów, które z rozmaitych powodów należy uważać za sztywne, okazała się różna od 180 stopni. Ponieważ przyzwyczailiśmy się już do poglądowego przedstawiania obiektów geometrii euklidesowej, używając ciał sztywnych, dopatrywalibyśmy się zapewne przyczyny takiego nieoczekiwanego zachowania się naszych prętów w działaniu jakiejś siły fizycznej. Próbowalibyśmy znaleźć charakter fizyczny tej siły oraz jej wpływ na inne zjawiska. Aby ocalić geometrię euklidesową, postawilibyśmy naszym przedmiotom zarzut, że nie są one sztywne, że nie odpowiadają dokładnie obiektom geometrii euklidesowej. Próbowalibyśmy lepiej przedstawiać te obiekty, aby zachowywały się one tak, jak przewiduje geometria euklidesowa. Jeśliby się nam jednak nie udało połączyć geometrii euklidesowej i fizyki w jeden prosty i konsekwentny obraz, musielibyśmy zrezygnować z przekonania, że nasza przestrzeń jest euklidesowa, i szukać bardziej przekonującego obrazu rzeczywistości, opartego na bardziej ogólnych założeniach co do geometrycznego charakteru naszej przestrzeni.
Potrzebę tego można zilustrować, posługując się wyidealizowanym doświadczeniem, wykazującym, że prawdziwie relatywistyczna fizyka nie może się opierać na geometrii euklidesowej. W naszym rozumowaniu będziemy korzystać z tego, co już wiemy o inercjalnym u. w. i o szczególnej teorii względności. Wyobraźmy sobie wielkie koło z narysowanymi na nim dwoma współśrodkowymi okręgami, jednym bardzo małym, drugim bardzo dużym. Koło wiruje szybko względem obserwatora zewnętrznego, a na kole znajduje się obserwator wewnętrzny. Zakładamy ponadto, że u. w. obserwatora zewnętrznego jest układem inercjalnym. Obserwator zewnętrzny może w swoim u. w. narysować te same dwa okręgi, mały i duży, spoczywające w jego u. w., lecz pokrywające się z okręgami na wirującym kole. Ponieważ jego u. w. jest inercjalny, obowiązuje w nim geometria euklidesowa, a więc obserwator zewnętrzny stwierdzi, że stosunek obwodów jest równy stosunkowi promieni. A co powie obserwator na kole? Z punktu widzenia fizyki klasycznej, a także szczególnej teorii względności, jego u.w. jest układem niedozwolonym.
Jeśli jednak chcemy znaleźć dla praw fizycznych nowe sformułowania, obowiązujące w dowolnym u. w., musimy obu obserwatorów, na kole i zewnętrznego, traktować z równą uwagą. Śledzimy teraz z zewnątrz poczynania obserwatora wewnętrznego, który stara się zmierzyć obwody i promienie na wirującym kole. Posługuje się on tym samym krótkim prętem mierniczym, którego używał obserwator zewnętrzny. "Ten sam" oznacza albo rzeczywiście ten sam pręt, przekazany przez obserwatora zewnętrznego wewnętrznemu, albo jeden z dwóch prętów mających w spoczynku tę samą długość.
Obserwator wewnętrzny na kole zaczyna mierzyć promień i obwód małego okręgu. Wynik, który uzyska, powinien być taki sam, jak wynik obserwatora zewnętrznego. Oś, wokół której koło wiruje, przechodzi przez jego środek. Części koła położone blisko środka mają bardzo małe prędkości. Jeśli tylko okręg jest dostatecznie mały, możemy śmiało stosować mechanikę klasyczną, zaniedbując szczególną teorię względności. Znaczy to, że długość pręta jest dla obserwatora zewnętrznego i wewnętrznego taka sama i że wyniki tych dwóch pomiarów będą dla nich obu jednakowe. Teraz obserwator na kole mierzy promień dużego okręgu. Pręt umieszczony wzdłuż promienia porusza się względem obserwatora zewnętrznego. Ponieważ jednak kierunek ruchu jest prostopadły do pręta, nie kurczy się on i będzie miał dla obu obserwatorów taką samą długość. Mamy więc trzy pomiary, które dadzą dla obu obserwatorów taki sam wynik: dwa promienie i mały obwód. Ale z czwartym pomiarem rzecz się ma inaczej! Długość dużego obwodu będzie dla każdego z obu obserwatorów inna. Pręt umieszczony na obwodzie zgodnie z kierunkiem ruchu będzie się obserwatorowi zewnętrznemu wydawał skrócony w stosunku do jego spoczywającego pręta. Prędkość jest teraz znacznie większa od prędkości małego okręgu i trzeba to skrócenie uwzględnić. Stosując wyniki szczególnej teorii względności, dochodzimy do wniosku: długość dużego obwodu wypadnie w pomiarach każdego z obu obserwatorów inaczej. Ponieważ tylko jedna spośród czterech zmierzonych przez obu obserwatorów długości nie jest dla nich jednakowa, zatem dla obserwatora wewnętrznego stosunek dwóch promieni nie może być równy stosunkowi dwóch obwodów, jak to jest dla obserwatora zewnętrznego. Znaczy to, że obserwator na kole nie może w swoim u. w. potwierdzić ważności geometrii euklidesowej.
Otrzymawszy ten wynik, obserwator na kole mógłby powiedzieć, że nie chce się zajmować u. w., w których nie obowiązuje geometria euklidesowa. Geometria ta zawiodła z powodu bezwzględnego ruchu wirowego, zawiodła, gdyż jego u. w. jest zły i niedozwolony. Ale rozumując w ten sposób, odrzuca on zasadniczą ideę ogólnej teorii względności. Z drugiej strony, jeśli chcemy odrzucić ruch bezwzględny i zachować ideę ogólnej teorii względności, to trzeba zbudować całą fizykę w oparciu o geometrię ogólniejszą od euklidesowej. Jest to nieuniknionym następstwem założenia, że dozwolone mają być wszystkie u. w.
Zmiany, które wprowadza ogólna teoria względności, nie mogą się ograniczać do samej tylko przestrzeni. W szczególnej teorii względności mieliśmy w każdym u. w. spoczywające w nim zegary, które miały ten sam rytm i były zsynchronizowane, to znaczy wskazywały jednocześnie ten sam czas. Co się dzieje z zegarem w nieinercjalnym u. w.? Posłużymy się znów naszym wyidealizowanym doświadczeniem z kołem. Obserwator zewnętrzny ma w swym inercjalnym u .w. doskonałe zegary, wszystkie o tym samym rytmie i wszystkie zsynchronizowane. Obserwator wewnętrzny bierze dwa takie same zegary i umieszcza jeden z nich na małym okręgu wewnętrznym, drugi na dużym zewnętrznym. Zegar na okręgu wewnętrznym ma względem obserwatora zewnętrznego bardzo małą prędkość. Możemy więc śmiało powiedzieć, że jego rytm będzie taki sam, jak rytm zegara na zewnątrz. Ale zegar na dużym okręgu ma znaczną prędkość, która sprawia, że zmienia się jego rytm w porównaniu z zegarami zewnętrznymi, a więc również w porównaniu z zegarem umieszczonym na małym okręgu. Dwa wirujące zegary będą więc miały różny rytm i nawiązując do wyników szczególnej teorii względności, znów widzimy, że w naszym wirującym u. w. nie można wprowadzać urządzeń takich, jak w inercjalnym u. w.
Aby wyjaśnić, jakie wnioski można wyciągnąć z tego i z poprzednio opisanych wyidealizowanych doświadczeń, przytoczmy raz jeszcze dialog pomiędzy dawnym fizykiem D, wierzącym w fizykę klasyczną, a fizykiem współczesnym W, który zna ogólną teorię względności. D jest obserwatorem zewnętrznym w inercjalnym u. w., podczas gdy W znajduje się na wirującym kole.
D. W twoim u. w. nie obowiązuje geometria euklidesowa. Śledziłem twoje pomiary i zgadzam się, że stosunek dwóch obwodów nie jest w twoim u. w. równy stosunkowi promieni. Ale świadczy to tylko o tym, że twój u. w. jest niedozwolony. Tymczasem mój u. w. ma charakter inercjalny i mogę śmiało stosować geometrię euklidesową. Twoje koło pozostaje w ruchu bezwzględnym i z punktu widzenia fizyki klasycznej stanowi niedozwolony u. w., w którym nie obowiązują prawa mechaniki.
W. Nie chcę nic słyszeć o ruchu bezwzględnym. Mój u. w. jest równie dobry, jak twój. Zauważyłem tylko, że ty się obracasz wokół mojego koła. Nikt mi nie zabroni odnosić ruchów do mojego koła.
D. Lecz czy nie czułeś dziwnej siły starającej się odrzucić cię od środka koła? Gdyby twoje koło nie było szybko wirującą karuzelą, dwa fakty, które zaobserwowałeś, z pewnością nie miałyby miejsca: nie spostrzegłbyś siły ciągnącej cię na zewnątrz, ani nie stwierdziłbyś, że w twoim u. w. nie można stosować geometrii euklidesowej. Czy fakty te nie wystarczają, aby cię przekonać, że twój u. w. pozostaje w ruchu bezwzględnym?
W. Bynajmniej! Oczywiście, zauważyłem oba fakty, o których mówisz, ale uważam, że ich przyczyną jest pewne dziwne pole grawitacyjne, działające na moje koło. Pole to jest skierowane na zewnątrz koła i odkształca moje pręty oraz zmienia rytm moich zegarów. Pole grawitacyjne, geometria nieeuklidesowa, zegary o różnych rytmach - wszystko to jest moim zdaniem ściśle z sobą związane. Przyjmując jakiś u. w., muszę jednocześnie założyć istnienie odpowiedniego pola grawitacyjnego, działającego na sztywne pręty i zegary.
D. Ale czy zdajesz sobie sprawę z trudności, jakie pociąga za sobą twoja ogólna teoria względności? Wyjaśnię, o co mi chodzi, na prostym przykładzie spoza fizyki. Wyobraź sobie wyidealizowane miasto amerykańskie składające się z siatki równoległych ulic i prostopadłych do nich, równoległych alei. Odległości między ulicami, a także między alejami są wszędzie jednakowe. Przy takim założeniu wszystkie bloki są dokładnie takich samych rozmiarów. W ten sposób mogę łatwo określić położenie każdego bloku. Taka konstrukcja byłaby jednak niemożliwa bez geometrii euklidesowej. Nie możemy więc na przykład pokryć całej naszej Ziemi jednym ogromnym wyidealizowanym miastem amerykańskim. Przekona cię o tym rzut oka na globus. Ale taką "siatką amerykańskiego miasta" nie moglibyśmy również pokryć twego koła. Twierdzisz, że pole grawitacyjne odkształca twoje pręty. Fakt, że nie udało ci się sprawdzić twierdzenia Euklidesa o równości stosunków promieni i obwodów, wskazuje wyraźnie, że jeśli zechcesz konstruować taką siatkę ulic i alei na dostatecznie dużym obszarze, prędzej czy później natkniesz się na trudności i stwierdzisz, że jest to na twoim kole niemożliwe. Geometria na twym wirującym kole przypomina geometrię na zakrzywionej powierzchni, gdzie oczywiście skonstruowanie na dostatecznie dużej części powierzchni siatki ulic i alei jest niemożliwe. Innym, bardziej fizycznym przykładem może być płaszczyzna ogrzana w sposób nierównomierny, tak że temperatury są w różnych częściach powierzchni inne. Czy mógłbyś za pomocą pręcików żelaznych wydłużających się pod wpływem temperatury skonstruować siatkę "równoległo-prostopadłą", którą poniżej narysowałem? Oczywiście nie! Twoje "pole grawitacyjne" płata twym sztabom takie same figle, jak zmiany temperatury pręcikom żelaznym.
W. Wszystko to mnie nie przeraża. Siatka ulic i alei potrzebna jest do wyznaczania położeń punktów, przy czym zegar porządkuje zdarzenia. Miasto nie musi być amerykańskie, równie dobrze może to być starożytne miasto europejskie. Wyobraź sobie, że twoje wyidealizowane miasto zostało wykonane z plasteliny, a następnie odkształcone. Nadal mogę numerować bloki i identyfikować ulice oraz aleje, choć nie są one już ani proste, ani równoległe. Podobnie długość i szerokość geograficzną wyznaczają położenia punktów na Ziemi, choć nie ma siatki "miasta amerykańskiego".
D. Mimo to widzę jednak trudność. Zmuszony jesteś stosować "siatkę miasta europejskiego".
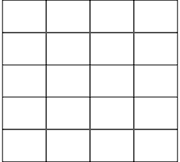
Zgadzam się, że możesz porządkować punkty lub zdarzenia, ale taka siatka wprowadzi ci bałagan do wszelkich pomiarów odległości. Nie da ci ona właściwości metrycznych przestrzeni, które daje moja siatka. Weź taki przykład. Wiem, że w moim mieście amerykańskim, aby przejść dziesięć bloków, muszę przebyć odległość równą podwojonej długości pięciu bloków. Ponieważ wiem, że wszystkie bloki są równe, mogę z łatwością wyznaczać odległości.
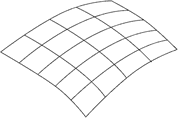
W. To prawda. W mojej siatce "miasta europejskiego" nie mogę mierzyć odległości bezpośrednio liczbą odkształconych bloków. Muszę wiedzieć coś ponadto; muszę znać własności geometryczne mojej powierzchni. Każdy wie przecież, że odległość między 0° i 10° długości na równiku nie jest taka sama, jak między 0° i 10° długości w pobliżu bieguna północnego. Ale każdy żeglarz wie, jak ocenić odległość między takimi dwoma punktami kuli ziemskiej, zna bowiem własności geometryczne Ziemi. Może on tę odległość wyznaczyć albo drogą obliczeń opartych na znajomości trygonometrii sferycznej, albo doświadczalnie, przepływając statkiem obie drogi z taką samą prędkością. W twoim przypadku całe zagadnienie jest banalne, gdyż wszystkie ulice i aleje są od siebie nawzajem jednakowo odległe. W przypadku Ziemi sprawa się komplikuje; południki 0° i 10° schodzą się na biegunach Ziemi, a na równiku odległość ich jest największa. Podobnie ja, aby wyznaczać odległości, muszę o mojej "siatce miasta europejskiego" wiedzieć coś więcej niż ty o twojej "siatce miasta amerykańskiego". Tę dodatkową wiedzę mogę zdobyć, badając w każdym szczególnym przypadku własności geometryczne mojego continuum.
D. Ale to wszystko wskazuje tylko, do jakich niewygód i komplikacji prowadzi wyrzeczenie się prostej struktury geometrii euklidesowej na rzecz złożonego schematu, który musisz stosować. Czy to naprawdę konieczne?
W. Obawiam się, że tak, jeśli chcemy stosować naszą fizykę w dowolnym u. w., bez uciekania się do tajemniczego układu inercjalnego. Zgadzam się, że stosowane przeze mnie narzędzie matematyczne jest bardziej złożone niż twoje, ale moje założenia fizyczne są prostsze i bardziej naturalne.
Dyskusja ta ograniczała się do continuów dwuwymiarowych. W ogólnej teorii względności sprawa jest jeszcze bardziej złożona, gdyż mamy tam nie dwuwymiarowe, lecz czterowymiarowe continuum czasoprzestrzenne. Ale idea jest taka sama jak w przypadku dwuwymiarowym. W ogólnej teorii względności nie możemy, jak w teorii szczególnej, stosować mechanicznego rusztowania złożonego z równoległych, prostopadłych sztab i zsynchronizowanych zegarów. Nie możemy w dowolnym u. w. wyznaczyć za pomocą sztywnych sztab i dobrze chodzących zsynchronizowanych zegarów punktu i chwili, w których zachodzi zdarzenie - jak to czyniliśmy w inercjalnym u. w. szczególnej teorii względności. Nadal możemy porządkować zdarzenia za pomocą naszych nieeuklidesowych sztab i różnie chodzących zegarów. Ale właściwe pomiary, wymagające sztywnych sztab oraz doskonale rytmicznych i zsynchronizowanych zegarów, można przeprowadzać tylko w u. w. lokalnie inercjalnym. Ważna w nim jest cała szczególna teoria względności, lecz nasz "dobry" u. w. jest tylko lokalny, jego inercjalny charakter jest ograniczony w przestrzeni i w czasie. Nawet w naszym dowolnym u. w. możemy przewidzieć wyniki pomiarów dokonanych w lokalnie inercjalnym u. w. W tym celu musimy jednak znać charakter geometryczny continuum czasoprzestrzennego.
Nasze wyidealizowane doświadczenia zarysowują tylko ogólny charakter nowej, relatywistycznej fizyki. Wskazują one, że zagadnieniem podstawowym jest zagadnienie ciążenia. Wskazują również, że ogólna teoria względności prowadzi do dalszego uogólnienia pojęć czasu i przestrzeni. |