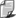Czas, odległość, teoria względności

Oto nasze założenia:

(1) Prędkość światła w próżni jest jednakowa we wszystkich u. w. poruszających się względem siebie ruchem jednostajnym.

(2) Wszystkie prawa przyrody są jednakowe we wszystkich u. w. poruszających się względem siebie ruchem jednostajnym.

Te dwa założenia są punktem wyjścia teorii względności. Nie będziemy się już odtąd posługiwali transformacją klasyczną, gdyż, jak wiemy, pozostaje ona w sprzeczności z naszymi założeniami.

Niezwykle ważne jest tu, jak wszędzie w nauce, uwolnienie się od głęboko zakorzenionych i często bezkrytycznie powtarzanych uprzedzeń. Ponieważ przekonaliśmy się, że zmiany w (1) i (2) prowadzą do sprzeczności z doświadczeniem, musimy mieć odwagę wyraźnego stwierdzenia ich słuszności i zaatakowania jedynego możliwego słabego punktu - sposobu, w jaki położenia i prędkości transformują się przy przejściu od jednego układu do drugiego. Będziemy chcieli wyciągnąć wnioski z (1) i (2), zobaczyć, gdzie i jak wnioski te są sprzeczne z transformacją klasyczną, oraz znaleźć sens fizyczny otrzymanych wyników.

Jeszcze raz posłużymy się przykładem poruszającego się pokoju, opisywanego przez obserwatora zewnętrznego i wewnętrznego. Znów ze środka pokoju zostaje wysłany sygnał świetlny i znów pytamy obu obserwatorów, co spodziewają się zaobserwować, przyjmując tylko nasze dwie zasady i zapominając, co się poprzednio mówiło o ośrodku, w którym się rozchodzi światło. Przytaczamy ich odpowiedzi:

Obserwator wewnętrzny: Sygnał świetlny biegnący ze środka pokoju dojdzie do wszystkich ścian r ó w n o c z e ś n i e, gdyż wszystkie one są jednakowo odległe od środka pokoju, a prędkość światła jest we wszystkich kierunkach jednakowa.

Obserwator zewnętrzny: Prędkość światła w moim układzie jest dokładnie taka sama, jak w układzie obserwatora poruszającego się wraz z pokojem. Nic mnie nie obchodzi, czy źródło światła porusza się w moim u. w., czy nie, gdyż jego ruch nie wpływa na prędkość światła. Ja widzę tylko sygnał świetlny biegnący z normalną prędkością, jednakową we wszystkich kierunkach. Jedna ściana stara się uciec przed tym sygnałem, druga stara się do niego zbliżyć. Toteż sygnał dojdzie do ściany uciekającej trochę później niż do zbliżającej się. Choć różnica - w przypadku, gdy prędkość pokoju jest mała w porównaniu z prędkością światła - będzie bardzo nieznaczna, to jednak sygnał świetlny nie dotrze do obu ścian prostopadłych do kierunku ruchu zupełnie jednocześnie.

Porównując przewidywania obu naszych obserwatorów, dochodzimy do wniosku, który pozostaje w jawnej sprzeczności z na pozór dobrze ugruntowanymi pojęciami fizyki klasycznej. Dwa zdarzenia, to jest dojście dwóch promieni świetlnych do dwóch ścian, są równoczesne dla obserwatora wewnętrznego, ale nie są równoczesne dla obserwatora zewnętrznego. W fizyce klasycznej mieliśmy jeden zegar, jeden bieg czasu dla wszystkich obserwatorów w każdym u. w. Czas, a więc i pojęcia takie, jak "jednocześnie", "wcześniej", "później", miały sens absolutny, niezależny od wyboru u. w. Dwa zdarzenia, które zaszły jednocześnie w pewnym u. w., musiały zajść jednocześnie również w każdym innym u. w.

Założenia (1) i (2), to znaczy teoria względności, zmuszają nas do odstąpienia od tego poglądu. Opisaliśmy dwa zdarzenia, które w jednym u. w. zachodzą w tym samym czasie, a w innym u. w. w różnych czasach. Chodzi teraz o to, aby ten fakt zrozumieć, aby uświadomić sobie sens zdania: "Dwa zdarzenia, które są jednoczesne w jednym u. w., mogą nie być jednoczesne w innym u. w.".

Co rozumiemy przez "dwa zdarzenia jednoczesne w pewnym u. w."? Sens tego pojęcia wydaje się dla każdego intuicyjnie zrozumiały. Postanówmy jednak być ostrożni i starajmy się podawać ścisłe określenia, wiemy bowiem, jak łatwo można przecenić intuicję. Przede wszystkim odpowiedzmy na proste pytanie.

Co to jest zegar?

Prymitywne, subiektywne poczucie upływu czasu pozwala nam porządkować nasze wrażenia, stwierdzać, że jedno zdarzenie zachodzi wcześniej, inne później. Do tego jednak, by wykazać, że odstęp czasowy między dwoma zdarzeniami wynosi 10 sekund, potrzebny jest zegar. Użycie zegara sprawia, że pojęcie czasu staje się obiektywne. Za zegar może służyć dowolne zjawisko fizyczne pod warunkiem, że można je powtarzać dowolnie wiele razy. Przyjmując za jednostkę czasu odstęp między początkiem i końcem takiego zjawiska, można, powtarzając nasz proces fizyczny, mierzyć dowolne odstępy czasu. Jest to zasada, na której opierają się wszystkie zegary, od prostej klepsydry do najsubtelniejszych przyrządów. W przypadku klepsydry jednostką czasu jest odstęp, w którym piasek przesypuje się z górnego naczynia do dolnego. Ten sam proces fizyczny można powtórzyć, odwracając naczynie.

Mamy dwa doskonałe zegary umieszczone w dwóch odległych punktach i wskazujące dokładnie ten sam czas. Twierdzenie to powinno być prawdziwe bez względu na to, jak dokładnie je sprawdzamy. Cóż ono jednak właściwie oznacza? W jaki sposób możemy się upewnić, że odległe zegary zawsze wskazują dokładnie ten sam czas? Można by się w tym celu posłużyć telewizją. Oczywiście telewizja jest tu użyta tylko jako przykład i nie ma istotnego znaczenia dla naszego rozumowania. Mógłbym stanąć przy jednym z zegarów i obserwować obraz telewizyjny drugiego. Mógłbym wtedy stwierdzić, czy wskazują one jednocześnie ten sam czas. Nie byłby to jednak dobry sprawdzian. Obraz telewizyjny jest przenoszony za pośrednictwem fal elektromagnetycznych, a więc biegnie z prędkością światła. Obraz, który widzę na ekranie telewizyjnym, został wysłany przed pewnym - bardzo krótkim - czasem, podczas gdy to, co widzę na prawdziwym zegarze, dzieje się w tej chwili. Trudności tej można łatwo uniknąć. Muszę wziąć obrazy telewizyjne obu zegarów w punkcie jednakowo odległym od każdego z nich i obserwować je z tego środkowego punktu. Wówczas, jeśli oba sygnały były wysłane jednocześnie, dojdą do mnie w tej samej chwili. Jeżeli dwa dobre zegary, obserwowane ze środka łączącego je odcinka, zawsze wskazują ten sam czas, to nadają się one do wyznaczania czasu zdarzeń w dwóch odległych punktach.

W mechanice używaliśmy tylko jednego zegara. Nie było to zbyt wygodne, gdyż wszystkie pomiary trzeba było wykonywać w pobliżu tego jednego zegara. Obserwując zegar na odległość, na przykład przez telewizję, trzeba zawsze pamiętać, że to, co widzimy teraz, w rzeczywistości zaszło wcześniej, podobnie jak patrząc na zachód słońca, dostrzegamy to zdarzenie z ośmiominutowym opóźnieniem. Przy wszelkim odczytywaniu czasu trzeba wprowadzać poprawki zależne od naszej odległości od zegara.

Dlatego niewygodnie mieć tylko jeden zegar. Skoro jednak już wiemy, jak stwierdzić, czy dwa lub więcej zegarów wskazują jednocześnie ten sam czas i chodzą tak samo, możemy sobie świetnie wyobrazić w danym u. w. tyle zegarów, ile nam się podoba. Każdy z nich pozwoli nam wyznaczać czas zdarzeń zachodzących w jego bezpośrednim sąsiedztwie. Wszystkie zegary pozostają w spoczynku względem naszego u. w. Są to zegary "dobre" i zsynchronizowane, co znaczy, że wskazują jednocześnie ten sam czas.

W naszym zegarowym urządzeniu nie ma nic szczególnie dziwnego lub uderzającego. Zamiast jednego tylko zegara, używamy teraz wielu zsynchronizowanych, co pozwala łatwo stwierdzić, czy dwa odległe zdarzenia są w danym u. w. jednoczesne, czy nie. Zdarzenia te są jednoczesne, jeśli znajdujące się w ich pobliżu zsynchronizowane zegary wskazują w chwili ich zajścia ten sam czas. Powiedzenie, że jedno z odległych zdarzeń zachodzi wcześniej niż drugie, ma teraz w pełni określone znaczenie. Fakt taki można stwierdzić za pomocą spoczywających w naszym u. w. synchronizowanych zegarów.

Wszystko to jest zgodne z fizyką klasyczną i jak dotąd nie mamy żadnej sprzeczności z transformacją klasyczną.

W celu określenia równoczesności zdarzeń trzeba zegary zsynchronizować za pomocą sygnałów. Jest rzeczą w naszym rozumowaniu bardzo istotną, że sygnały te biegną z prędkością światła - z prędkością, która w teorii względności odgrywa tak podstawową rolę.

Ponieważ chcemy się zająć ważnym problemem dwóch u. w., poruszających się względem siebie ruchem jednostajnym, musimy wziąć dwie sztaby, z których każda zaopatrzona jest w zegary. Obserwator w każdym z dwóch poruszających się względem siebie u. w. ma teraz swą własną sztabę wraz ze związanym z nią układem zegarów.

Rozpatrując pomiary w mechanice klasycznej, używaliśmy dla wszystkich u. w. jednego zegara. Teraz w każdym u. w. mamy wiele zegarów. Różnica ta nie ma znaczenia. Wystarczyłby i jeden zegar, ale w mechanice klasycznej nikt nie mógł mieć nic przeciw użyciu wielu zegarów, dopóki zachowywały się one jak przystoi przyzwoitym zsynchronizowanym zegarom.

Zbliżamy się teraz do zasadniczego punktu, wskazującego, w którym miejscu transformacja klasyczna przeczy teorii względności. Co się dzieje, gdy dwa układy zegarów poruszają się względem siebie ruchem jednostajnym? Fizyk klasyczny odpowiedziałby: Nic - mają one nadal ten sam rytm i do wyznaczania czasu możemy używać zarówno zegarów poruszających się, jak spoczywających. Według fizyki klasycznej dwa zdarzenia równoczesne w jednym u. w., będą równoczesne również w każdym innym u. w.

Nie jest to jednak jedyna możliwa odpowiedź. Równie dobrze możemy sobie wyobrazić, że rytm zegara poruszającego się jest inny niż spoczywającego. Rozpatrzmy tę możliwość, nie przesądzając na razie, czy poruszające się zegary naprawdę zmieniają swój rytm. Co należy rozumieć przez powiedzenie, że poruszający się zegar zmienia swój rytm? Załóżmy dla uproszczenia, że w górnym u. w. mamy tylko jeden zegar, a w dolnym jest ich wiele. Wszystkie zegary mają taki sam mechanizm, przy czym dolne są zsynchronizowane, to znaczy wskazują równocześnie ten sam czas. Narysowaliśmy trzy następujące po sobie położenia obu poruszających się względem siebie u. w. Na pierwszym rysunku położenie wskazówek górnego i dolnych zegarów są jednakowe, tak bowiem umówiliśmy się je ustawić. Wszystkie zegary wskazują ten sam czas. Na drugim rysunku widzimy względne położenia obu u. w. po pewnym czasie. Wszystkie zegary w dolnym u. w. wskazują jednakowy czas, ale zegar w górnym u. w. spóźnia się. Rytm jego zmienił się i zachodzi różnica wskazań, gdyż porusza się on względem dolnego u. w. Na trzecim rysunku widzimy, jak z upływem czasu różnica położeń wskazówek rośnie.

Obserwator spoczywający w dolnym u. w. stwierdziłby, że poruszający się zegar zmienia rytm. Oczywiście ten sam wynik można by otrzymać, gdyby zegar poruszał się względem obserwatora spoczywającego w górnym u. w., musiałoby wtedy być wiele zegarów w górnym u. w. i tylko jeden w dolnym. Prawa przyrody muszą być takie same w obu poruszających się względem siebie u. w. W mechanice klasycznej zakładano milcząco, że poruszający się zegar nie zmienia rytmu. Wydawało się to tak oczywiste, że nawet o tym nie wspominano. Ale nic nie powinno być zbyt oczywiste; jeśli chcemy być naprawdę ostrożni, musimy zanalizować założenia, które dotąd przyjmowano w fizyce bez zastrzeżeń. Nie wolno odrzucać założenia tylko dlatego, że nie zgadza się ono z fizyką klasyczną. Można sobie doskonale wyobrazić, że poruszający się zegar zmienia swój rytm, jeśli tylko prawo określające tę zmianę jest jednakowe dla wszystkich inercjalnych u. w. A oto jeszcze jeden przykład. Weźmy miarkę metrową w postaci pręta; oznacza to, że nasz pręt, dopóki spoczywa w danym u. w., ma długość jednego metra. Z kolei pręt ten porusza się ruchem jednostajnym, przesuwając się wzdłuż sztaby przedstawiającej u. w. Czy długość jego będzie w dalszym ciągu wynosiła jeden metr? Musimy najpierw wiedzieć, w jaki sposób wyznaczyć tę długość. Dopóki pręt spoczywał, końce jego pokrywały się z odległymi o metr kreskami na podziałce u. w. 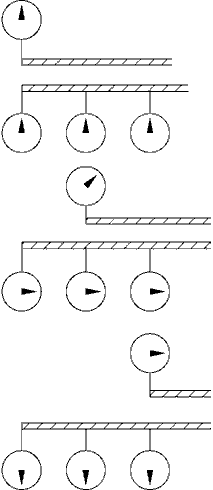Wnioskowaliśmy stąd, że długość spoczywającego pręta wynosi jeden metr. Jak mierzyć ten pręt w ruchu? Można by to zrobić w następujący sposób. W określonej chwili dwóch obserwatorów wykonuje jednocześnie zdjęcia migawkowe - jeden początku pręta, drugi jego końca. Ponieważ zdjęcia zostają wykonane równocześnie, możemy porównać kreski na sztabie u. w., z którymi pokrywa się początek i koniec poruszającego się pręta. W ten sposób wyznaczamy jego długość.

Potrzebni są dwaj obserwatorzy, którzy muszą uchwycić równoczesne zdarzenia zachodzące w różnych częściach danego u. w. Nic nie wskazuje na to, by wynik takich pomiarów miał być taki sam, jak w przypadku spoczywającego pręta. Ponieważ zdjęcia trzeba było wykonać równocześnie, co - jak już wiemy - jest pojęciem względnym, zależnym od u. w., wydaje się zupełnie możliwe, że wyniki tego pomiaru będą różne w rozmaitych poruszających się względem siebie u. w. Można sobie doskonale wyobrazić nie tylko to, że poruszający się zegar zmienia swój rytm, ale również, że poruszający się pręt zmienia swą długość, jeśli tylko prawa określające te zmiany są jednakowe dla wszystkich inercjalnych u. w.

Omówiliśmy kilka nowych możliwości, nie uzasadniając celowości ich przyjęcia.

Pamiętamy: prędkość światła jest taka sama we wszystkich inercjalnych u. w. Faktu tego nie można pogodzić z transformacją klasyczną. Ten krąg trzeba gdzieś przerwać. Czy nie można tego uczynić właśnie w tym miejscu? Czy nie możemy założyć takich zmian w rytmie poruszającego się zegara i w długości poruszającej się sztaby, żeby z tych założeń wynikała od razu stałość prędkości światła? Możemy! Jest to pierwszy przypadek, w którym teoria względności i fizyka klasyczna zasadniczo się różnią. Rozumowanie nasze można odwrócić: jeśli prędkość światła jest we wszystkich u. w. jednakowa, to poruszające się pręty muszą zmieniać swą długość, poruszające się zegary swój rytm, a prawa rządzące tymi zmianami są ściśle wyznaczone.

W tym wszystkim nie ma nic tajemniczego ani nierozsądnego. W fizyce klasycznej zawsze zakładano, że zegary w ruchu i w spoczynku mają taki sam rytm, że sztaby w ruchu i w spoczynku mają taką samą długość. Jeśli prędkość światła jest we wszystkich u. w. jednakowa, jeśli słuszna jest teoria względności, to z założenia tego trzeba zrezygnować. Trudno jest się wyzbyć głęboko zakorzenionych uprzedzeń, ale nie ma innego wyjścia. Z punktu widzenia teorii względności stare pojęcia wydają się dowolne. Dlaczego mielibyśmy wierzyć, jak to czyniliśmy jeszcze niedawno, w bezwzględny czas, płynący jednakowo dla wszystkich obserwatorów we wszystkich u. w.? Dlaczego mamy wierzyć w niezmienną odległość? Czas wyznacza się, używając zegarów, współrzędne przestrzenne za pomocą sztab, a wynik pomiaru może zależeć od zachowania się tych zegarów i sztab podczas ruchu. Nie ma powodu, by sądzić, że będą się one zachowywały tak, jak byśmy sobie tego życzyli. Obserwacja wykazuje pośrednio, poprzez zjawiska pola elektromagnetycznego, że poruszający się zegar zmienia swój rytm, a sztaba swą długość, podczas gdy na podstawie znajomości zjawisk mechanicznych nigdy byśmy tego nie podejrzewali. Musimy przyjąć koncepcję czasu względnego w każdym u. w., jest ona bowiem najlepszym rozwiązaniem naszych trudności. Dalszy postęp nauki, zapoczątkowany przez teorię względności, świadczy, że nie należy tego nowego poglądu uważać za zło konieczne, zbyt wyraźne są bowiem zalety tej teorii.

Staraliśmy się dotąd pokazać, co doprowadziło do podstawowych założeń teorii względności oraz jak teoria ta zmusiła nas do rewizji i zmiany transformacji klasycznej przez potraktowanie w nowy sposób przestrzeni i czasu. Celem naszym jest wskazanie idei stanowiących podstawę nowego poglądu fizycznego i filozoficznego. Idee te są proste, ale w postaci, w jakiej zostały one tu przedstawione, wystarczają tylko do wyciągnięcia wniosków jakościowych, nie prowadząc do wniosków ilościowych. Musimy się znów posłużyć naszą starą metodą wyjaśniania tylko zasadniczych pojęć i podawania niektórych innych bez dowodu.

Aby wyraźnie zdać sobie sprawę z różnicy poglądów między dawnym fizykiem, którego nazwiemy D i który wierzy w transformację klasyczną, a znającym teorię względności fizykiem współczesnym, którego nazwiemy W, wyobraźmy sobie ich dialog.

D. Wierzę w zasadę względności Galileusza w mechanice, gdyż wiem, że prawa mechaniki w dwóch poruszających się względem siebie ruchem jednostajnym układach współrzędnych są jednakowe, czyli innymi słowy, że są one niezmienne względem transformacji klasycznej.

W. Ale zasada względności musi dotyczyć wszystkich zjawisk naszego świata zewnętrznego. W u. w. poruszających się względem siebie ruchem jednostajnym powinny być jednakowe nie tylko prawa mechaniki, lecz wszystkie prawa przyrody.

D. Jakże jednak mogą być wszystkie prawa przyrody jednakowe w poruszających się względem siebie u. w.? Równania pola, to znaczy równania Maxwella, nie są niezmienne względem transformacji klasycznej. Widać to wyraźnie na przykładzie prędkości światła. Według transformacji klasycznej prędkość ta nie powinna być jednakowa w dwóch poruszających się względem siebie u. w.

W. Znaczy to po prostu, że nie można stosować transformacji klasycznej, że związek między dwoma u. w. musi być inny; że nie należy wiązać z sobą współrzędnych i prędkości tak, jak to ma miejsce w klasycznych prawach transformacyjnych. Prawa te musimy zastąpić nowymi prawami, które trzeba wyprowadzić z podstawowych założeń teorii względności. Nie będziemy się troszczyć o matematyczny kształt tego nowego prawa transformacyjnego, zadowalając się stwierdzeniem, że jest ono różne od klasycznego. Nazwiemy je krótko transformacją Lorentza . Można wykazać, że równania Maxwella, to znaczy prawa rządzące polem, są niezmienne względem transformacji Lorentza, podobnie jak prawa mechaniki są niezmienne względem transformacji klasycznej. Przypomnijmy sobie, jak to było w fizyce klasycznej. Mieliśmy prawa transformacyjne dla współrzędnych, prawa transformacyjne dla prędkości, ale prawa mechaniki były jednakowe w dwóch poruszających się względem siebie ruchem jednostajnym u. w. Mieliśmy prawa transformacyjne dla przestrzeni, ale nie dla czasu, gdyż czas był we wszystkich u. w. jednakowy. Tutaj jednak, w teorii względności, rzecz ma się inaczej. Mamy różne od klasycznych prawa transformacyjne dla przestrzeni, czasu i prędkości. Ale prawa przyrody muszą i teraz być jednakowe we wszystkich u. w., poruszających się względem siebie ruchem jednostajnym. Prawa przyrody muszą być niezmienne nie, jak przedtem, względem transformacji klasycznej, lecz względem transformacji nowego typu, tak zwanej transformacji Lorentza. Jednakowe prawa obowiązują we wszystkich inercjalnych u. w., a przejście od jednego u. w. do drugiego jest dane przez transformację Lorentza.

D. Wierzę ci na słowo, ale chciałbym znać różnicę między transformacją klasyczną a Lorentza.

W. Na twoje pytanie można najlepiej odpowiedzieć w następujący sposób. Wymień kilka charakterystycznych własności transformacji klasycznej, a ja spróbuję wyjaśnić, czy są one utrzymane w transformacji Lorentza, a jeśli nie, to jak się zmieniają.

D. Jeżeli w moim u. w. zdarzy się coś w pewnym punkcie i w pewnej chwili, to obserwator w innym u. w., poruszającym się ruchem jednostajnym względem mojego, przypisze inną liczbę położeniu, w którym zaszło zdarzenie, ale oczywiście przypisze zdarzeniu ten sam czas. We wszystkich u. w. używamy tego samego zegara i to, czy się on porusza, czy nie, nie ma żadnego znaczenia. Czy u ciebie jest tak samo?

W. Nie. Każdy u. w. musi być wyposażony w swoje własne spoczywające zegary, gdyż ruch zmienia rytm zegara. Dwaj obserwatorzy w dwóch różnych u. w. przypiszą różne liczby nie tylko położeniu, ale i czasowi, w którym zachodzi zdarzenie.

D. Znaczy to, że czas nie jest niezmiennikiem. W transformacji klasycznej mamy we wszystkich u. w. zawsze ten sam czas. W transformacji Lorentza zmienia się on, zachowując się trochę jak współrzędne w starej transformacji. Ciekaw jestem, jak jest z odległością? Według mechaniki klasycznej sztywna sztaba zachowuje swą długość zarówno w ruchu, jak w spoczynku. Czy teraz jest tak samo?

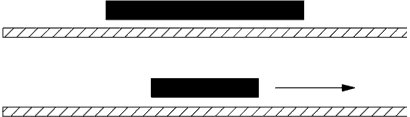
W. Nie. Z transformacji Lorentza wynika właśnie, że poruszający się pręt kurczy się w kierunku ruchu, przy czym skrócenie to wzrasta ze wzrostem szybkości. Im szybciej się pręt porusza, tym się staje krótszy. Zachodzi to jednak tylko w kierunku ruchu. Na moim rysunku widzisz poruszającą się sztabę, która kurczy się do połowy swej długości, gdy prędkość jej wynosi około 90 procent prędkości światła. Nie ma jednak skrócenia w kierunku prostopadłym do ruchu, co starałem się uwidocznić na rysunku.

D. Znaczy to, że rytm poruszającego się zegara i długość poruszającego się pręta zależą od szybkości. Ale jak?

W. Zmiany stają się wyraźniejsze w miarę wzrostu prędkości. Z transformacji Lorentza wynika, że pręt, którego szybkość osiągnęłaby wartość szybkości światła, skurczyłby się do zera. Podobnie rytm poruszającego się zegara jest zwolniony w porównaniu z zegarami mijanymi wzdłuż sztaby i zwolniłby do zera, gdyby zegar poruszał się z prędkością światła - oczywiście, jeśli to jest dobry zegar.

D. Zdaje się to przeczyć wszelkiemu naszemu doświadczeniu. Wiemy, że jadący samochód nie kurczy się i wiemy także, że kierowca może zawsze porównywać swój "dobry" zegarek z zegarami mijanymi po drodze, stwierdzając - wbrew twemu twierdzeniu - dobrą ich zgodność.

W. Masz oczywiście słuszność. Ale wszystkie te prędkości mechaniczne są bardzo małe w porównaniu z prędkością światła, toteż śmieszne jest stosowanie do tych zjawisk teorii względności. Każdy kierowca może spokojnie stosować mechanikę klasyczną, nawet jeśli zwiększy swą szybkość sto tysięcy razy. Rozbieżności między doświadczeniem a transformacją klasyczną moglibyśmy się spodziewać tylko w przypadku prędkości bliskich prędkości światła. Słuszność transformacji Lorentza można sprawdzić tylko przy użyciu bardzo wielkich prędkości.

D. Ale jest jeszcze jedna trudność. Według mechaniki mogę sobie wyobrazić ciała o prędkościach nawet większych od prędkości światła. Ciało, poruszające się z prędkością światła względem płynącego statku, ma względem brzegu prędkość większą od prędkości światła. Co się stanie z prętem, który się skurczył do zera, gdy jego prędkość była równa prędkości światła? Nie można się chyba spodziewać, że w przypadku prędkości większych od prędkości światła długość stanie się ujemna.

W. Doprawdy, nie ma powodu do takiej złośliwości! Z punktu widzenia teorii względności ciało materialne nie może mieć prędkości większej od prędkości światła. Prędkość światła stanowi górną granicę prędkości wszelkich ciał materialnych. Jeśli prędkość ciała względem statku jest równa prędkości światła, to prędkość tego ciała względem brzegu jest równa prędkości światła. Znane z mechaniki proste prawo dodawania i odejmowania prędkości już nie obowiązuje albo, dokładniej, obowiązuje tylko w przybliżeniu dla małych prędkości, ale nie dla prędkości bliskich prędkości światła. Liczba przedstawiająca prędkość światła występuje jawnie w transformacji Lorentza i odgrywa rolę przypadku granicznego, podobną do roli prędkości nieskończonej w mechanice klasycznej. Ta ogólniejsza teoria nie pozostaje w sprzeczności z transformacją klasyczną i z mechaniką klasyczną. Przeciwnie, stare pojęcia otrzymujemy z powrotem jako przypadek graniczny, gdy prędkości są małe. Z punktu widzenia nowej teorii widać wyraźnie, w jakich wypadkach obowiązuje fizyka klasyczna, jakie są granice jej zastosowań. Stosowanie teorii względności do ruchu samochodów, statków i pociągów byłoby równie śmieszne, jak stosowanie maszyny do liczenia tam, gdzie wystarcza tabliczka mnożenia.