 Czy rzeczywistość czasoprzestrzenna może być euklidesowa?
Czy rzeczywistość czasoprzestrzenna może być euklidesowa?
W tej pracy rzeczywistość czasoprzestrzenna jest opisana przy pomocy modelu euklidesowego zbudowanego z wymiarów przestrzennych obserwatora i czasu własnego obserwowanego obiektu. W wyniku otrzymujemy znaczne uproszczenie opisów wielu zjawisk i kilka wniosków różnych od przewidywanych przez Szczególną Teorię Względności
Wstęp
Opisując ruch w Szczególnej Teorii Względności korzystamy z układu współrzędnych zbudowanego z trzech wymiarów przestrzennych i czasu, który możemy zmierzyć w naszym układzie odniesienia. Przyjęcie modelu rzeczywistości zbudowanego z tych wymiarów jest z naszego punktu widzenia oczywiste - przecież są to wymiary, które możemy bezpośrednio obserwować. Odruchowo zakładamy, że "prawdziwa" rzeczywistość jest pseudoeuklidesowa, czyli taka, jaką obserwujemy.
Jednak opis zdarzeń w STW jest skomplikowany, ma też miejsce wiele zagadkowych podobieństw, których dotychczasowe teorie nie są w stanie wyjaśnić. Na przykład: podobieństwo wymiarów czasu i przestrzeni sugerujące możliwość wprowadzenia pełnej symetrii co jest jednak niemożliwe, czy też brak pełnej symetrii w równaniach Maxwella. Próby wyjaśnienia tych i innych zagadnień motywują wielu autorów do tworzenia nowych teorii, traktowanych raczej jako ciekawostki.
Skomplikowana teoria opisująca rzeczywistość może być odzwierciedleniem faktycznego stanu rzeczywistości fizycznej, lecz komplikacja taka może mieć także i inne przyczyny.
Na przykład opis ruchu planet przy założeniu, że układ odniesienia Wszechświata jest związany z Ziemią był bardzo skomplikowany. Trajektorie planet opisywały bardzo złożone, choć prawdziwe zależności. Przyjęcie takiego układu odniesienia związanego z Ziemią wydawało się logiczne. Przecież każdy od urodzenia widział, że Słońce i gwiazdy się poruszają, a Ziemia stoi w miejscu.
Dopiero powiązanie układu odniesienia ze Słońcem - niezgodne z tym co obserwowaliśmy na co dzień spowodowało uproszczenie opisu ruchu planet.
Tak więc można postawić pytanie: Czy dobrze znany, lecz skomplikowany model rzeczywistości pseudoeuklidesowej opisuje "prawdziwą" rzeczywistość fizyczną, czy też komplikacja modelu jest wynikiem opisu znacznie prostszej hipotetycznej rzeczywistości w niewłaściwym układzie współrzędnych - jak to miało miejsce przy wspomnianym opisie ruchu planet.
Ostatecznie fakt, że rzeczywistość obserwujemy jako pseudoeuklidesową nie musi oznaczać, że "prawdziwa" rzeczywistość musi być pseudoeuklidesowa. Obserwowany kształt rzeczywistości może może być na przykład efektem sposobu prowadzenia obserwacji. Przecież rzeczywistości jako takiej nie jesteśmy w stanie zaobserwować. To co obserwujemy to jedynie zdarzenia zachodzące w tej rzeczywistości i dodatkowo zdarzenia te obserwujemy też nie bezpośrednio a za pośrednictwem kwantów - cząstek rozchodzących się w sposób bardzo dziwny - z naszego punktu widzenia.
Możliwy jest jednak opis rzeczywistości przy pomocy prostszego, na przykład euklidesowego modelu. Rzeczywistość pseudoeuklidesowa jest w tym przypadku jedynie efektem obserwacji zdarzeń w tej hipotetycznej rzeczywistości.
Proponowany opis wyjaśnia m.in. wspomniany problem symetrii wymiarów czasowych i przestrzennych, oraz prowadzi do kilku wniosków odmiennych od wynikających z STW.
Konstrukcja modelu
Stan dotychczasowy:
Wymiar czasowy i wymiary przestrzenne mają tę właściwość, że przy zmianie układu odniesienia zachowywana jest wartość ds2 określona zależnością:
Przyjmuje się więc, że wymiary przestrzeni euklidesowej xyz oraz wymiar czasowy t tworzą rzeczywistość pseudoeuklidesową to jest taką, w której odległość określa właśnie wartość ds2 Przyjęcie takiej definicji rzeczywistości powoduje, że przejście od jednego układu odniesienia do drugiego poruszającego się z inną prędkością musi dawać w efekcie rozciąganie wymiarów xyz i t.
Z kolei z względności ruchu wynika fakt, że jeżeli obserwator A widzi zmianę wymiarów w układzie obserwatora B, to obserwator B widzi taką samą zmianę wymiarów w układzie obserwatora A. O tym, że jest deformacja wymiarów faktycznie ma miejsce świadczy wiele eksperymentów.
Co zatem będzie na przykład, gdy obserwator B wyruszy w podróż i wróci, a obserwator A będzie pozostawał w spoczynku? Obaj w czasie podróży będą wzajemnie obserwować spowolnienie czasu w układzie drugiego z nich, ale w którym układzie czas rzeczywiście będzie płynął wolniej? Problem ten znany jako Paradoks Bliźniąt jest interpretowany tak, że czas w układzie w podróży płynie wolniej, ponieważ zmiana kierunku lotu powoduje, że układ podróżnika przez pewien czas jest nieinercjalny. Interpretacja ta znalazła potwierdzenie wprost w eksperymencie z zegarami podróżującymi w samolotach dookoła Ziemi i chociaż do teoretycznych założeń eksperymentu można mieć zastrzeżenia, to jednak przekonanie o słuszności powyższej interpretacji jest tak silne, że eksperyment potwierdzający ten fakt został przyjęty jako oczywisty i opublikowany w najpoważniejszych czasopismach.
Jednak problemy związane z wzajemną obserwacją skrócenia Lorentza, dylatacji czasu, względnością wyboru układu odniesienia itp. są trudne do zrozumienia co powoduje, że Teorię Względności większość fizyków zna, ale mało kto naprawdę ją rozumie. Wiele problemów, jest trudnych w interpretacji co powoduje pojawianie się w literaturze rozbieżnych opinii - przytoczę tu wspomniane już wyżej prace [1,6] - sama teoria względności nie jest w stanie podać tu jednoznacznego i prostego rozwiązania.
Podobieństwo wymiarów czasu i przestrzeni pozwala zapisać równanie (1) w postaci traktującej czas i przestrzeń w jednakowy pozornie sposób:
(gdzie xi oraz xk oznaczają wymiar czasowy i,j,k=0 i trzy wymiary przestrzenne i,j,k=1,2,3).
"Pozornie" ponieważ tensor gjk jest równy a więc inaczej traktuje wymiar czasowy i wymiary przestrzenne. Taka postać tensora nie wynika już z żadnych bardziej podstawowych własności rzeczywistości i jest przyjmowana, ponieważ jest zgodna z obserwacjami. Postać ta budzi kolejne wątpliwości. Podstawową jest brak symetrii wymiarów czasu i przestrzeni. Próby wprowadzenia symetrii na przykład przez rozszerzenie liczby wymiarów czasowych do trzech, nie przyniosły pozytywnych wyników.
Przedstawiony wyżej bardzo skrótowy przekrój założeń i problemów STW pokazuje, że choć STW opisuje poprawnie większość zjawisk fizycznych to opis ten jest skomplikowany, czasami niejednoznaczny i nie potrafi wyjaśnić niektórych własności jak np. postać tensora metrycznego, którą chcąc, niechcąc przyjmujemy jako fundamentalną własność rzeczywistości. Czy zatem rzeczywistość jest tak skomplikowana, czy może jednak, jak wspomniano we wstępie, za problemy z interpretacją czy brak symetrii wymiarów odpowiada niewłaściwy układ współrzędnych?
Nowy model rzeczywistości:
Załóżmy, że wyżej wymienione własności rzeczywistości fizycznej jak na przykład jej pseudoeuklidesowy charakter nie jest własnością rzeczywistości a jedynie wynikiem sposobu prowadzenia obserwacji zdarzeń zachodzących w innej, prostszej a więc prawdopodobnie euklidesowej rzeczywistości.
Jeśli "prawdziwa" rzeczywistość byłaby euklidesowa, to pierwszym założeniem, jakie należałoby przyjąć będzie podobnie jak w STW:
Założenie 1:
Długość trajektorii ciała w nowej przestrzeni jest miarą jego czasu własnego.
UWAGA: W proponowanej rzeczywistości, dla trajektorii cząstki nie będzie używana nazwa "linia świata", ponieważ współrzędne nowej rzeczywistości będą miały określonego z góry charakteru czasowego czy przestrzennego. Analogicznie pojęcie "czasu własnego", choć będzie na razie używane, to jednak w nowym modelu rozdzielanie pojęcia "czasu" od "czasu własnego" nie będzie uzasadnione.
Jednak zasada zachowania odległości ds określonej równaniem (1) wymaga wprowadzenia jeszcze jednego założenia zapewniającego spełnianie tej zależności.
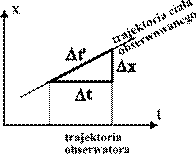
Jeśli przedstawimy trajektorie ciała obserwowanego i obserwatora w nowej, euklidesowej rzeczywistości, to wprowadzenie tradycyjnego układu xt nie powoduje zachowania tej zależności - rys 1a.
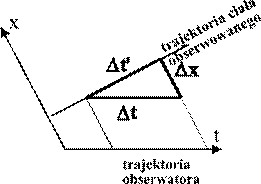
Natomiast zależność taką zachowuje wprowadzenie układu współrzędnych, w którym wymiar przestrzenny obserwatora jest prostopadły do trajektorii ciała obserwowanego - rys 1b. - pamiętamy, że w przypadku obserwacji konkretnego ciała zachodzi zależność, ds2 = dt2
 |
 |
Rys. 1a. Zastosowanie w rzeczywistości euklidesowej "tradycyjnego" układu współrzędnych, w którym oś przestrzenna obserwatora jest prostopadła do trajektorii obserwatora nie powoduje zachowania zależności (1) |
Rys. 1b. Wybór osi przestrzennej obserwatora prostopadłej do trajektorii ciała obserwowanego powoduje spełnienie zależności (1) - tu: dt'2=dt2-dx2 |
Tak więc musimy przyjąć drugie założenie:
Założenie 2:
Wymiar przestrzenny obserwatora w nowej rzeczywistości musi być prostopadły do trajektorii ciała obserwowanego.
Założenie to może wydawać się nielogiczne, ale musimy pamiętać, że wymiary tworzące nową rzeczywistość euklidesową nie są wymiarami, które możemy zaobserwować.
W praktyce oznacza to, że w nowej czterowymiarowej euklidesowej rzeczywistości wymiar obserwowany jako czasowy pokrywa się z trajektorią obserwatora, natomiast trzy kierunki interpretowane jako przestrzenne są prostopadłe do trajektorii ciała obserwowanego, a więc inne dla obserwacji każdego ciała. Tak więc jeden i ten sam kierunek raz może być interpretowany jako czasowy a raz jako przestrzenny. Wszystko zależy jedynie od wyboru obserwatora i ciała obserwowanego.
Niektóre z konsekwencji wymienionych wyżej faktów omówię w dalszej części artykułu.
Powiązanie wymiaru przestrzennego trajektorią ciała obserwowanego a nie z obserwatorem, powoduje automatyczne spełnienie warunku (1) bez konieczności pisania równań w sposób zapewniający zachowanie interwału czasoprzestrzennego, co przedstawiono na rys. 2.
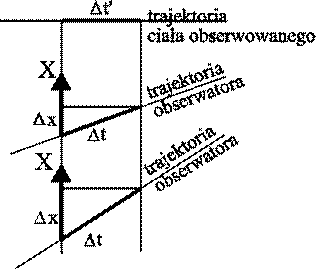 |
Rys. 2. Wybór osi przestrzennej obserwatora jako prostopadłej do trajektorii ciała obserwowanego powoduje, że równanie (1) - tu: dt'2=dt2-dx2 jest spełnione dla każdego obserwatora. Jednocześnie taki wybór osi x w naturalny sposób określa równouprawnienie wszystkich obserwatorów |
Inaczej mówiąc każde równanie napisane w nowym układzie współrzędnych automatycznie spełnia zasadę zachowania interwału czasoprzestrzennego!
Powinno to istotnie uprościć równania Ogólnej Teorii Względności, których komplikacja wynika głównie z zapisu zachowującego wartość ds2 przy zmianie układu odniesienia.
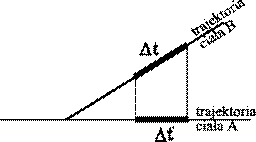
Także zagadnienie wzajemnej obserwacji np. dylatacji czasu jest tu przedstawione w sposób bardzo prosty, zrozumiały i jednoznaczny - rys.3. Widać tu, że skrócenie czasu w układzie w ruchu jest jedynie wynikiem obserwacji a nie faktyczną deformacją wymiarów.
 |
 |
Rys. 3a. Obserwatorem jest ciało B. Oś przestrzenna obserwatora jest prostopadła do trajektorii ciała A. Obserwator B widzi, że w układzie A czas płynie wolniej. |
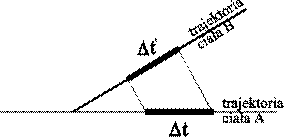
Rys. 3b. Obserwatorem jest ciało A. Oś przestrzenna obserwatora jest prostopadła do trajektorii ciała B. Obserwator A widzi, że w układzie B czas płynie wolniej |
|
W obydwu przypadkach długości odcinków Δt i Δt' są miarami czasów upływających w tych układach
Czas i przestrzeń
Kolejnym problemem jest zagadnienie interpretacji faktu, że wymiar przestrzenny nie jest stały w stosunku do obserwatora a zależy od wyboru ciała obserwowanego.
Najpierw musimy zastanowić się co decyduje o tym, że w czterowymiarowej rzeczywistości widzimy jedynie trzy wymiary przestrzenne. Problem jest nowy ponieważ w dotychczasowych teoriach mieliśmy wymiary z góry określone jako czasowe bądź przestrzenne więc nie trzeba było się zastanawiać nad sensem czasu czy przestrzeni. W tej chwili mamy cztery wymiary, z których żaden nie jest ani czasowy ani przestrzenny i dopiero proces obserwacji czyni z trzech kierunków przestrzeń a z czwartego czas.
Ponieważ przestrzeń poznajemy za pomocą oddziaływań, więc liczba wymiarów przestrzeni, które jesteśmy w stanie zaobserwować musi odpowiadać jedynie tym wymiarom, w których rozchodzą się oddziaływania niezależnie od faktycznej liczby wymiarów obiektywnej rzeczywistości. Tak więc jeśli w obiektywnej n-wymiarowej rzeczywistości oddziaływania rozchodzą się w trójwymiarowej podprzestrzeni to jesteśmy w stanie obserwować jedynie przestrzeń trójwymiarową. W dodatku musimy pamiętać, że w procesie obserwacji jesteśmy w zasadzie jedynie odbiorcą oddziaływań ponieważ nawet jeśli próbujemy oddziaływać na jakiś obiekt, to wysyłamy do niego cząsteczki, które dopiero odbite a właściwie na nowo wyemitowane przez to ciało trafiają z powrotem do nas - i dopiero one dostarczają nam informacji o otaczającej nas rzeczywistości. Tak więc fakt, że wymiary przestrzenne są prostopadłe do ciała obserwowanego można zinterpretować następująco
Założenie 3:
Cząstki przenoszące oddziaływania mogą być emitowane jedynie prostopadle do trajektorii ciała w rzeczywistości euklidesowej.
Tak więc mielibyśmy dwa podstawowe rodzaje cząstek:
Cząstki poruszające się po (istniejące na ?) trajektoriach oraz cząstki przenoszące oddziaływania - emitowane prostopadle do trajektorii tych cząstek.
Obserwowane czasy i wymiary przestrzenne dają nam w tym przypadku obraz rzeczywistości pseudoeuklidesowej, jednak nie jest to już własność rzeczywistości, która jest euklidesowa, a jedynie efekt sposobu prowadzenia obserwacji - za pomocą cząstek emitowanych prostopadle do trajektorii cząstek obserwowanych.
Jak widać taka konstrukcja rzeczywistości uzasadnia kształt tensora metrycznego w równaniu (2) a fakt, że ten sam kierunek rzeczywistości może być interpretowany jako czasowy bądź przestrzenny uzasadnia podobieństwo wymiarów czasowych i przestrzennych.
Jednocześnie zależności STW wyprowadzane są tu w sposób znacznie prostszy niż dotychczas. Na przykład transformacja Lorentza wynika natychmiast z porównania układów współrzędnych dwóch ciał w nowej, euklidesowej rzeczywistości - patrz dodatek na końcu artykułu.
Związek, między współrzędnymi euklidesowymi a współrzędnymi obserwowanymi:
W nowej euklidesowej rzeczywistości układy współrzędnych obserwatora xt i ciała obserwowanego x't' można przedstawić następująco - rys. 4:
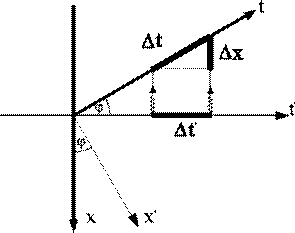 |
Rys 4. Współrzędne dwóch układów odniesienia poruszających się względem siebie z prędkością V. Miarą prędkości względnej jest sinus kąta nachylenia trajektorii obu ciał
V=Δx/Δt=sinφ
Na rysunku przedstawiono przypadek obserwacji układu x't' z układu xt . - kwanty emitowane są z układu x't' - prostopadle do osi t'.
Obserwację układu xt z punktu widzenia obserwatora x't' można przedstawić na tym samym schemacie - wystarczy przyjąć, że kwanty emitowane są z układu xt - prostopadle do osi t. Zagadnienie wzajemnej obserwacji przedstawiono na rys. 3. |
Oś przestrzenną obserwatora wybieramy tak, aby była prostopadła od trajektorii ciała obserwowanego, i podobnie oś przestrzenną układu ciała obserwowanego wybieramy tak samo - aby była prostopadła do trajektorii (osi czasu) obserwatora.
Tak więc żaden z układów xt czy x't' nie jest tu wyróżniony. To, że nazwaliśmy xt układem obserwatora jest wyłącznie umowne. Jeśli potraktujemy układ x't' jako obserwatora, to na naszym rysunku nic się nie zmieni.
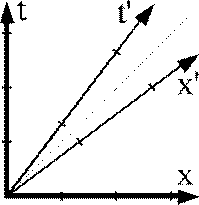
Tymczasem w STW osie współrzędnych obu układów będą wyglądały inaczej z punktu widzenia obserwatora umieszczonego w xt - rys 5a a inaczej z punktu widzenia obserwatora w x't' - rys 5b.
 |
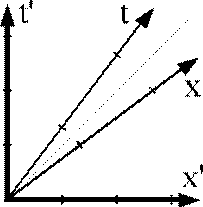 |
Rys. 5a. Obserwacja układu x't' z układu xt zgodnie z STW. Wymiary układu x't' uległy rozciągnięciu. |
Rys. 5b. Obserwacja układu xt z układu x't' zgodnie z STW. Wymiary układu xt uległy rozciągnięciu. |
Należy zauważyć, że sens prędkości względnej ma tu sinus kąta między trajektoriami obu ciał:
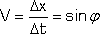 |
(3) |
przy czym prędkość jest już jedynie efektem obserwacji a nie wielkością fizyczną. Prędkość światła - tu równa 1 - odpowiada trajektorii prostopadłej do trajektorii obserwatora. Łatwo zauważyć, że stopniowe zwiększanie kąta φ do 90o będzie powodowało wydłużanie wymiaru x do nieskończoności - dla 90o wymiar x byłby równoległy do osi czasu obserwatora t. W związku z tym nawet, jeśli jest możliwa zmiana w skończonym czasie (własnym ciała przyśpieszanego) trajektorii ciała na prostopadłą do osi obserwatora, to sama obserwacja tego faktu będzie trwała w nieskończoność.
Wnioski
Założenie, że "prawdziwa" rzeczywistość jest euklidesowa, a nie pseudoeuklidesowa, jak zakładano w poprzednich modelach prowadzi do innej niż dotychczasowa interpretacji niektórych zjawisk znanych z STW.
Paradoks Bliźniąt
Na przykład opis Paradoksu bliźniąt w nowej, euklidesowej rzeczywistości musi prowadzić do wniosku, że czas bliźniaka w podróży powinien być dłuższy - czyli odwrotnie, niż jest to przewidywane w STW - rys.6. Musi tak być, ponieważ trajektoria bliźniaka w podróży jest dłuższa. Pamiętajmy, że w rzeczywistości euklidesowej trajektorie obydwu obserwatorów są tej samej skali i ich długości są równe czasom własnym.
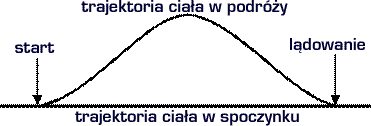 |
Rys. 6. Paradoks bliźniąt w nowej, euklidesowej rzeczywistości. |
Wniosek ten jest niezgodny z dotychczasową interpretacją paradoksu zegarów potwierdzoną przez wiele różnych eksperymentów [5]. Może to sugerować, że prezentowana teoria jest fałszywa. W rzeczywistości większość doświadczeń może być wyjaśniona zgodnie z prezentowaną teorią. Jako przykład niech posłuży interpretacja doświadczenia Pound i Rebka [3].
Autorzy pomierzyli zależność częstotliwości emitowanego promieniowania od temperatury ciała. Zmiana częstotliwości promieniowania odpowiadała relatywistycznemu skróceniu czasu jakie miało miejsce w układzie drgających atomów ciała. Szybkość drgań atomów a więc i relatywistyczne skrócenie czasu były funkcją temperatury. Wynik tego doświadczenia jest podawany w podręcznikach jako uzasadnienie obowiązującej interpretacji Paradoksu Bliźniąt, np. [8].
Zgodnie z prezentowaną tu teorią, obserwacja każdego punktu trajektorii bliźniaka w podróży lub trajektorii drgającego atomu w eksperymencie [3] daje w wyniku spowolnienie czasu identyczne jak w STW - więc pomiary jakie przeprowadzili Pound i Rebka są w zgodzie z prezentowaną teorią, która przewiduje obserwowane skrócenie czasu wg wzoru - rys.4:
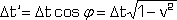 |
(4) |
gdzie j jest kątem między trajektoriami a sinφ oznacza względną prędkość ciał.
Podstawowa różnica między moją teorią a STW polega na tym, że obserwacja każdego punktu na trajektorii ciała w ruchu musi być przeprowadzona w innym układzie odniesienia, w którym oś x musi być prostopadła do trajektorii ciała obserwowanego.
Tak wiec, chociaż obserwator w każdym momencie obserwuje skrócenie czasu w układzie w ruchu to jednak łączny czas upływający w układzie w ruchu jest dłuższy niż w układzie obserwatora w spoczynku. Wyjaśnia to rys.7a.
Inaczej mówiąc nie można obliczyć czasu upływającego w układzie w ruchu jako scałkowania czasów obserwowanych w kolejnych punktach trajektorii - równanie (5).
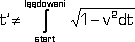 |
(5) |
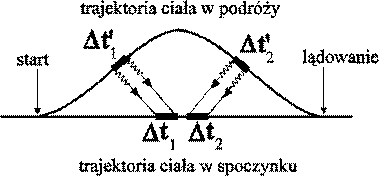 |
Fig. 7a
Obserwator w spoczynku widzi że czas w układzie w ruchu płynie wolniej: Δt'i<Δti. Jednak łączna długość czasu (trajektorii) w układzie w ruchu jest większa niż w układzie w spoczynku. Może tak być ponieważ każdy punkt trajektorii jest obserwowany w innym układzie współrzędnych, których osie x są prostopadłe do trajektorii ciała obserwowanego. |
Zgodnie z moją teorią jedynie obserwator w ruchu może obliczyć czas w układzie obserwatora w spoczynku jako całkę obserwowanych czasów - równanie (6).
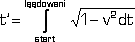 |
(6) |
Jest tak, ponieważ w tym przypadku osie przestrzenne wszystkich układów odniesienia wybieranych dla pomiaru poszczególnych punktów na trajektorii są równoległe (prostopadłe do trajektorii obserwatora w spoczynku). Obserwację z punktu widzenia obserwatora w ruchu ilustruje rys. 7b.
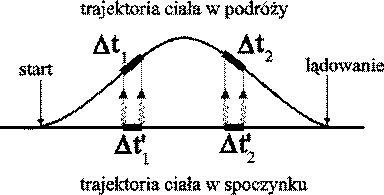 |
Fig. 7b
Obserwator w ruchu obserwuje ciało w spoczynku. Obserwator widzi, że czas w układzie w spoczynku płynie wolniej: Δt'i<Δ ti. Ponieważ osie x wszystkich układów odniesienia są równoległe, więc całkowita długość trajektorii (czasu) ciała w spoczynku jest równa sumie czasów obserwowanych w poszczególnych Δt'ipunktach trajektorii - równanie (6) |
Z powyższych rozważań wynika, że chociaż obserwacja każdego punktu trajektorii ciała w ruchu pokazuje skrócenie czasu - jak pokazali Pound i Rebka, to jednak eksperyment z zegarami w rakiecie mierzącymi czas od startu do lądowania powinien pokazać, że łączny czas w rakiecie powinien być dłuższy.
Taki eksperyment z zegarami umieszczonymi nie w rakiecie a w samolotach lecących na wschód i zachód dookoła Ziemi przeprowadzili Hafele i Keating [1] i otrzymali wyniki zgodne z dotychczasową interpretacją STW. Jest to wynik sprzeczny z przewidywaniami mojego modelu i mogę jedynie mieć nadzieję, że zagadnienie nie zostało właściwie sformułowane [6] lub zinterpretowane [9]. Na przykład zgodnie z [9] Hafele i Keating zaniedbali wpływ siły odśrodkowej powstającej w wyniku lotu samolotów na wschód i zachód. Jeśli weźmiemy tę siłę pod uwagę dostajemy efekt grawitacyjnego skrócenia czasu zależny od kierunku lotu. Powinno to zmienić oczekiwane wyniki eksperymentu o kilkaset procent.
Obserwacja oddziaływań cząstek relatywistycznych
Innym wynikiem przyjęcia założenia, że wymiar przestrzenny obserwatora jest określany przez trajektorię ciała obserwowanego jest fakt, iż ciała obserwowane jako istniejące w tym samym punkcie czasoprzestrzeni faktycznie znajdują się w innych punktach euklidesowej rzeczywistości. Tak więc cząstki obserwowane przez nas jako spotykające się w jednym punkcie mogą nie oddziaływać ze sobą - choć powinny i na odwrót - cząstki obserwowane w dwóch różnych czasach bądź położeniach - mogą oddziaływać - choć nie powinny.
Opisywane efekty powinny wzrastać z prędkością obserwowanych ciał i z odległością od nich. Opisane efekty przedstawiono na rys. 8.
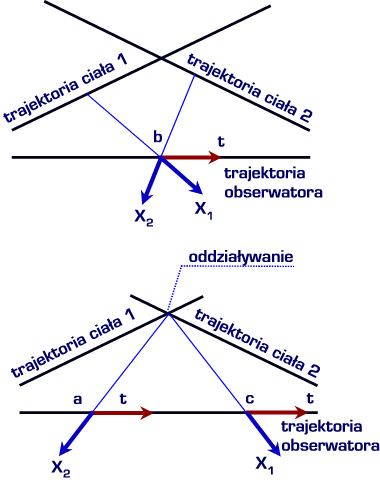 |
Rys 8. Obserwacja oddziaływania dwóch ciał w nowej rzeczywistości. Obserwacja każdego ciała wymaga wybrania innego układu współrzędnych: x2t dla obserwacji ciała 2, x1t dla obserwacji ciała 1. Punkt, w którym ciało 1 oddziaływuje jest obserwowany w czasie c, punkt w którym oddziaływuje ciało 2 w czasie a. W chwili b obserwowane odległości od obu ciał są identyczne i ciała wyglądają jakby były w tym samym punkcie czasoprzestrzeni xt |
Prędkość i szybkość światła
W prezentowanej pracy prędkość nie jest właściwością fizyczną ciał a jedynie wynikiem prowadzonej za pomocą kwantów, obserwacji trajektorii innych ciał. Właściwością fizyczną jest natomiast trajektoria w czterowymiarowej, euklidesowej rzeczywistości.
Wynikają stąd ciekawe wnioski:
Na przykład możliwe jest przyspieszenie cząstki do prędkości światła - czy obserwacja "nadświetlnych" prędkości.
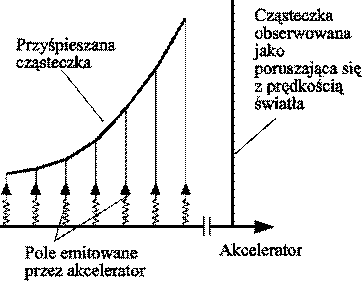
Jak już wspomniano, cząstki poruszające się po trajektorii prostopadłej do trajektorii obserwatora powinny być obserwowane jako poruszające się z prędkością światła. Ponieważ wszystkie trajektorie są dozwolone, część cząstek powinna być obserwowana jako poruszające się z tą prędkością. Innym problemem jest przyśpieszenie cząstek do tej prędkości. Łatwo wywnioskować, że przyśpieszenie cząstki w akceleratorze do prędkości światła nie jest możliwe ponieważ pole przyśpieszające w akceleratorze jest emitowane prostopadle do jego trajektorii (w wymiary obserwowane jako przestrzenne) więc przyśpieszenie cząstki do prędkości światła (do trajektorii prostopadłej do trajektorii akceleratora) wymaga nieskończonej energii i czasu - rys. 9a
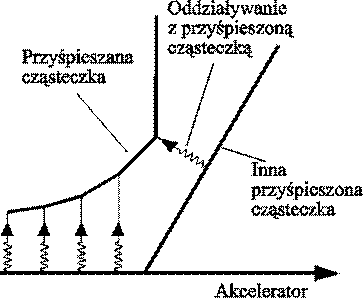
Jednak takie przyśpieszenie powinno być możliwe poprzez oddziaływanie z innymi przyśpieszonymi cząsteczkami - rys 9b. W tym przypadku powinny zostać zaobserwowane pewne niezgodności z zasadą zachowania energii. Zgodnie z moimi przybliżonymi szacunkami efekty takie powinny zacząć się pojawiać już od energii cząstek 3-5 GeV a więc znacznie poniżej maksymalnych energii uzyskiwanych obecnie w akceleratorach.
Dodatkowo, w przypadku zderzeń z innymi cząsteczkami, cząsteczka może być czasami obserwowana jako poruszająca się szybciej niż światło - rys 9c.
STW nie przewiduje możliwości osiągnięcia prędkości światła w wyniku zderzeń z innymi cząsteczkami, jednak przyjęcie założenia, że relatywistyczna zmiana wymiarów jest jedynie efektem obserwacji a nie faktyczną zmianą tych wymiarów powoduje, że reguły składania prędkości są nieco inne i umożliwiają osiągnięcie prędkości światła na przykład w przypadku zderzeń cząstek o skończonej energii. Szerzej na ten temat w następnym artykule, który obecnie jest w przygotowaniu.
|
Rys. 9a. Cząstka w akceleratorze. Przyśpieszenie cząstki do prędkości światła wymaga nieskończonego czasu i energii |
|
Rys 9b
Przyśpieszanie cząstki w wyniku zderzeń z innymi cząsteczkami. W tym przypadku jest możliwe przyśpieszenie cząstki do obserwowanej jako poruszająca się z prędkością światła. W tym przypadku można spodziewać się niezgodności z zasadą zachowania energii. |
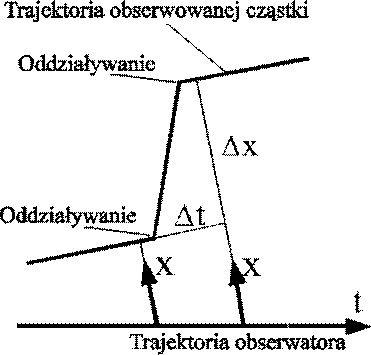 |
Fig. 9c.
Cząsteczka może być obserwowana jako poruszająca się z prędkością większą od prędkości światła. Odległość przestrzenna między dwoma punktami, w których cząstka jest obserwowana - Δx - jest większa niż odległość czasowa Δt. Obserwowany efekt jest wynikiem oddziaływania mającego miejsce między dwoma punktami, w których cząsteczka jest obserwowana. |
Nadświetlne podróże międzygwiezdne.
Zgodnie z prezentowanym tu modelem, żadna z trajektorii nie może być obserwowana jako odpowiadająca prędkości nadświetlnej czyli V>1 ponieważ prędkość definiowana jest jako sinus kąta między trajektoriami: V=sinφ. Jednak w niektórych przypadkach można określić trajektorie, wzdłuż których podróżujemy krócej, niż po trajektoriach odpowiadających szybkości światła. Jako przykład można podać podróż do bardzo szybko oddalających się układów.
Jeśli wysyłamy rakietę do układu oddalającego się od nas z prędkością bliską prędkości światła to podróż do niej z prędkością światła będzie trwała bardzo długo - rys 10. Tymczasem można określić dużo krótszą trajektorię, która umożliwi dotarcie do celu i powrót - rys 10.

Rys 10. Trajektorie światła, rakiety podróżującej z prędkością podświetlną i rakiety podróżującej krócej niż światło, ale a prędkością nie obserwowaną jako nadświetlna.
Łatwo zauważyć, że obserwacja tak podróżującej rakiety byłaby bardzo dziwna z naszego punktu widzenia. Rakieta mogłaby być prawdopodobnie obserwowana w różnych miejscach jednocześnie, jej lot mógłby być śledzony jeszcze długo po wylądowaniu a także jeszcze zanim rakieta wystartowałaby.
Podsumowanie
Przedstawiłem tu propozycję innego opisu fizycznej rzeczywistości.
Zaletą modelu jest znaczne uproszczenie opisu zdarzeń w rzeczywistości euklidesowej (jak pokazano na przykładzie Transformacji Lorentza) oraz to, że model uzasadnia jako bodajże pierwszy, sygnaturę (+ - - - ) metryki czasoprzestrzennej. Problemy względności ruchu, równouprawnienia obserwatorów, prędkości światła jako nieprzekraczalnej granicy, wzajemnej obserwacji zegarów, odległości itp. są tu opisane w sposób o wiele prostszy niż w STW i łatwy do zrozumienia. Ponadto nowy opis nie posiada osobliwości występujących w STW dla prędkości światła czy w OTW na granicy czarnych dziur (artykuł w przygotowaniu). Tak więc możliwy jest znacznie prostsze ujęcie zjawisk dotychczas trudnych do opisania w rzeczywistości pseudoeuklidesowej.
Niektóre wnioski jak na przykład interpretacja Paradoksu Bliźniąt różnią się od przewidywanych przez STW i niektórych wyników eksperymentalnych [1]. Jednak jest prawdopodobne, że doświadczenia te nie zostały poprawnie zinterpretowane [6, 9] co dawałoby szansę prezentowanej teorii.
Wiele nowych wniosków wymaga rozwinięcia - na przykład jak należy interpretować fakt, ze wymiar przestrzenny zależy od wyboru obserwowanego obiektu i jak pogodzić to w praktyce z konkretnym układem diagnostycznym mającym stałe współrzędne przestrzenne, czy jak się mają nowe reguły składania prędkości umożliwiające w praktyce osiągnięcie trajektorii obserwowanej jako ruch z prędkością światła do starych reguł, które takiego efektu nie uwzględniały. Problemy te są już rozwiązane i będą tematem następnych artykułów.
Inne wnioski, tylko zasygnalizowane - wymagają jeszcze dopracowania bądź głębszego przekonstruowania modelu. Na przykład interpretacja obserwacji ruchu rakiety podróżującej po trajektorii krótszej od świetlnej. Czy rzeczywiście jest możliwa obserwacja lotu rakiety zanim jeszcze rakieta wystartuje, czy jest to jest tylko błąd teorii? Jaki jest sens trajektorii ciała w rzeczywistości euklidesowej?
Te i inne pytania pozostają na razie bez odpowiedzi, jednak ogromna prostota modelu, wydaje się nie być kwestią przypadku i sugeruje, że przedstawione tu nowe podejście do zagadnień czasoprzestrzeni może być krokiem we właściwym kierunku.
Czy rzeczywistość czasoprzestrzenna może być euklidesowa? lub ogólniej: czy obserwowane wymiary czasu i przestrzeni są wymiarami tworzącymi "prawdziwą" rzeczywistość fizyczną czy też pewnymi projekcjami nieobserwowalnych hipotetycznych wymiarów?
W artykule przedstawiłem propozycję odpowiedzi na to pytanie, jednak problem pozostaje otwarty do dyskusji.
Dodatek: Nowy sposób wyprowadzenia równań Transformacji Lorentza w proponowanym euklidesowym układzie współrzędnych
Rozpatrzmy proste zagadnienie dwóch inercjalnych ciał w nowej rzeczywistości euklidesowej opisanej w pracy. Wyprowadzenie transformacji Lorentza przedstawiono poniżej.
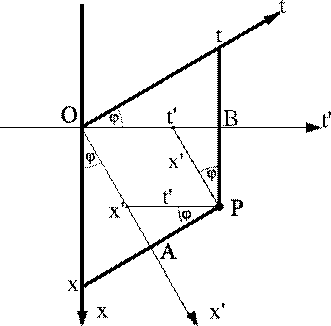 W układzie współrzędnych jak na rys. 4 umieścimy punkt P - rys.11. Z rysunku wynika, że współrzędna x punktu P jest równa: W układzie współrzędnych jak na rys. 4 umieścimy punkt P - rys.11. Z rysunku wynika, że współrzędna x punktu P jest równa:
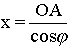
dalej:
OA=x'+ t'sinφ
tak więc, jeśli pamiętamy, że sinj oznacza prędkość ciała V (rys.4) możemy zapisać:

W ten sam sposób otrzymujemy równanie dla współrzędnej t:

OB=t'+ x'sinφ
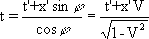
References:
1. J.C.Hafele, R.E.Keating, Science 177 p. 166-170 (1972)
2. W.Nawrot and oth. Annual Report 1986, Institute For Nuclear Studies Otwock-Swierk Poland, Department for Thermonuclear Research, Raport IPJ 2040/P-V/A 1986
3. R.V.Pound, G.A. Rebka, Physical Review Letters, 4 No 6 274-275 (1960)
4. E.Recami, Revista Nuovo Cimento, 4 No 2 209-290 (1974)
5. S.Scleif (1998)
6. R.Shlegel, Nature Phys. Sci. 229 p.237-238 (1971)
7. Nature, 223 p.519 (1971)
8. Po polsku: E.T. Taylor, J.A. Wheeler, Fizyka Czasoprzestrzeni, PWN Warszawa 1972 str. 236
Tytuł oryginału: E.T. Taylor, J.A. Wheeler, Spacetime Physics H.Freeman and Company, San Francisco and London 1966.
10. J.Strand, J. Phys. A: Math. Gen. vol.13, (1980), pp. L389-L391
11. P.T.Pappas, Lett. Nuovo Cim. vol. 25, n. 14 (1979) pp.429-433
12. R.Mignani, E.Recami, Lett. Nuovo Cim. vol. 16 n.15, (1976) pp. 449-452
13. E.A.B.Cole, Phys.Lett. vol.76A, no 5,6 (1980) pp.371-372
14. G.Dattoli, R.Mignani, Lett. Al. Nuovo Cim. vol.22 n.2 (1978), pp.65-68 |