Zadanie

Zadanie. Ruch jednostajny.

Między wyspami znajdującymi się na rzece jest odległość l=1200m. Prędkość prądu rzeki wynosi 1,8 km/h względem brzegu rzeki.
Prędkość statku względem wody jest równa 10,8 km/h.

Obliczyć, o ile będzie dłuższy czas płynięcia pod prąd rzeki niż czas płynięcia z prądem rzeki.

Rozwiązanie

Dane

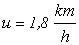
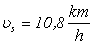
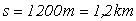
Szukane

Rozwiązanie

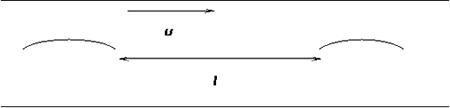
Zakładamy, że:
- rzeka jest prosta a woda płynie tak samo w każdym miejscu;
- silnik łódki pracuje stale z taką samą mocą;
- prędkość statku względem wody jest stała;
- pomijamy czas rozpędzania i hamowania statku.

To zadanie ma wiele możliwych sposobów rozwiązania. My doprowadzimy, poprzez przekształcenia, do otrzymania jednego wzoru na różnicę czasów przeprawy przez rzekę.

Oznaczamy, że prędkość płynięcia "z prądem" rzeki wyraża się wzorem:
,

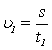Oznaczamy, że prędkość płynięcia "pod prąd" rzeki wyraża się wzorem:
.

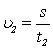Po przekształceniu tych wzorów otrzymamy wzory na obliczenie czasu płynięcia między wyspami.

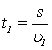
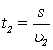
Bez względu na to, w którą stronę płyniemy, odległość między wyspami jest stała. Prędkości z jakimi będzie się poruszał statek będą różne w przypadku płynięcia "z prądem" i "pod prąd". Przecież statek znajduje się w ruchomym ośrodku. Prędkość wypadkowa statku będzie, w jednym przypadku, różnicą a w drugim sumą prędkości własnej statku i prędkości płynięcia rzeki. [tu można podać bardzo podobny przykład ruchomych schodów - można, idąc w odwrotną stronę niż kierunek ruchu schodów, znaleźć taką prędkość naszego schodzenia, że względem otoczenia będziemy znajdowali się w spoczynku]

Więc:



Podstawiając wartości tych prędkości do wzorów na czasy płynięcia otrzymujemy:

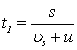
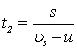
Jak widać, te wyrażenia pokazują jak obliczamy czasy płynięcia statkiem z uwzględnieniem prędkości rzeki. Szukamy różnicy tych czasów, więc:

Rozwijając to wyrażenie poprzez podstawienie odpowiednich wzorów mamy:

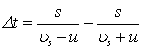
Przekształcając dalej:



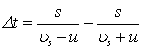
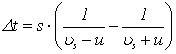
sprowadzamy do wspólnego mianownika

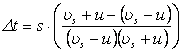
Po wymnożeniu w mianowniku i zsumowaniu w liczniku otrzymujemy:

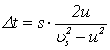
Tak wyraża się poszukiwana różnica podróży po rzece.

Obliczenia:

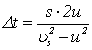
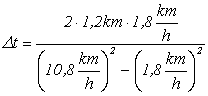
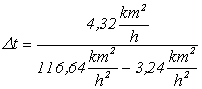
wielkość km² ulegnie skróceniu


zamieniając to na minuty


oraz na sekundy

 

Odpowiedź

Statek płynący z nurtem rzeki przebędzie odległość między wyspami w czasie o 2,28 min szybciej niż w przypadku gdy będzie płynął przeciwnie do nurtu rzeki.

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Prędkość, jak szybko porusza się ciało

Kinematyka

Kinematyka - wzory

Linki

...

Zadania z przedmiotu

Zadania