2007-03-20 Ostatnia modyfikacja.
Zadanie
Zadanie. 
Ruch ładunków w polu magnetycznym.
Omów ruch naładowanej cząstki ładunków polu magnetycznym.
Rozwiązanie
Rozwiązanie
Ruch ładunków w polu magnetycznym
Na poruszający się ładunek w polu magnetycznym o indukcji B, działa siła zmieniająca kierunek prędkości tego ładunku.
Rozpatrzymy ruch ładunku w jednorodnym polu magnetycznym. Rodzaj ruchu i kształt toru zależeć będą od prędkości początkowej, jaką nadaje się ładunkowi. Ze względu na tę prędkość początkową rozróżnimy kilka przypadków ruchu.
Przypadek I
W pole magnetyczne o indukcji B wpada ładunek q z prędkością początkową v w taki sposób, że wektory v i B są równoległe.
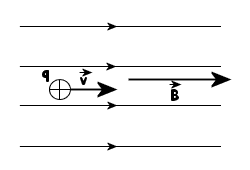
Na poruszający się w polu magnetycznym ładunek działa
siła Lorentza 
, gdzie a jest kątem między kierunkiem wektora v a kierunkiem wektora B. Ponieważ
jednak a =
0, więc sina = 0 a z tego wynika, że wartość siły wyliczona ze wzoru jest równa
zeru. Jeżeli więc na poruszający się ładunek nie działa żadna siła to
zgodnie z I zasadą dynamiki, ładunek w tym przypadku poruszać się
będzie ruchem jednostajnym prostoliniowym, zachowując nadaną mu prędkość
równoległą do linii pola.
Przypadek II
W pole magnetyczne o indukcji B wpada ładunek q z prędkością początkową v w taki sposób, że wektory v i B są prostopadłe.
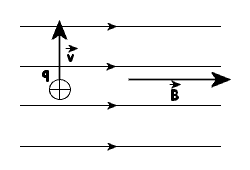
Na poruszający się w polu magnetycznym ładunek działa
siła Lorentza .
a
= 90, więc sina = 1 a z tego wynika, że wartość siły wyliczona ze wzoru jest w tym
przypadku maksymalna i równa jest co do wartości 
. Zwrot siły wyznaczony za pomocą
reguły Fleminga jest skierowany jak na rysunku. Ważne jest by pamiętać
o tym, że wektor siły w każdej chwili jest prostopadły do wektora B i
V. Oznacza to, że na rysunku przedstawiamy kierunek siły w pierwszym momencie
rozpatrywanego ruchu. Linie indukcji skierowane są prostopadle do kartki
(wychodzą ze strony).
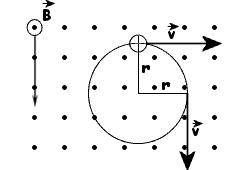
Siła Lorentza jest w każdym punkcie toru prostopadła do wektora prędkości.
Taka siła nie powoduje zmiany wartości prędkości, lecz zakrzywia tor ruchu.
Jest więc siłą dośrodkową. Fakt, że siła Lorentza jest siłą dośrodkową
wyrazimy równością:
stąd:
Ładunek w tym przypadku porusza się ruchem jednostajnym po okręgu o wyżej podanym promieniu, a okresie obliczonym ze wzoru na prędkość liniową :
stąd okres :
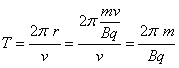
i częstotliwość :
Przypadek III
Ładunkowi q nadaje się prędkość początkową skierowaną pod kątem 0 < α < 90° do linii pola magnetycznego.
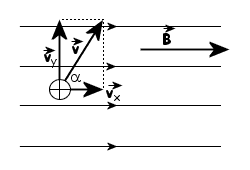
Prędkość początkową rozkładamy na składowe: równoległą
do linii pola vx i prostopadłą do linii pola vy.
Gdyby ładunek posiadał jedynie prędkość vx , poruszałby
się jak w przypadku I ruchem jednostajnym prostoliniowym, równolegle do
linii pola. Gdyby zaś ładunek miał jedynie prędkość prostopadłą do linii
pola vy , poruszałby się jak w przypadku II tj. ruchem
jednostajnym po okręgu. Ponieważ ładunek posiada obie prędkości składowe,
więc wykonuje oba wyżej wymienione ruchy składowe jednocześnie.
Torem ruchu wypadkowego jest linia śrubowa.
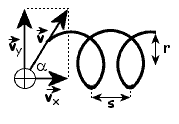
Promień śruby r obliczamy jak w przypadku II:
Okres jednego obiegu T obliczamy również jak w przypadku II:
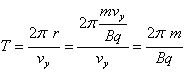
Skok linii śrubowej s jest równy drodze przebytej przez ładunek ruchem jednostajnym z prędkością vx, wzdłuż linii pola, w czasie okresu T.
Odpowiedź
Dyskusja
Zadania z przedmiotu
Zadania