 Elektrostatyka Elektrostatyka
Ładunek elektryczny - prawo Coulomba
Wszystkie ciała zbudowane są z ogromnej liczby
atomów. Atomy zaś zbudowane są z jądra atomowego,
oraz krążących wokół niego elektronów. Zarówno
jądro, jak i elektrony obdarzone są ładunkiem
elektrycznym. Jądro jest dodatnie, a elektrony
są ujemne. Oznaczamy te ładunki znakami "+" i "-". Oznaczenie który ładunek jest dodatni,
a który ujemny było i jest całkowicie umowne i
nie miało by to znaczenia, gdyby naukowcy zrobili
to na odwrót. Ładunek pojedynczego elektronu zwany jest ładunkiem elementarnym, oznaczamy
go symbolem: -e (minus, ponieważ ładunek
elektronu jest ujemny), a ma on wartość:
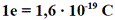
C oznacza jednostkę, którą nazywamy kulombem.
Jest ona podstawową jednostką układu SI. Taki
sam ładunek tylko, że dodatni ma jądro atomu wodoru.
Natomiast atomu helu ma ładunek 2e. Ładunek atomu
jest uzależniony od liczby atomowej danego pierwiastka.
Każde jądro atomowe składa się z protonów, których
jest dokładnie tyle ile wynosi liczba atomowa
(porządkowa) danego pierwiastka, oraz pewnej liczby
neutronów. Tylko protony w atomie są obdarzone
ładunkiem, a wartość tego ładunku wynosi +e.
Neutrony w jądrze atomowym nie są obdarzone ładunkiem.
W jądrze wodoru występuje tylko jeden proton i
to właśnie dlatego jego jądro ma ładunek równy
e.
Padło już sformułowanie, że ładunek elektronu
jest ładunkiem elementarnym. Jest on tak nazwany,
ponieważ każdy spotykany ładunek w przyrodzie
jest całkowitą wielokrotnością ładunku elementarnego.
Nie występują cząsteczki, które mają ładunek np.
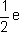
Jeszcze innym powodem, dla którego powstało określenie
ładunku elementarnego jest sposób w jakim elektryzują
się ciała. Jeżeli w jakimś ciele znajduje się
tyle samo elektronów co protonów, to mówimy, że
ciało to nie jest naelektryzowane. Jeżeli występuje
w nim więcej elektronów niż protonów to mówimy,
że ciało to jest naelektryzowane ujemnie. W przeciwnym
przypadku - więcej protonów niż elektronów - ciało
jest naelektryzowane dodatnio. Dlatego jeżeli
jakiekolwiek ciało jest naelektryzowane (czy to
dodatnio czy ujemnie), to jego ładunek jest zawsze całkowitą wielokrotnością ładunku elementarnego.
.gif)
Jak wiemy z doświadczeń, naelektryzowane ciała
oddziałują na siebie. Jeżeli naładujemy dwie kulki
ładunkami odpowiednio q1 i q2,
to zaobserwujemy, że działają one na siebie pewną
siłą. Siłę tą scharakteryzował francuski fizyk
Karol August Coulomba w 1785r:
Dwa
ładunki punktowe działają na
siebie siłą, która jest wprost
proporcjonalna do iloczynu wartości
tych ładunków, a odwrotnie proporcjonalna
do kwadratu odległości między
nimi.
Siłę tą nazywamy siłą Coulomba. Zależy
ona jeszcze od otoczenia, w jakim znajdują się
te ładunki.
Prawo to można przedstawić za pomocą wzoru:
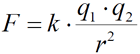
w którym:
F - siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych,
q1 , q2 - punktowe ładunki elektryczne,
r - odległość między ładunkami,
k - współczynnik proporcjonalności:
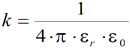
gdzie:
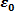 - przenikalność elektryczna próżni - przenikalność elektryczna próżni
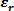 - względna przenikalność elektryczna ośrodka - względna przenikalność elektryczna ośrodka
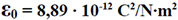
Właśnie współczynnik proporcjonalności "k" zależy od otoczenia. Dla próżni
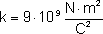
By uogólnić wzór stosuje się inne oznaczenie
współczynnika proporcjonalności:
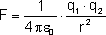
gdzie 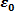 to przenikalność dielektryczna próżni to przenikalność dielektryczna próżni
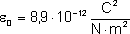
I tak wygląda wzór na siłę, z jaką oddziałują
na siebie dwa ładunki punktowe umieszczone w
próżni w odległości r.
Jeżeli ładunki te umieszczone są w innym środowisku
niż próżnia to stosuje się nieco inny współczynnik
proporcjonalności:
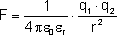
gdzie 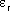 to względna przenikalność dielektryczna danego
środowiska. Dla próżni wynosi ona 1. W zależności
od środowiska przyjmuje ona inne wartości, a jakie
to można dowiedzieć się z odpowiednich tabel.
Warto też wiedzieć, że w powietrzu przenikalność
dielektryczna jest prawie taka sama jak w próżni,
więc prawie zawsze stosuje się wzór dla próżni. to względna przenikalność dielektryczna danego
środowiska. Dla próżni wynosi ona 1. W zależności
od środowiska przyjmuje ona inne wartości, a jakie
to można dowiedzieć się z odpowiednich tabel.
Warto też wiedzieć, że w powietrzu przenikalność
dielektryczna jest prawie taka sama jak w próżni,
więc prawie zawsze stosuje się wzór dla próżni.
Łatwo zauważyć, że prawo Coulomba jest bardzo
podobne do prawa powszechnego ciążenia Newtona.
Występuje jednak zasadnicza różnica. Siły grawitacji
były zawsze siłami przyciągania. Siły Coulomba
mogą zarówno przyciągać dwa ciała jak i je odpychać
od siebie. Zależy to od ładunku tych ciał. Jeżeli
ładunki tych ciał są różnoimienne (jeden ładunek
jest dodatni, a drugi ujemny) to ciała te będą
się wzajemnie przyciągać. W przeciwnym wypadku
(oba ładunki są dodatnie, albo oba są ujemne)
ciała te będą się wzajemnie odpychać.
Kierunek działania siły oddziaływania ładunków wyznaczony jest przez
prostą łączącą oba te ładunki, natomiast o zwrocie decydują znaki
ładunków. Jeżeli są one jednoimienne, oddziaływanie jest odpychaniem. W
przypadku ładunków różnoimiennych ładunki przyciągają się.
Aby uświadomić sobie jak mocne jest to oddziaływanie
w porównaniu do oddziaływania grawitacyjnego wyliczmy,
z jaką siłą oddziałują na siebie dwa ładunki punktowe
oddalone od siebie o 1 metr, naładowane oba ładunkiem
1C:
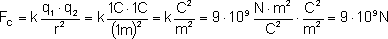
W dziale grawitacja wyliczyliśmy, z jaką siłą
oddziałują na siebie dwa ciała o masie 1 kg, oddalone
od siebie o 1 m:
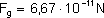
Różnica jest spora.
Elektryzowanie ciał
Elektryzowanie ciał to proces przekazywania im
ładunku. Polega on oczywiście na dodaniu, lub
odebraniu elektronów z tego ciała. Wyróżniamy
trzy sposoby elektryzowania: przez potarcie, dotyk
i indukcję.
Elektryzowanie przez potarcie
Na pewno znacie takie zjawisko, które możemy bardzo
często zaobserwować po wymyciu i wysuszeniu włosów,
kiedy próbujemy je rozczesać. Bardzo często takie
włosy przyciągają się z grzebieniem. Otóż podczas
czesania włosów następuje proces elektryzowania
ich. Włosy takie "stają dęba", ponieważ naładowane
są jednoimiennymi ładunkami (wszystkie włosy są
naelektryzowane tak samo - nie ma możliwości,
by jeden włos naelektryzował się dodatnio, a drugi
ujemnie). Ładunkiem o przeciwnym znaku ładuje
się grzebień. By sprawdzić, że grzebień też jest
naelektryzowany można wykonać proste doświadczenie.
W tym celu należy taki grzebień zbliżyć do małego
strumyka wody lecącej z kranu. Strumyk ten powinien
się odchylić od pionu. Odchylenie to będzie tym
większe im bardziej naelektryzowany był grzebień.
Elektryzowanie przez potarcie polega na tym, że
podczas pocierania dwóch ciał, jedno z nich "gubi"
elektrony, a drugie je przyłącza. W ten sposób
to pierwsze ciało ładuje się ładunkiem dodatnim,
a drugie ujemnym. Tylko jak sprawdzić które ciało
naelektryzowało się dodatnio, a które ujemnie.
Problem nie jest taki prosty, ale możemy wykorzystać
doświadczenia innych. Otóż wiadomo, że jeżeli
laskę ebonitową pocieramy wełną to laska ta naładuje
się ładunkiem ujemnym a wełna dodatnim. Natomiast
jeżeli laskę szklaną pocieramy jedwabiem, to szkło
naelektryzuje się dodatnio, a jedwab ujemnie.
Wiedząc to łato już możemy ocenić czy ładunek
na jakimś ciele jest dodatni, czy ujemny.
.gif)
Elektryzowanie przez dotyk
Aby użyć tej metody, musimy już mieć jakieś naelektryzowane
ciało. Często stosuje się do tego naelektryzowaną
ujemnie laskę ebonitową. Jeżeli więc mamy taka
laskę i obojętną kulkę metalową (odizolowaną od
otoczenia), to możemy stwierdzić, że na jednym
ciele jest nadmiar elektronów (laska ebonitowa),
a na drugim występuje równowaga (ciało jest obojętne).
W przyrodzie możemy zaobserwować zjawisko wyrównywania
się stanów, tzn. po zetknięciu się danych dwóch
ciał ładunki na nich zmienią się tak by na obu
były równe. Elektrony z laski ebonitowej przepłyną
na metalową kulkę. Laska ebonitowa nadal będzie
naładowana ujemnie, ale już ładunek ten będzie
mniejszy. Natomiast obojętna dotychczas kulka
zostanie naelektryzowana i ładunek laski i kulki
będzie taki sam.
Elektryzowanie przez indukcję
By zaobserwować jak działa ten rodzaj elektryzowania
potrzebny nam będzie elektroskop i naładowana
ujemnie laska ebonitowa. Niech elektroskop będzie
elektrycznie obojętny. Naelektryzowaną laskę zbliżmy
do elektroskopu, ale go nie dotykajmy. Zauważymy,
że listki elektroskopu wychylą się. Wiemy, że
ładunki ujemne się odpychają. Ujemnie naelektryzowana
laska ebonitowa odpycha elektrony z elektroskopu
i uciekają one do jego wnętrza na jego listki.
We wnętrzu elektroskopu występuje nadmiar elektronów
a na zewnątrz ich niedobór (tam, do którego miejsca
zbliżyliśmy laskę). Jeżeli laskę oddalimy od elektroskopu,
nadmiar elektronów z wnętrza elektroskopu zostanie
zniwelowany, bo elektrony wrócą z powrotem na
swoje poprzednie miejsce.
.gif)
Zbliżmy jeszcze raz laskę do elektroskopu, tak
by jego listki się odchyliły. Ale tym razem dotknijmy
palcem (nie laską) elektroskopu. Nasz palec będzie
działał jak uziemienie. Elektrony odepchnięte
na listki będą "szukały" dalszej drogi by jak
najdalej uciec od ujemnej laski i przez nasz palec
opuszczą elektroskop. Listki z powrotem opadną.
Zabierzmy teraz palec z elektroskopu - sytuacja
nie zmienia się. Ale zabierzmy teraz naelektryzowaną
laskę, którą cały czas trzymaliśmy blisko elektroskopu,
wówczas listki ponownie się odchylą. Dzieje się
tak dlatego, że elektrony uciekły przez nasz palec
bo były odpychane, przez laskę. Ale jak zabraliśmy
palec i laskę, to okazało się, że w elektroskopie
jest niedobór elektronów, bo miały odciętą drogę
powrotu (najpierw zabraliśmy palec, a dopiero
później laskę).
.gif)
Rozkład ładunku na powierzchni
przewodnika
Do tej pory mówiliśmy przeważnie o ładunku punktowym.
Ale sytuacja taka, że źródłem pola jest ładunek
skupiony w jednym punkcie jest w zasadzie niemożliwa.
Najczęściej do czynienia mamy z ładunkami rozmieszczonymi
na przewodniku liniowym czy powierzchni. Dlatego
też stosuje się pojęcie liniowej gęstości ładunku
lub powierzchniowej gęstości ładunku:
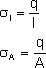
gdzie l to długość przewodnika - liniowa
gęstość ładunku, natomiast A to powierzchnia
na której rozmieszczony jest ładunek w przypadku
powierzchniowej gęstości ładunku.
Do badania rozkładu ładunku na powierzchni służy
nam elektroskop i metalowa kulka umieszczona na
izolowanym uchwycie. Dzięki tej kulce możemy zbierać
ładunek z badanej powierzchni.
Naelektryzujmy konduktor kulisty. Za pomocą kulki
zbierzmy ładunek z wnętrza konduktora i przenieśmy
go na elektroskop. Wynik jest zaskakujący, bo
listki konduktora nie wychylają się.
Oznacza to,
że ładunek nie gromadzi się we wnętrzu konduktora.
Powtórzmy doświadczenie, ale tym razem dotknijmy
kulką zewnętrzną część konduktora i przenieśmy
ładunek na elektroskop. Tym razem zgodnie z oczekiwaniami
listki elektroskopu wychylają się.
.gif)
Wykonajmy kolejne doświadczenie. Naelektryzujmy
takim samym ładunkiem dwie kule. Niech większa
kula ma promień równy R, a mniejsza promień r. Teraz dotknijmy naszą izolowana kulką
jedną z naelektryzowanych kul i przenieśmy ładunek
na elektroskop. Następnie rozładujmy elektroskop.
I powtórzmy doświadczenie przenosząc ładunek z
drugiej kuli. Porównując wychylenia listków elektroskopu
stwierdzimy, że bardziej wychyliły się po przeniesieniu
ładunku z mniejszej kuli.
.gif)
Możemy wysnuć następujący wniosek: na bardziej
zakrzywionej powierzchni gęstość powierzchniowa
ładunku jest większa.
Pojemność elektryczna
Doświadczenia pokazują, że takie wielkości jak
dostarczony ładunek na przewodnik i potencjał
tego przewodnika są wielkościami proporcjonalnymi.
Oznacza to, że stosunek:
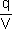
jest dla przewodnika wielkością charakterystyczną.
Oznaczono tę wielkość jako pojemność elektryczna
danego przewodnika. Wielkość tę oznaczamy symbolem C, a jednostką pojemności jest Farad.
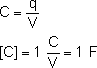
Jeden farad to pojemność takiego przewodnika,
którego potencjał wynosi 1 wolt po naładowaniu
go ładunkiem 1 kulomba.
Ze wzoru mogłoby wynikać, że pojemność przewodnika
zależy od przyłożonego ładunku lub od potencjału
tego ładunku. Jednak jak było to wspomniane te
wielkości są proporcjonalne i pojemność na zależy
od innego czynnika. Tym czynnikiem jest wielkość
przewodnika. Łatwo to sobie wyobrazić, bo większe
przewodniki mają większa pojemność elektryczną.
Kondensatory - energia kondensatorów
Jednak pojęcie pojemności przewodnika nie jest
wykorzystywane w przypadku pojedynczych przewodników,
ale raczej w ich układach. Takim układem przewodników
jest kondensator. Tworzą go dwa przewodniki
o różnych kształtach i wymiarach. Bardzo często
przewodniki te nazywamy okładkami kondensatora.
Przewodniki te ładują się takim samym ładunkiem,
ale o różnych znakach. Bardzo ważną wielkością
w kondensatorze jest różnica potencjałów tych
przewodników. Jak już było wspomniane wcześniej,
taką różnicę potencjałów nazywamy napięciem. Różnica
potencjałów jest tym większa im większy ładunek
naniesiemy na jeden z przewodników. Stosunek tego
ładunku do napięcia kondensatora jest stały i
nazywa się go pojemnością kondensatora.
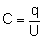
Także w tym przypadku jednostką pojemności jest farad.
Naładowany kondensator ma energię potencjalną.
Aby obliczyć jej wartość musimy wyznaczyć pracę
potrzebną do naładowania kondensatora. Skorzystajmy
ze wzoru:
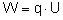
Jednak podczas ładowania kondensatora napięcie
na okładkach zmienia się. Więc chcąc użyć ten
wzór musimy zastosować średnie napięcie. Skorzystamy
z następujących faktów. Wiemy, że przed naładowaniem
kondensatora napięcie na jego okładkach równe
jest zero, a po naładowaniu wynosi U. Drugim
faktem jest to, że napięcie zmienia się z powodu
dostarczanego ładunku. Ale wiemy, że napięcie
i ładunek są wielkościami proporcjonalnymi (wykresem
zależności napięcia od ładunku jest linia prosta).
Dlatego szukając średniego napięcia przy ładowaniu
kondensatora, możemy skorzystać ze średniej arytmetycznej:
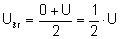
Podstawiając do wzoru na pracę:
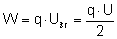
Tyle wynosi praca, jaką należy wykonać by naładować
kondensator, więc tyle też wynosi energia potencjalna
naładowanego kondensatora.
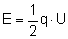
Łączenie kondensatorów
Kondensatory możemy łączyć w baterie. Oznacza
to budowanie układów kondensatorów, który to układ
(ta bateria) ma swoją pojemność. Omówimy tu dwa
sposoby łączenia: szeregowe i równoległe oraz
sprawdzimy ile w tych przypadkach wynosi pojemność
układu. Taką pojemność nazywamy pojemnością zastępczą.
Mówiąc inaczej jest to pojemność takiego kondensatora,
którym moglibyśmy zastąpić ten układ i nie wywołać
przy tym zmiany pojemności.
I jeszcze jedna uwaga, na schematach kondensator
przedstawiamy tak:
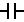
Łączenie szeregowe
Połączmy trzy kondensatory w sposób szeregowy.
Niech ich pojemności wynoszą odpowiednio C1, C2 i C3. Jeden
koniec układu naelektryzujmy dodatnio a do drugiego
podepnijmy uziemienie. Pierwsza blaszka na pierwszym
kondensatorze naładowana jest przez nas dodatnio
ładunkiem +Q. Pod wpływem indukcji druga
blaszka tego kondensatora elektryzuje się ujemnie
ładunkiem ujemnym ale o takiej samej wartości: -Q. Ale kiedy elektryzuje się ujemnie pobiera
elektrony z pierwszej blaszki drugiego kondensatora,
który w konsekwencji naładowany jest dodatnio
ładunkiem +Q. Druga okładka drugiego kondensatora
ładuje się przez indukcję ładunkiem -Q.
Następne kondensatory ładują się analogicznie
jak poprzednie. Zawsze jednak na blaszkach powstają
ładunki +Q lub -Q. Więc przyjmujemy,
że ładunek dostarczony do każdego kondensatora
wynosi Q.
.gif)
Wyliczmy ile wynosi pojemność każdego kondensatora:
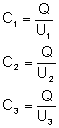
Spójrzmy teraz na wykres zależności potencjału
od długości przewodnika. Na jednym końcu wynosi
on V (ten koniec, na który naniesiony był
ładunek). Drugi koniec układu jest uziemiony,
a wszystko co jest uziemione ma potencjał równy
zero. Widzimy, że spadki potencjału mają miejsce
na kondensatorach i spadki te są równe napięciu,
jakie występuje na okładkach kondensatora. Na
wykresie widać że napięcie całego układu (różnica
potencjałów przewodnika przed pierwszym kondensatorem
i przewodnika uziemionego) jest równa sumie napięć
wszystkich kondensatorów. Wyliczmy zatem te napięcia
na każdym kondensatorze i wyliczmy ich sumę:
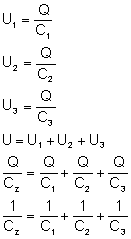
CZ to pojemność zastępcza całego
układu (pojemność baterii kondensatorów). Takim
wzorem obliczamy pojemność układów kondensatorów
połączonych szeregowo.
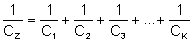
Warto wiedzieć, że pojemność zastępcza układu
połączonego szeregowo jest zawsze mniejsza od
najmniejszej pojemności łączonych kondensatorów
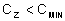
Łączenie równoległe
Połączmy teraz trzy kondensatory w sposób równoległy.
Niech każdy z nich ma pojemność równą odpowiednio C1, C2 i C3.
Tak jak poprzednio niech jeden koniec układu zostanie
naładowany dodatnio, a drugi niech będzie uziemiony.
Mamy do czynienia z następującą sytuacją: na kondensatorze
pierwszym znajduje się ładunek Q1, na kondensatorze
drugim - ładunek Q2, a na trzecim - Q3.
Ale na wszystkich kondensatorach mam identyczne
napięcie, bo wszystkie lewe (dostosuj rysunek
do opisu - okładki po lewej stronie mają być naładowane
dodatnio) okładki są połączone przewodnikiem,
więc mają wszystkie równy potencjał V.
Natomiast prawe okładki są uziemione, więc ich
potencjał równy jest zero.
.gif)
Ładunek naniesiony na lewą stronę układu rozmieścił
się po okładkach. Suma ładunków na poszczególnych
kondensatorach równa jest ładunkowi dostarczonemu
przez nas (ładunek całkowity).
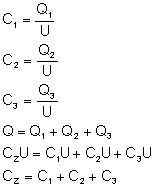
Ostatni wzór mówi nam jak liczy się pojemność
układu kondensatorów połączonych równolegle. Pojemność
zastępcza tak połączonych kondensatorów jest równa
sumie poszczególnych pojemności.
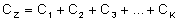
|