::: Iwiedza ::: - Ty tu rządzisz!

Równania Maxwella

Cztery fundamentalne równania elektromagnetyzmu sformułowane przez Jamesa Clerka Maxwella. Opisują one własności pola elektrycznego i magnetycznego oraz zależności między tymi polami. Z równań Maxwella można wyprowadzić równanie falowe fali elektromagnetycznej propagującej się (rozchodzącej się) w próżni z prędkością światła:
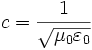$c = {1 \over \sqrt{\varepsilon_0 \mu_0}}$ .

Równania Maxwella

Lp.	Postać różniczkowa	Postać całkowa	Nazwa	Fizyczne fakty wynikające z równań
1.	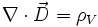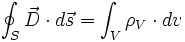$\nabla \cdot \vec{D} = \rho_V$	$\oint_S \vec{D} \cdot d\vec{s} = \int_V \rho_V \cdot dv$	prawo Gaussa dla elektryczności	Źródłem pola elektrycznego są ładunki
2.	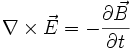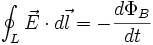$\nabla \times \vec{E} = -\frac{\partial \vec{B}} {\partial t}$	$\oint_L \vec{E} \cdot d\vec{l} = -\frac{d\Phi_B}{dt}$	prawo Faradaya	Zmienne w czasie pole magnetyczne wytwarza wirowe pole elektryczne
3.	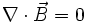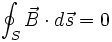$\nabla \cdot \vec{B} = 0$	$\oint_S \vec{B} \cdot d\vec{s} = 0$	prawo Gaussa dla magnetyzmu	Pole magnetyczne jest bezźródłowe,linie sił pola magnetycznego są zamknięte
4.	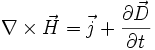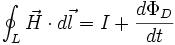$\nabla \times \vec{H} = \vec{j} + \frac{\partial \vec{D}} {\partial t}$	$\oint_L \vec{H} \cdot d\vec{l} = I + \frac{d\Phi_D}{dt}$	prawo Ampere'a rozszerzone przez Maxwella	Przepływający prąd oraz zmienne pole elektryczne wytwarzają wirowe pole magnetyczne

gdzie:

E - pole elektryczne, [ V / m ]
H - pole magnetyczne, [ A / m ]
D - indukcja elektryczna, [ C / m²]
B - indukcja magnetyczna, [ T ]
F_D - strumień indukcji elektrycznej,
F_B - strumień indukcji magnetycznej,
j - gęstość prądu, [A/m²]
r - gęstość ładunku
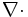$\nabla \cdot$ - operator dywergencji, [1/m],
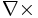$\nabla \times$ - operator rotacji, [1/m].

Pierwsze z równań - (dywergencja natężenia pola elektrycznego równa jest gęstości ładunku elektrycznego), postuluje, że strumień pola elektrycznego przechodzącego przez powierzchnię otaczającą ładunek jest proporcjonalny do wartości tego ładunku.
Strumień ten nie zależy od wielkości powierzchni ani od jej odległości od ładunku. Z tego wynika, że pole elektryczne ładunku musi być odwrotnie proporcjonalne do kwadratu odległości (powierzchnia przez którą przechodzi strumień rośnie wraz z kwadratem odległości). Jest to tzw. prawo Gaussa.

Z drugiego równania wynika, że zmienne w czasie pole magnetyczne wytwarza wirowe pole elektryczne (prawo indukcji Faradaya).

Z trzeciego równania wynika, że w przyrodzie nie istnieją ładunki magnetyczne (linie sił pola magnetycznego są zawsze zamknięte; w przypadku pola elektrycznego zaczynają i kończą się na ładunkach).