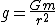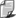 Prawo ciążenia
Prawo ciążenia
1. Prawo
powszechnego ciążenia
2. Siła grawitacji
3. Potencjał grawitacyjny, przyspieszenie grawitacyjne
i natężenie pola grawitacyjnego
4. Prędkości kosmiczne
5. Praca w polu grawitacyjnym
Co znaczą niektóre wzory:
m - masa ciała
G - stała grawitacji
R,r - odległość dwóch ciał ew. promień
Fg - ciężar ciała
g - przyspieszenie grawitacyjne
VI - pierwsza prędkość kosmiczna
VII - druga prędkość kosmiczna
1.
Prawo powszechnego ciążenia
Definicja: Grawitacja nazywana czasami
ciążeniem powszechnym to jedno z oddziaływań podstawowych
wyróżnianych przez fizykę. Oddziaływanie grawitacyjne
jest zależne od masy posiadanej przez poszczególne ciała
i od odległości między nimi.
2. Siła grawitacji
W ujęciu klasycznym, dwa ciała obdarowane masami M i
m, znajdujące się w odległości R od siebie, oddziaływują
na siebie siłą o wartości danej wzorem:
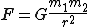
Wzór na przyspieszenie grawitacyjne:
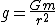
Wzór na przyspieszenie grawitacyjne
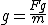
G to stała grawitacji, równa w przybliżeniu:
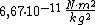
Siła grawitacji równa jest gradientowi energii potencjalnej:
3. Potencjał grawitacyjny,
przyspieszenie grawitacyjne i natężenie pola grawitacyjnego
A. Postać klasyczna
Porównując powyższy wzór do wzoru wynikającego z drugiej
zasady dynamiki Newtona, otrzymujemy wzór na przyspieszenie
grawitacyjne:
Jednostką przyspieszenia grawitacyjnego jest m×s-2 - czyli innymi słowy metr przez sekundę do kwadratu.
Natężenie pola grawitacyjnego to stosunek siły
grawitacyjnej, działającej na cało w polu grawitacyjnym,
do masy tego ciała:
Jednostką natężenia grawitacyjnego jest N×kg-1,
chociaż wzory na natężenie i przyspieszenie w polu
grawitacyjnym są sobie tożsame.
Potencjał grawitacyjny to wielkość skalarna,
wyrażająca się wzorem:
B Postać różniczkowa
Natężenie pola grawitacyjnego zdefiniowane jest jako
gradient potencjału grawitacyjnego:
Rozpiszmy powyższy wzór; pamiętajmy, że:
Zgodnie z definicją:
Aby obliczyć wartość wektora, posługujemy się Twierdzeniem
Pitagorasa:
Rozpatrując odległość od źródła pola w jednym wymiarze,
wartości wektorów w pozostałych wymiarach przyjmę
wartości zerowe
(y=0 ^ z=0)
4. Prędkości kosmiczne
I prędkość kosmiczna
Definicja: Pierwsza prędkość kosmiczna jest
to prędkość, jaką trzeba posiadać, aby móc orbitować
wokół ciała o znanej masie M po orbicie kołowej o
promieniu równym średniemu promieniowi tego ciała.
Pierwsza prędkość kosmiczna jest to prędkość,
jaką trzeba posiadać, aby móc orbitować wokół ciała
o znanej masie M po orbicie kołowej o promieniu
równym średniemu promieniowi tego ciała.
Prędkość ta dla Ziemi wynosi około 7,91km×s-1
Przykład zadania: Oblicz wartość pierwszej
prędkości kosmicznej dla Księżyca.
Druga prędkość kosmiczna:
Definicja: Druga prędkość kosmiczna jest
to najmniejsza prędkość, jaką trzeba posiadać, aby
móc uciec nieskończenie daleko od ciała o znanej masie
M. Ściślej - jest to najmniejsza prędkość, jaką nadać
trzeba ciału na powierzchni innego ciała o masie M,
aby tor jego ruchu stał się parabolą lub hiperbolą.
Drugą prędkość kosmiczną obliczamy, wykorzystując
zasadę zachowania energii. Porównujemy wartości energii
mechanicznej na powierzchni ciała i w nieskończoności:
Dla Ziemi wartość ta wynosi około 11,19km×s-1
Przykład zadania: Oblicz wartość drugiej
prędkości kosmicznej dla Księżyca.
5. Praca w polu grawitacyjnym
Praca w polu grawitacyjnym wykonana przez siłą
zewnętrzną przeciwko siłom grawitacji wyrażona może
zostać poprzez różnicę energii potencjalnych lub klasyczny
iloczyn siły przez pokonaną drogę:
W małej odległości od powierzchni Ziemi:
W odległości
porównywalnej z promieniem Ziemi:
Wyprowadzenie wzoru wymaga zastosowania rachunku całkowego:
Gdy ciało, mimo działania siły zewnętrznej skierowanej
przeciwko sile grawitacji zostaje opuszczone, wykonana
zostaje praca ujemna:
|