godzina...

Jednym z największych odkryć XX w. było odkrycie, że Wszechświat sie rozszerza. Zatem galaktyki, unoszone poprzez pęczniejącą przestrzeń, oddalają się od siebie. Natomiast to, w jaki sposób Wszechświat będzie dalej sie rozszerzał oraz czy proces ekspansji zostanie kiedykolwiek wyhamowany, zależy od ilości znajdującej się w nim materii.

Ilość materii we Wszechświecie wiąże się z jego geometrią. Związek pomiędzy materią a przestrzenią został określony w 1916 roku przez Alberta Einsteina w "Ogólnej Teorii Względności". Zależność tą można przedstawić za pomocą układu skomplikowanych równań różniczkowych :

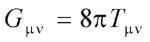
Lewa strona powyższego równania przedstawia obiekt matematyczny, zbudowany wyłącznie z wielkości, które opisują geometrię przestrzeni. Obiekt matematyczny stojący z prawej strony opisuje rodzaj, ilość, ruch oraz rozłożenie w przestrzeni materii. W celu scharakteryzowania budowy Wszechświata oraz określenia jego przyszłości można wykorzystać jeden z poniższych sposobów:

• wyznaczając wszystkie formy materii we Wszechświecie, zbudować obiekt matematyczny opsiujący materię, po czym ostatecznie rozwiązując równania wyznaczyć geometrię Wszechświata
• wyznaczyć geometrię Wszechświata bezpośrednio z obserwacji, a na tej podstawie wyznaczyć ilość i rodzaj materii znajdującej się we Wszechświecie

Każdemu z nas geometria kojarzy się z systemem stworzonym jeszcze w Starożytności przez Euklidesa. Ponieważ na codzień posługujemy się nią, mało kto zdaje sobię sprawę z tego, że mogą istnieć inne geometrie o całkeim odmiennych własnościach metrycznych. Przykładami dwuwymiarowych przestrzeni, w których własności metryczne są inne niż w geometrii euklidesowej są:

• powierzchnia sfery - zakrzywiona dodatnio, suma kątów w trójkącie rozpiętym na takiej powierzchni jest większa od 180 ° (rys. 2)
• powierzchnia tzw. "małpiego siodła" - zakrzywiona ujemnie, trójkąt rozpięty na takiej powierzchni będzie posiadał sumę kątów mniejszą od 180 ° (rys. 3)

Badana powierzchnia staje się zakrzywiona dopiero w momencie, gdy jej rozmiar jest porównywalny z promieniem krzywizny. Podobnie było z powierzchnią Ziemi, która przez długie lata kojarzyła się ludziom jako płaska, ponieważ poruszali się oni w obszarach małych w porównaniu do promienia Ziemi. Analogicznie sytuacja wygląda z trójwymiarową przestrzenią - przebywamy w obszarach stosunkowo małych w porównaniu do promienia krzywizny całego Wszechświata, w związku z czym nasze przekonanie o tym, że Wszechświat nie jest zakrzywiony może być mylne. Aby wykryć zatem krzywiznę Wszechświata niezbędne jest badanie bardzo dużych obszarów.

Dynamika Wszechświata, czyli to w jaki sposób będzie się on rozszerzał, związana jest zarówno z geometrią, jak i ilością materii we Wszechświeci (rys. 4). Możemy wyróżnić trzy możliwe przypadki przyszłych losów Wszechświata:

• Wszechświat się rozszerza, a następnie kurczy - odległość między wybranymi galaktykami rośnie do pewnej maksymalnej wartości, po czym zaczyna maleć aż do zera - jest to przypadek, kiedy materii we Wszechświecie jest na tyle dużo, aby jej samograwitacja mogła wyhamować ekspansję i spowodować proces odwrotny - kurczenie się Wszechświata. Geometria Wszechświata jest sferyczna, Wszechświat jest zamknięty, ma skończoną objętość, ilość materii jest również skończona
• Wszechświat rozszerza się do nieskończoności - odległość między wybranymi galaktykami rośnie do nieskończoności - przypadek, w którym Wszechświat wypełnia mała ilość materii, której samograwitacja jest zbyt słaba by zahamować proces rozszerzania się. Geometria Wszechświata odpowiada ujemnej krzywiźnie, jego objętość oraz ilość materii znajdującej się w nim jest nieskończona
• Wszechświat rozszerza się nieustannie, ale prędkość rozszerzania będzie malała do zera w nieskończonej skali czasowej - przypadek, w którym średnia gęstość materii we Wszechświecie jest ściśle określona, wynosi ok. 10^-29g/cm³ jego objętość oraz ilość materii znajdującej się w nim jest nieskończona