Podstawowy wzór teorii kinetycznej gazu doskonałego

Powiązanie wartości ciśnienia gazu z prędkościami cząstek nie przedstawia problemu. W podręcznikach spotyka się "sześcienną" i "kulistą" wersja wyprowadzenia. Przedstawimy je obie.

Wyprowadzenie - wersja A. Gaz w sześciennym pudełku

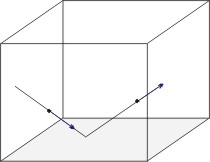
Rozważmy gaz - zespół cząsteczek chaotycznie poruszających się w pudle - sześcianie o krawędzi l. Podczas sprężystych zderzeń zderzeń z wybrana - powiedzmy "dolną poziomą" - ścianką zmienia się na przeciwną składowa prędkości prostopadła do ścianki, dwie pozostałe składowe - lezące w płaszczyźnie ścianki - nie ulegają zmianie.

Wektory pędu i cząsteczki przed i po zderzeniu możemy zapisać:

p_przed = ( mv_x , mv_y , mv_z )

p_po = ( mv_x , mv_{y ,} - mv_z)

co ilustruje poniższy rysunek.

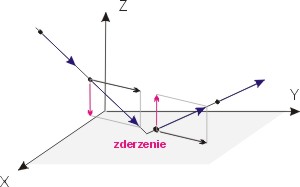
Zmiana pędu  dana jest przez:

Δp = p_po - p_przed = (0, 0, - 2mv_z)

a więc ma tylko jedna składową i jej wartość równa jest

Δp = -2mv_z

Druga zasada dynamiki daje natychmiast wartość siły działającej na cząstkę:

F =(Δp/Δt) = -2mv_z / Δt

Znak oznacza tu, że siła działająca na cząsteczkę skierowana jest "od ścianki". 

Trzecia zasada dynamiki pozwala zauważyć, że siła, z jaka cząsteczka działa na ściankę równa jest: 

F = 2mv_z /Δt

Jaką wartość czasu przyjąć? Gdybyśmy byli zainteresowani wartością chwilowych sił działających w momencie oddziaływania - za Δt przyjęlibyśmy czas zderzenia. Interesuje nas jednak uśredniona w czasie siła,  z jaką cząsteczka działa na ściankę. Jak często powtarzają się takie zderzenia? Co jaki okres czasu maja one miejsce? Czas między zderzeniami to czas potrzebny do przebycie przez cząsteczkę drogi "tam i z powrotem" pomiędzy ściankami naczynia:  Δt = 2l/v_z , i takiej wartości czasu użyjemy obliczając średnia wartość siły.

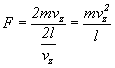
Tyle od jednej cząsteczki. Sumując wkład od wszystkich cząsteczek otrzymamy

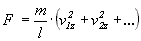
W nawiasie sumujemy tu kwadraty z-owej składowej wszystkich cząsteczek. Prawą stronę podzielimy i pomnożymy przez liczbę cząsteczek N

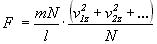
Łatwo widać, że drugi ułamek jest po prostu średnią kwadtatu z-owej składowej prędkości w całym zespole

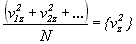
Wzór na siłę przybiera postać:

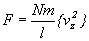
Ciśnienie z kolei jest stosunkiem siły działającej na powierzchnię ( w naszym przypadku ściankę) do pola tej powierzchni (u nas kwadratowa ściana sześcianu ma pole S = l²)

p = F / S = Nm{v_z²} / l³  = M/V {v_z²}= r {v_z²}  .

 Pozostaje uwolnić się od wybranego do rozważań kierunku z. Dla każdej cząsteczki mamy v² = v_x² + v_y² + v_z², co dla średniej w zespole daje 

{v²} = {v_x²} + {v_y²} + {v_z²}

A ponieważ żaden kierunek nie jest wyróżniony i średnie prędkości we wszystkich kierunkach są równe więc {v_x²} = {v_y²} = {v_z²} . Możemy napisać:

{v²} = {v_z²} + {v_z²} + {v_z²} = 3{v_z²}

czyli 

{v_z²} = 1/3 {v²}

Wzór na ciśnienie da się więc - co należało pokazać - zapisać:

p = 1/3 r {v²}

Wyprowadzenie - wersja B. Gaz w kulistym naczyniu

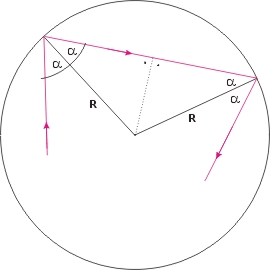
Rozważmy gaz doskonały zamknięty w naczyniu o kształcie kuli o promieniu R. Cząsteczka gazu uderzając o ścianę naczynia zmienia swój pęd, a konkretnie - zmienia zwrot radialnej składowej pędu (skierowanej wzdłuż promienia). Jej wartość przez zderzeniem równa jest p_r = mvcosα,  a zmiana pędu w trakcie zderzenia wynosi Δp = -2mvcosα. Czas, w którym (średnio) dokonuje się taka zmiana pędu to czas potrzebny na przebycie drogi pomiędzy kolejnymi miejscami zderzeń. Na rysunku widać, że droga ta jest równa s = 2Rcosα, a co za tym idzie czas Δt = 2Rcosα/v.

Druga zasada dynamiki daje wartość siły: 

F = Δp/Δt = mv²/R. 

Na marginesie - ciekawe, że jest to wartość siły dośrodkowej dla cząsteczki poruszającej się z prędkością v po wielkim kole naszego naczynia. 

Suma sił pochodzących od wszystkich N cząsteczek dana jest wiec przez sumę po wszystkich cząsteczkach:

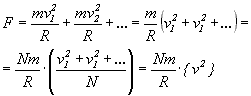
gdzie {v²} jest średnią wartością kwadratu prędkości cząsteczek w zespole 

 {v²} = (v₁² + v₂² + v₃² + ... ) / N

Siłę można więc zapisać w postaci

F = M {v²} / R

gdzie M = Nm oznacza masę całego gazu. Aby otrzymać ciśnienie dzielimy wartość siły przez powierzchnię naczynie S = 4pR²

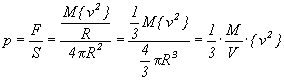
czyli ostatecznie

p = 1/3 r {v²}