::: Iwiedza ::: - Ty tu rządzisz!

Praca gazu

jak gaz wykonuje pracę i obliczanie pracy gazu.

Jak gaz wykonuje pracę

Czy gaz może wykonać pracę? Przyjrzyjmy się poniższym sytuacjom.

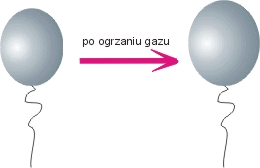
1. Balon napełniony gazem (na przyład powietrzem) zwiększa swoją objętość po podgrzaniu zawartości. Do rozciągnięcia gumy z której jest on zrobiony potrzebna jest pewna praca. Wykonał ją rozprężający się gaz.
2. Gaz zamknięty jest pod mogącym się swobodnie poruszać, obciążonym tłokiem. Po ogrzaniu gaz rozprężając się podnosi tłok i leżący na nim odważnik a podnosząc odważnika wykonuje pracę.

Widać, że wykonywanie pracy przez gaz związane jest z rozprężaniem, czyli zwiększeniem objętości gazu. Wypada jednak powiedzieć, że istnieją procesy, w trakcie których gaz zwiększając objetość nie wykonuje pracy (np. swobodne rozprężanie w próżnię).

Obliczanie pracy gazu

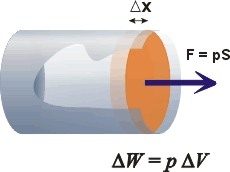
Przyjrzyjmy się cylindrowi z ruchomym tłokiem. Gaz zamknięty w cylindrze działa pewnym ciśnieniem na wszystkie ścianki. Działa też na wybraną przez nas ruchomą ściankę (kolor pomarańczowy).

Całkowita siła z jaką gaz działa na ściankę równa jest (z definicji ciśnienia)

F = p S

gdzie p oznacza ciśnienie gazu, a S pole powierzchni ścianki.

Jeśli teraz (na skutek ogrzewania) gaz rozprężając się przesunie nieco ściankę (o Δx) to wykona pracę. Jej wartość łatwo obliczyć.

ΔW = F Δx = p S Δx

Siła - zakładamy - podczas tego niewielkiego przesunięcia była stała.

Jednak S·Δx jest po prostu zmainą objętości gazu ΔV, więc praca wykonana przez gaz równa jest

ΔW = p ΔV

Wzór ten słuszny jest tam, gdzie ciśnienie się nie zmienia. Słuszny jest więc dla procesów, w których zmiana ciśnienia jest znikoma. Mówimy czasem, że pΔV to praca elementarna.

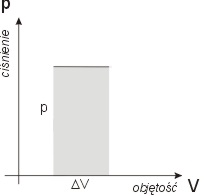
W zmiennych [p,V] wartość pracy to po prostu pole pod wykresem.

pole = pΔV = W

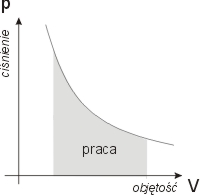
W przypadku procesu, w którym ciśnienie gazu uległo zmianie wartość pracy równa jest polu powierzchni pod krzywą p = p(V)

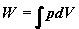Można też obliczać pracę wykonaną przez gaz w jakimś procesie korzystając z pierwszej zasady termodynamiki. Otrzymujemy

ΔW = ΔU - ΔQ