Praca gazu doskonałego

Najłatwiej obliczyć pracę w procesie izochorycznym. Gaz nie zmienia objętości. Ponieważ  DV = 0  więc pΔV = 0  czyli 

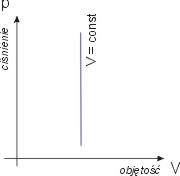
W = 0

W stałej objętości gaz nie wykonuje więc pracy.

W procesie izobarycznym, czyli pod stałym ciśnieniem, mamy od razu wynik 

W = p ΔV

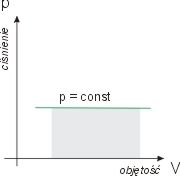
Równanie Clapeyrona daje przy stałym ciśnieniu  pΔV = nR ΔT  stąd

W = nR ΔT

W procesie izotermicznym a więc w stałej temperaturze pole pod krzywą p = p(V) = nRT/V równe jest

W = nRT ln( V₂/ V₁ )

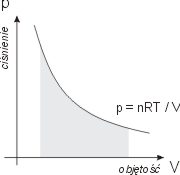
co można (używając prawa Bolyle'a-Mariotte'a) zapisać

W = nRT ln( p₁/ p₂ )

W procesie adiabatycznym (bez wymiany ciepła) obliczanie pracy jako pola pod krzywą ciśnienia daje

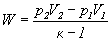
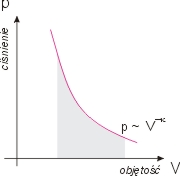
Jak pamiętamy jest tzw. wykładnikiem adiabaty, równym stosunkowi ciepła molowego pod stałym ciśnieniem do ciepła molowego gazu w stałej objętości.

k = C_p/C_v

 Wynik ten można też otrzymać na podstawie pierwszej zasady termodynamiki  ΔW = ΔU - ΔQ = ΔU = nC_VΔT  i równania Clapeyrona, które daje Δ (pV) = n R ΔT. Otrzymujemy

 W = n C_V ΔT

W = C_V Δ( pV ) / R

W = C_V ( p₂V₂ - p₁V₁ ) / R

Co można przekształcać dalej...