 Proces adiabatyczny
Proces adiabatyczny
okreslenie
równanie
stanu: prawo Poissona
wykresy
zmiany
energi wewnętrznej
uwagi
Określenie
Proces adiabatyczny to
proces, w którym gaz nie wymienia ciepła
z otoczeniem
Proces taki zachodzi w układzie dobrze
izolowanym termicznie, albo gdy przeprowadzony
zostanie na tyle szybko, by gaz nie
zdążył wymienić ciepła z otoczeniem.
Równanie stanu:prawo Poissona
Otrzymanie równania wiążącego ze sobą
parametry gazu w procesie adiabatycznym
wymaga znajomości rachunku różniczkowego
i całkowego. Podamy je bez wyprowadzenia:
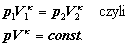
W powyższym związku, zwanym równaniem
Poissona, indeksy 1 i 2 oznaczają
początkowy i końcowy stan gazu, a wykładnik k
(czytaj 'kappa'), nazywany wykładnikiem adiabaty, równy
jest stosunkowi ciepła molowego gazu
w procesie izobarycznym do ciepła molowego
gazu w procesie izochorycznym:
k
= CP/CV = (i+2)/i
Tą samą zależność można przedstawić
w innych zmiennych. W tym celu rugujemy
p (ciśnienie) bądź V (objętość gazu)
z równania Poissona (przy pomocy równania
ClapeyronapV
= nRT ). Otrzymujemy wówczas:
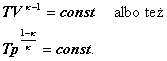
W procesie adiabatycznym zmieniają
się więc wszystkie parametry gazu: ciśnienie,
objetość i temperatura. Podczas adiabatycznego sprężania gazu jego ciśnienie
i temperatura rosną. Podczas adiabatycznego
rozprężania ciśnienie zmniejsza się
a gaz się ochładza.
Wykresy
Równanie stanu pVk = const daje:
p = const / V-k
Określa to zależność ciśnienia od objętości.
Wykresem procesu izotermicznego w zmiennych
(p,V) jest krzywa potęgowa.
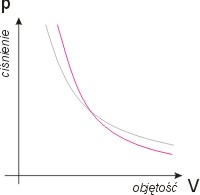
Rysunek
obok ukazuje adiabatę (kolor czerwony)
w porównaniu z izotermą (kolor szary).
Adiabata ma bardziej stromy przebieg,
tym bardziej stromy im większy jest
wykładnik adiabatyk.
Asymptotami tej krzywej są proste p=0
i V=0.
Również sporządzając wykresy w innych
zmiennych zmiennych mamy do czynienia
z funkcją potęgową:
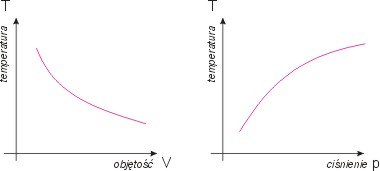
Zmiany energii wewnętrznej
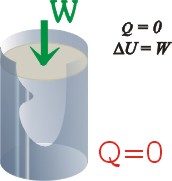
W procesie adiabatycznym gaz
nie wymienia ciepła z otoczeniem:
DQ
= 0
Zmiany energii wewnętrznej zachodzą
jedynie na drodze pracy. Pierwsza zasada
termodynamiki daje więc:
DU
= DW
Znajomość wzoru na energię wewnętrzną
gazu doskonałego U = nCVT pozwala na obliczenie stąd pracy:
DW
= DU = nCVDT
co - korzystając z równania Clapeyrona
- można zapisać jako:
DW
= CVD(pV) / R
Zastosowanie znanych zależności pomiędzy
CV i k pozwala z powyższych zależności
otrzymać na przykład:
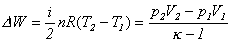
Proces adiabatyczny przeprowadzony
przez szereg stanów równowagowych
(czyli
kwazistatycznie) jest procesem, w którym
zmiana entropii jest zerowa:
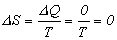
Entropia nie ulega zmianie. Taki proces
jest wówczas procesem izoentropowym,
co tłumaczy umieszczenie adiabaty wśród izoprocesów
gazu doskonałego.
Uwagi
Fakt, że w trakcie adiabatycznego sprężania
(i rozprężania) gaz zmienia temperaturę
znalazł
liczne zastosowania praktyczne.
W silniku wysokoprężnym Diesela adiabatyczne
(bo bardzo szybkie) sprężenie mieszanki
powoduje podniesienie jej temperatury
do temperatury
samoczynnego zapłonu.
Adiabatyczne rozprężanie gazu wykorzystuje między innymi w chłodziarkach
sprężarkowych; jest ono podstawą jednej
z metod skraplania gazów (metoda Hampsona-Lindego).
|