Proces izobaryczny

okreslenie
równanie stanu: prawo Gay-Lussaca
wykresy
zmiany energi wewnętrznej

Określenie

Proces izobaryczny to proces, w którym ciśnienie gazu pozostaje stałe

p = const

Proces izobaryczny inczej nazywany jest przemianą izobaryczną lub w skrócie - izobarą. Jest jednym z izoprocesów gazu doskonałego

Równanie stanu: prawo Gay – Lussaca

Stałość ciśnienia pozwala otrzymać z równania Clapeyrona prostszą postać równania stanu. Rozważmy w tym celu proces izobaryczny prowadzący ze stanu (1) do stanu (2). Napiszmy „dwa” równania Clapeyrona: dla gazu przed, i po przeprowadzeniu procesu:

p₁V₁ = n₁RT₁

p₂V₂ = n₂RT₂

Jest to jednak ten sam gaz, czyli n₂ = n^­₁, a ponadto ciśnienie końcowe równe jest (z definicji procesu) ciśnieniu początkowemu, więc p₂ = p₁. Opuszczając zbędne indeksy otrzymujemy:

pV₁ = nRT₁

pV₂ = nRT₂,

czyli

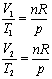
Prawe strony wzorów są sobie równe a ponadto stałe , więc i lewe strony muszą być sobie równe. Napiszemy:

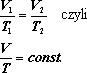
W trakcie przeprowadzania procesu izobarycznego stosunek objętości do temperatury jest stały; objętość i temperatura są w tym procesie wielkościami proporcjonalnymi. 

Otrzymana przez nas zależność stanowi treść prawa Gay – Lussaca, uzyskanego pierwotnie na drodze empirycznej - jako uogólnienie danych doświadczalnych. 

Odejmując stronami równania Clapeyrona, zauważamy mimochodem, że w tym procesie 

pDV = nRDT

Prawo Gay-Lussaca można wyrazić przy użyciu innych zmiennych, np. gęstości r czy koncentracji a :

Ponieważ r = m/V, więc V = m/ r. Po podstawieniu ostatniej zależności do równania stanu otrzymujemy:

m/rT = const

rT = const/m

Masa gazu jest jednak stała – nie ubywa go ani nie przybywa, więc ostatecznie

r T = const

To samo postępowanie daje dla koncentracji (a = N/V):

aT = const

Wykresy

Jeśi V/T = const, to V = const · T. Objętość jest więc liniową funkcją temperatury i wykresem procesu izochorycznego w zmiennych (V,T) jest prosta. Wartość współczynnika kierunkowego tej prostej otrzymujemy wprost z równania Clapeyrona:

V = (nR/p) · T

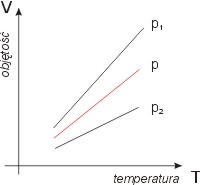
Na rysunku obok widzimy wykres izobary dla różnych ciśnień, przy czym p₁ < p < p₂.

Nie doprowadzamy tych prostych do punktu (T=0, V=0) wiedząc, że tych warunkach nasz model - gaz doskonały - nie opisuje rzeczywistości.

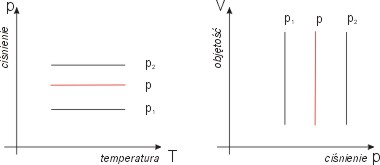
W pozostałych zmiennych wykres izobary nie wymaga komentarza. Jest nim prosta prostopadła do osi ciśnienia (p = const):

Zmiany energii wewnętrznej

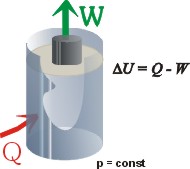W procesie izobarycznym (pod stałym ciśnieniem) wyrażenie na pracę wykonaną przez gaz jest szczególnie proste:

DW = pDV

co (jak pokazaliśmy wyżej rozważając równanie stanu) jest równoważne 

DW = nR DT

Ciepło pobrane przez gaz dane jest przez

DQ = nC_P DT

lub, używając ciepła właściwego

DQ =mc_P DT

przy czym pamiętamy, że ciepło molowe gazu doskonałego w procesie izobarycznym równe jest

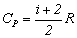
gdzie i oznacza tzw. liczbę stopni swobody cząsteczki gazu.

Pierwsza zasada termodynamiki daje więc na przykład:

DU = DQ + DW =

= nC_PDT - p DV = nC_PDT - nRDT = n (C_P-R)DT

a po uwzględnieniu, że C_P-R = C_V

DU = nC_VDT

czyli tak, jak samo jak w przypadku izochory. Czy wiesz dlaczego?

Można też uzyskać np.:
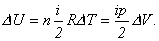