Proces izotermiczny

okreslenie
równanie stanu: prawo Boyle'a - Mariotte'a
wykresy
zmiany energi wewnętrznej
uwagi

Określenie

Proces izotermiczny to proces, w którym temperatura gazu pozostaje stała

T = const

Proces izotermiczny inaczej nazywany jest przemianą izotermiczną lub w skrócie - izotermą. Jest jednym z izoprocesów gazu doskonałego

Równanie stanu: prawo Boyle'a - Mariotte'a

Parametrami mogącymi się zmieniać w tym procesie są objętość V i ciśnieniep. Nie mogą one się jednak zmieniać niezależnie. Stałość temperatury pozwala otrzymać z równania Clapeyrona prostszą postać równania stanu. Rozważmy w tym celu proces izotermiczny prowadzący ze stanu (1) do stanu (2). Napiszmy „dwa” równania Clapeyrona: dla gazu przed, i po przeprowadzeniu procesu:

p₁V₁ = n₁RT₁

p₂V₂ = n₂RT₂

Jest to jednak ta sama ilość gazu, nie pozwalamy na ucieczkę cząsteczek ani nie wprowadzamy nowych, więc n₂ = n^­₁ , a ponadto temperatura końcowa T₂równa jest (z definicji procesu) temperaturze początkowej T₁, więc T₂ = T₁. Opuszczając zbędne indeksy przy n i T otrzymujemy:

p₁V₁ = nRT

p₂V₂ = nRT

Prawe strony wzorów są sobie równe a ponadto stałe, więc i lewe strony muszą być sobie równe. Napiszemy:

p₁V₁ = p₂V₂

Ponieważ stany (1) i (2) mogą być dowolnymi stanami podczas procesu, wnioskujemy że

pV = const.

A więc w trakcie przeprowadzania procesu izotermicznego iloczyn ciśnienia i objętości jest stały; ciśnienie i temperatura są w tym procesie wielkościami odwrotnie proporcjonalnymi.

Otrzymane przez nas zależności stanowią treść prawa Boyle’e – Mariotte’a, uzyskanego pierwotnie na drodze empirycznej - jako uogólnienie danych doświadczalnych.

Prawo Boyle'e-Mariotte'a można wyrazić przy użyciu innych zmiennych, np. gęstości czy koncentracji:

Ponieważ gęstośćr = m/V, więc V = m/r. Po podstawieniu ostatniej zależności do równania stanu otrzymujemy:

pm/r = const.

p/r = const/m

Masa gazu jest jednak również stała – nie ubywa go ani nie przybywa, więc ostatecznie

p/r = const

To samo postępowanie daje dla koncentracji (a= N/V)

p/a = const.

Wykresy

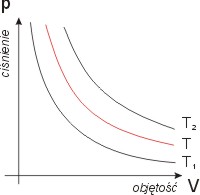
Równanie stanu pV = const daje:

p = const / V  =  (nRT) / V

Określa to zależność ciśnienia od objętości. Wykresem procesu izotermicznego w zmiennych (p,V) jest hiperbola. Asymptotami tej hiperboli są proste p=0 i V=0. 

Na rysunku obok widzimy wykres izotermy dla różnych temperatur, przy czym T₁ < T < T₂.

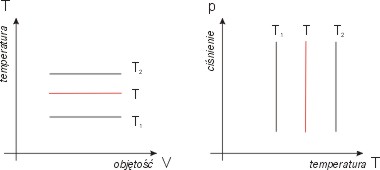
W pozostałych zmiennych wykres izotermy nie wymaga komentarza. Jest nim prosta prostopadła do osi temperatury (T = const):

Zmiany energii wewnętrznej

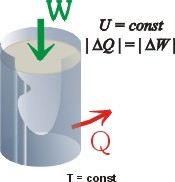
W procesie izotermicznym temperatura gazu nie zmienia się, a ponieważ energia wewnętrzna gazu doskonałego zależy wyłącznie od temperatury, więc w procesie izotermicznym energia wewnętrzna gazu doskonałego nie zmienia się

U = const .   czyli     DU = 0

Pierwsza zasada termodynamiki daje: DU = DQ + DW = 0, zatem