Gaz doskonały

mikroskopowa i makroskopowa gazu doskonałego
równanie stanu - równanie Clapeyrona,
energia wewnętrzna
granice stosowalności modelu.

Gaz doskonały definiować można zarówno na poziomie mikroskopowym (przez podanie właściwości elementów, z których jest zbudowany), jak i na poziomie makroskopowym (poprzez podanie jego właściwości jako całości). Poniżej podamy obie te definicje

Definicja mikroskopowa

1. Gaz składa się z cząsteczek, które traktować można jak punkty materialne. Łączna objętość wszystkich cząsteczek gazu jest więc pomijalna. Zależnie od rodzaju gazu, cząsteczka może być atomem lub związana grupą atomów. Z punktu widzenia chemii cząsteczki gazu to cząsteczki pierwiastka lub związku chemicznego. Wszystkie one są identyczne.
2. Cząsteczki podlegają prawom mechaniki Newtona.
3. Całkowita liczba cząsteczek jest bardzo duża. Cząsteczki poruszają się chaotycznie we wszystkich kierunkach, zderzają ze ściankami naczynia i ze sobą nawzajem. Niezależnie od losów poszczególnych cząsteczek, o zachowaniu gazu w skali makro decydują średnie wartości całego zespołu.
4. Cząsteczki zdarzają się ze sobą sprężyście, wymieniają pęd bez strat energii.
5. Poza momentami zderzeń cząsteczki nie oddziałują ze sobą, a czas trwania tych zderzeń jest pomijalnie mały. Zakładamy tym samym mały - w porównaniu z rozmiarami cząsteczek - zasięg sił oddziaływania międzycząsteczkowego. Znaczy to też że pomiędzy zderzeniami cząsteczki poruszają się ruchem jednostajnym prostoliniowym.

Definicja mikroskopowa określa więc gaz doskonały jako zespół cząsteczek o szczególnych własnościach. Podane tu elementy definicji są punktem wyjścia kinetycznej teorii gazu.

Definicja makroskopowa (termodynamiczna)

Za gaz doskonały uważać będziemy gaz spełniający łącznie prawa Boyle'a-Mariotte'a, Gay-Luusaca i Charlesa, czyli gaz dla którego w stałej temperaturze iloczyn objętość i ciśnienie są odwrotnie proporcjonalne, dla określonej objętości ma stały stosunek ciśnienia do temperatury jest stały, a pod stałym ciśnieniem - proporcjonalne są objętość i temperatura. Łącznie możemy to zapisać jedną zależnością:

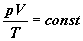
Powyższy związek, definiujący gaz doskonały w ujęciu makroskopowym dotyczy oczywiście ustalonej ilości materii (ustalona masa, ustalona liczba cząsteczek, ustalona liczba moli gazu)

Definicja ta określa związek pomiędzy parametrami termodynamicznymi gazu - a więc określa gaz doskonały poprzez jego równanie stanu.

Równanie stanu - równanie Clapeyrona

Pełna postać równania stanu gazu doskonałego jest następująca:

p V = n R T

i nazywane jest ono równaniem Clapeyrona. Przy czym p oznacza ciśnienie gazu, V - objetość, T - temperaturę, n - liczbę moli gazu a R jest tzw. stałą gazową równą R = 8, 314 J/mol·K.

Nic nie przeszkodzi, używając związku R = N_A k zapisać równania następująco:

p V = N k T

gdzie k = R / N_A jest stałą Boltzmanna

Na uwagę zasługuje fakt, że wymiarem prawej (i lewej) strony jest wymiar energii.

Równanie stanu w innych zmiennych

Równanie Clapeyrona wiąże ze sobą występujące w nim wielkości, lecz można wyrazić je w innych zmiennych. Pamiętając, że gęstość r = m/V, a masa m = nm , gdzie m oznacza masę jednego mola otrzymujemy r = nm/V czyli V = nm/r , .a po wstawieniu tak wyrażonej objętości do równania stanu mamy jego równoważną postać:

.

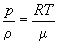Można też użyć koncentracji cząstek a = N/V. Objętość możemy zapisać jako V = N/a. Ponadto liczba moli n = N/N_A , wiec równanie stanu przybiera postać:

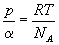
Obydwie powyższe postacie wiążą ze sobą wyłącznie wielkości intensywne i maja charakter "lokalny". O powiązanie ze sobą wielkości ekstensywnych pokusimy się kiedy indziej, używając pojęcia entropii

Użyteczna zależność

Przeprowadzając dowolny proces z udziałem stałej ilości gazu doskonałego możemy napisać równanie Clapeyrona dla stanu początkowego (1) i końcowego (2):

p₁ V₁ = n R T₁

p₂ V₂ = n R T₂

a po odjęciu stronami pierwszego od drugiego otrzymujemy

p₂V₂ - p₁V₁ = n R ( T₂ - T₁ )

czyli

D (pV) = n R DT

Energia wewnętrzna gazu doskonałego

Poszukując wyrażenia na energię wewnętrzną gazu doskonałego zauważmy najpierw, że - zgodnie z wynikami teorii kinetycznej energia wewnętrzna gazu doskonałego zależy wyłącznie od temperatury gazu, tzn. dla określonej masy gazu jest jednakowa dla wszystkich stanów gazu o jednakowej temperaturze.

Wyrażenie na energię wewnętrzną gazu doskonałego otrzymamy analizując ogrzewanie gazu w stałej objętości, bo to najprostsze. Gaz nie wykonuje wówczas pracy DW = p DV = 0. Pierwsza zasada termodynamiki daje DU = DQ + DW = DQ + 0, czyli DU = DQ. Zastosowanie definicyjnego wzoru na ciepło molowe prowadzi do:

DU = n C_V DT

co - używając równania Clapeyrona - da się zapisać w postaci:

DU = C_V D( pV ) / R

DU = C_V ( p₂V₂ - p₁V₁ ) / R

Zależność ta - podkreślmy - jest słuszna nie tylko dla izochory, lecz dla dowolnego procesu stałej masy gazu, w którym temperatura zmienia się o DT .

Zmiana energii wewnętrznej w wybranym przez nas procesie o stałej objętości (a-A) jest taka sama jak w procesie przebiegającym pod stałym ciśnieniem (a-B), taka jak w procesie adiabatycznym (b-A) i w ogóle taka sama dla wszystkich procesów prowadzących od temperatury T₁do T₂.

Przyjmują za temperaturę początkową T = 0 K możemy to zapisać:

U - U₀ = n C_V T ,

czyli

U = n C_V T + U₀ ,

gdzie U₀ jest stałą równą wartości energii wewnętrznej w temperaturze 0K. Rozsądnie jest przyjąć ją równą zeru.Otrzymujemy ogólny wzór na energię wewnętrzną gazu doskonałego:

U = n C_V T

Granice stosowalności modelu

Jak każdy model rzeczywistości - tak i gaz doskonały podlega pewnym ograniczeniom i w pewnych warunkach przestaje się sprawdzać. O ile w normalnych warunkach model gazu doskonałego pozwala uzyskiwać wyniki zbliżone do doświadczalnych (dla większości gazów), o tyle zawodzi zdecydowanie dla niskich temperatur i dużych gęstości, nie przewidując zmian stanu skupienia (skraplanie).