Gazy rzeczywiste
równanie Van der Waalsa
inne równania dwuparametrowe

Gazy doskonałe nie istnieją.

Model, jakim jest gaz doskonały, pozwala na proste rachunki i sprawdza się dość dobrze w pewnych warunkach. Jednak cierpi braki zarówno co do realizmu założeń, jak i co do opisu zachowania się gazów. Założenia, które posłużyły do budowy modelu gazu doskonałego w pewnych warunkach tracą sensowność. Postulat zerowej objętości cząsteczek gazu nie daje się obronić, podobnie jak założenie że cząsteczki nie oddziałują ze sobą. W efekcie model gazu doskonałego nie opisuje poprawnie rzeczywistości. Wartości doświadczalne odbiegają od przewidywań teorii.

Co gorsza, poza niedociągnięciami ilościowymi, model ten ponosi klęskę jakościową. Zawodzi całkowicie w tych warunkach, gdzie objętości cząsteczek staje się porównywalna z objętością zajmowana przez gaz (gdy na skutek koncentracji cząsteczek odległości między nimi stają się porównywalne z ich rozmiarami). Według równania Clapeyrona w temperaturze dążącej do zera bezwzględnego objętość gazu pod stałym ciśnieniem malałaby do zera. Tak się jednak nie dzieje, bo gaz najczęściej w takich warunkach nie jest już gazem... Mówimy tu o przejściach fazowych (skraplanie gazu w niskich temperaturach i wysokich ciśnieniach), których to przejść model wcale nie przewiduje.

Zbudowano więc modele pozwalające - przynajmniej częściowo - uwzględnić takie fakty jak niezerowa objętość cząsteczek gazu i istnienie oddziaływań między cząsteczkami. Są one dobrym przybliżeniem rzeczywistości w szerszym zakresie ciśnień i temperatur, choć nie znamy równania słusznego dla każdego gazu w każdych warunkach. Poniżej kilka najbardziej popularnych równań stanu:

Równanie Van der Waalsa

Ma ono postać

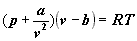
gdzie
p jest ciśnieniem gazu,
v jest objętością molową v = V/n lub po prostu objętością jednego mola gazu,
R to uniwersalna stała gazowa,
T jest temperaturą bezwzględną (mierzoną w kelwinach),
natomiast a i b to stałe, wyznaczane zresztą na drodze doświadczalnej dla każdego gazu.

Jak widać, do równania Clapeyrona, zapisanego przy użyciu objętości molowej

pv = RT

wprowadzone zostały poprawki - poprawka do ciśnienia (+ a/V² ) i poprawka do objętości (- b).

Poprawka do ciśnienia ma odzwierciedlać przyciąganie między cząsteczkami gazu dla większych odległości.

Poprawka do objętości to próba uwzględnienia objętości własnej cząsteczek gazu (ściślej mówiąc - sił odpychania na małych odległościach).

Gaz opisywany tym równaniem nazywany bywa gazem Van der Waalsa. Sukcesem tego modelu jest to, że daje pewne wskazówki co do przejść fazowych (skraplanie gazu) i postuluje nieściśliwość cieczy (nieskończony wzrost ciśnienia dla objętości gazu zbliżającej się do objętości własnej cząsteczek).

Oczywiście możemy również użyć "zwykłej" objętości. Podstawiając zależność v = V/n trzymamy:

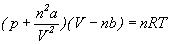
Wartości stałych a i b można uzyskać dopasowując krzywe doświadczalne lub z wartości tzw. parametrów krytycznych gazu:

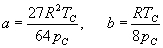
Inne równania dwuparametrowe

Wychodzącym z użycia dwuparametrowym równaniem jest prosta modyfikacja równania Van der Waalsa - równanie Berthelota:

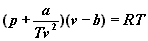
Jest ono dokładniejsze od równania Van der Waalsa dzięki uwzględnieniu faktu, że poprawka ciśnienia (+ a/TV² ) maleje wraz ze wzrostem temperatury. Jest tak dlatego, że energia potencjalna dalekich oddziaływań cząsteczek jest wtedy znikomo mała w porównaniu z energią kinetyczną cząstek.

Dokładniejszym równaniem, bodaj najlepszym spośród równań o dwu parametrach jest równanie Redlich-Kwonga. Ma ono postać

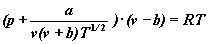
czyli - inaczej pisząc

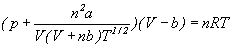
przy czym, podobnie jak w równaniu Van der Waalsa
p jest ciśnieniem gazu,
v jest objętością molową v = V/n lub po prostu objętością jednego mola gazu,
R to uniwersalna stała gazowa,
T jest temperaturą bezwzględną (mierzoną w kelwinach),
natomiast a i b to stałe, lecz różne od stałych z równania Van der Waalsa.

Używane bywa również dwuparametrowe równanie Dietericiego:

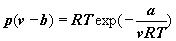
i wiele innych.