Kinetyczna teoria gazu doskonałego

czym jest teoria kinetyczna,
ciśnienie gazu a kinematyka cząsteczek
temperatura gazu, interpretacja kinetyczna,
energia wewnętrzna i ciepło właściwe gazu jednoatomowego
zasada ekwipartycji energii
energia wewnętrzna i ciepło właściwe gazów wieloatomowych

Czym jest teoria kinetyczna gazu

Teoria kinetyczna gazu (nazywana też teorią kinetyczno-molekularną albo kinetyczno-cząsteczkową) jest efektem zastosowania zasad dynamiki i prostych technik uśredniania do układu cząsteczek określonego w mikroskopowej definicji gazu doskonałego. Jest pierwotną i okrojona wersja mechaniki statystycznej. Pozwala łączyć kinematyczne wielkości dotyczące pojedynczych cząstek gazu z termodynamicznymi parametrami takimi jak ciśnienie czy temperatura. Rozwinęli ją m.in. R.Boyle, D.Bernoulli, R.Clausius i C.Maxwell.

Ciśnienie gazu według teorii kinetycznej

Gaz - zgodnie z przyjętym modelem - to zespół wielu cząsteczek - punktów materialnych poruszających się chaotycznie. Cząsteczki te zderzają się ze sobą. Zderzają się też ze ściankami naczynia i te właśnie zderzenia są dla nas szczególnie interesujące. W trakcie zderzeń ze ściankami zmienia się wektor prędkości cząsteczek. Zgodnie z drugą zasadą dynamiki F = m (Dv/Dt) do zmiany prędkości ciała potrzebna jest siła. W tym przypadku jest to siła z jaką ścianka działa na cząsteczkę podczas zderzenia. A skoro ścianka działa na cząsteczki gazu, to, zgodnie z trzecia zasadą dynamiki, cząsteczki gazu oddziałują pewna siłą na ścianki. Widzimy wiec, że na poziomie mikroskopowym za ciśnienie gazu wywierane na ścianki naczynia odpowiedzialne jest oddziaływanie cząsteczek gazu ze ściankami podczas zderzeń.

Ścisła zależność jest następująca:

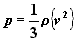
gdzie {v²} oznacza średnią w całym zespole wartość kwadratu prędkości cząstki a r jest gęstością gazu.

Inną popularne postacie tego wzoru otrzymujemy pamiętając, że np. r = masa/objętość , a z kolei masa gazu toM = nm/V ( m oznacza masę jednego mola gazu, a n to ilość moli).

pV = 1/3nm{v²}

Można teżzapisać masą jako M = N m - ilość cząsteczek pomnożoną przez masę cząsteczki.

Daje to:

pV = 1/3Nm{v²}

pV = 2/3N{E_k}

Oczywiście {E_k}= 1/2 m {v²} oznacza średnią wartość energii kinetycznej cząsteczek gazu.

Niekiedy mówi się też o tzw. średniej prędkości kwadratowej, określanej jako pierwiastek ze średniego kwadratu prędkości:

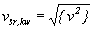
Jest ona większa od prędkości średniej, może być jednak używana do zgrubnego oszacowania średniej prędkości cząsteczek w gazie. Na podstawie podanego powyżej związku mamy

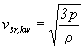
Kinetyczna interpretacja temperatury gazu

Znajomość wyprowadzonego powyżej wzoru na ciśnienie gazu pozwala na podanie kinetycznej interpretacji temperatury. Łącząc zależność
pV = 2/3 N {E_k} z równaniem Clapeyrona pV = NkT otrzymujemy

NkT = 2/3 N {E_k}

czyli

{E_k} = 3/2 k T

Widać więc że temperatura jest niczym innym jak miarą średniej energii kinetycznej cząsteczek gazu i że energia cząsteczek gazu zależy wyłącznie od temperatury.

Jest to podstawowy wynik kinetycznej teorii gazu doskonałego. Pamiętając, że {E_k}= 1/2 m {v²}, możemy z powyższego związku otrzymać "termiczną" postać wzoru na średnią prędkość kwadratową:

.

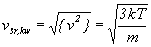Ten ciekawy rezultat wiąże wprost prędkość cząsteczek z temperaturą i masą. Dla gazu składającego się z cząsteczek o różnych masach, w danej temperaturze większe prędkości (oczywiście biorąc pod uwagę wartości średnie) będą miały cząsteczki o mniejszej masie. Tym właśnie tłumaczymy nieobecność wodoru w ziemskiej atmosferze. Cząsteczki wodoru, jako najmniej masywne, miały największe prędkości, w szczególności często większe od drugiej prędkości kosmicznej (prędkość ucieczki) co spowodowało ich odpływ w przestrzeń kosmiczną.

Różnicowanie prędkości w zależności od masy jest też podstawą rozdzielania izotopów. Cząsteczki zawierające lżejsze jądra szybciej dyfundują. Wielokrotnie powtarzany proces dyfuzji przez porowate przegrody prowadzi do wyselekcjonowania cząstek różniących się masą. Tak np. prowadzi się proces wzbogacania uranu.

Energia wewnętrzna i ciepło molowe - gaz jednoatomowy

Energią wewnętrzną nazywamy całkowitą energię związaną z chaotycznym ruchem cząsteczek ciała oraz z ich wzajemnymi oddziaływaniami. W przyjętym przez nas modelu (gaz doskonały) cząsteczki ze sobą nie oddziałują na odległość, nie ma żadnej energii potencjalnej związanej z ich wzajemnym oddziaływaniem, stąd cała wewnętrzna energia gazu sprowadza się do energii kinetycznej. Skoro (średnio rzecz biorąc) energia kinetyczna jednej cząsteczki równa jest E_k = 3/2 kT, to dla całego zespołu N cząsteczek mamy

U = N Ek = 3/2 NkT = 3/2 nRT

Jak widać - energia wewnętrzna gazu doskonałego jest zależna wyłącznie od temperatury gazu i do niej proporcjonalna.

Porównując z: U = nC_vT łatwo otrzymamy wzór określający ciepło molowe gazu w stałej objętości

C_v = 3/2 R

C_p = C_v + R = 5/2 R

k = C_p/C_v = 5/3

Zasada ekwipartycji energii

Wynik E = 3/2 kT otrzymany dla gazu jednoatomowego nie opisuje poprawnie gazu o bardziej złożonych cząsteczkach. W przypadku gazu składającego się z cząsteczek rozumianych jako nie związane ze sobą punkty materialne jedyna możliwa do pomyślenia energia to energia kinetyczna ruchu postępowego. Rozszerzając nieco nasz model możemy wyobrazić sobie budulec gazu nie jako punkty, lecz dwu lub wieloatomowe cząsteczki. Takie cząsteczki mogą wykonywać również obroty, a atomy w cząsteczkach mogą wykonywać oscylacje wokół położenia równowagi.Każdą z tych możliwości (liczymy tylko niezależne od siebie) - nazywamy stopniem swobody. Dla cząsteczki rozumianej jako punktu materialnego mamy trzy niezależne możliwe ruchy - trzy stopnie swobody. Są to ruchy postępowe wzdłuż trzech prostopadłych osi. Każdy z tych ruchów może wykonywać cząsteczka niezależnie od pozostałych.

Zasada ekwipartycji energii głosi, że w wielocząsteczkowym zespole, jakim jest gaz średnia energia przypadająca na każdy stopień swobody jest taka sama.

Skoro, jak obliczyliśmy, na trzy stopnie swobody cząsteczki punktowej przypada łącznie E = 3/2kT, to łatwo zauważyć, że energia przypadającą na jeden stopie swobody równa jest:

E_{st sw} = 1/2 kT

Energia wewnętrzna i ciepło molowe - gaz wieloatomowy

W świetle tego co zostało powiedziano wyżej energia cząsteczki gazu o i stopniach swobody jest równa

E = i E_{st sw} = i/2 kT ,

a energia wewnętrzna gazu złożonego z N cząsteczek gazu o i stopniach swobody jest równa

U = N i E_{st sw}.

U = i/2 NkT = i/2nRT

Ciepła molowe i wykładnik adiabaty wynoszą więc odpowiednio

C_v = i/2 R

C_p = C_v + R = (i+2)/2 R

k = C_p/C_v = (i+2)/i

Wystarczy teraz przeliczyć stopnie swobody różnych cząsteczek. Dla gazu jednoatomowego mamy i = 3 (trzy niezależne ruchy postępowe) a co za tym idzie C_v = 1/2 R, C_p = 3/2 R, k = C_p/C_v = 3/2 =1,67.

Dla gazu o cząsteczce dwuatomowej i = 5 (trzy ruchy postępowe i dwa obroty wokół osi prostopadłych do osi cząsteczki), co daje C_v = 5/2 R,
C_p = 7/2 R, k = C_p/C_v = 7/5 = 1,40.

Dla pozostałych gazów o bardziej złożonych cząsteczkach i = 6 (trzy ruchy postępowe i trzy obroty) i C_v = 3 R, C_p = 4 R,
k = C_p/C_v = 4/3 = 1,33.

W rzeczywistości obraz jest bardziej złożony. Kolejne stopnie swobody (w tym oscylacje) włączają się wraz ze wzrostem temperatury i w różnych przedziałach temperatur ciepła molowe przybierają różną wartość.