 Teoria
względności dla humanistów
Teoria
względności dla humanistów
UWAGA!
Tekst ten jest bardzo obszerny. Polecam ściągnięcie
dokumentu w wersji .pdf  ściągnij ściągnij
Spis
treści
Wstęp
|
Układy odniesienia |
Zasada względności |
Prędkość światła |
Doświadczenie Michelsona-Morleya | Transformacje
| Zdarzenie
| Dylatacja
czasu | Skrócenie
długości | Jednoczesność
zdarzeń | Czas
i przestrzeń są względne | Paradoks
bliżniąt | Inne
Teoria
względności Einsteina jest jednym z najciekawszych
zjawisk współczesnej nauki i cywilizacji. Prawie każdy
o niej słyszał, wzór E = mc2 jest najsłynniejszym
wzorem fizyki w ogóle, a w świadomości przeciętnego
zjadacza wyrobów piekarniczych teoria ta zbliża się
w równym stopniu do prawdziwej wiedzy, jak do magii
i metafizyki. Jednak, mimo tak wielkiej popularności
medialnej teorii Einsteina, rzadkością są osoby które
znają jej podstawy Dlaczego? - zapewne większość ludzi
nie wierzy, aby kiedykolwiek mogli zrozumieć teorię
względności. Słynna jest przecież anegdota o pytaniu
skierowanym do Einsteina: „czy to prawda, że
tylko dwie osoby na świecie rozumieją teorię względności?”
– ten miał odpowiedzieć – „a kto
jest tym drugim?...”.
Teoria Einsteina składa się z dwóch części: szczególnej
teorii względności i napisanej parę lat później
ogólnej teorii względności. I o ile ta druga
teoria jest rzeczywiście bardzo trudna matematycznie,
to szczególną teorię względności jest w stanie opanować
w miarę zdolny uczeń ogólniaka. Prawdą jest też, że
sam Einstein musiał uznać sprawność innych uczonych
w posługiwaniu się jego aparatem matematycznym jego
teorii (a wielu przypadkach nawet wyższość), ponieważ
okazało się, że wynikające z ogólnej teorii względności
modele kosmologiczne zostały niezależnie rozwinięte
w sposób, który zadziwił samego twórcę.
Na
czym polega „względność”?
Ttermin
ten odnosi się do sytuacji gdy to samo zjawisko jest
obserwowane z dwóch (przynajmniej dwóch, bo może i
więcej) różnych pozycji, miejsc, punktów widzenia (w fizyce mówimy o dwóch różnych „układach
odniesienia”) i gdy powstaje problem uzgodnienia
jak te punkty widzenia do siebie się odnoszą. Coś
jest względne, gdy przy zmianie punktu odniesienia,
zmienia się także sposób widzenia zdarzeń, sytuacji.
Np.
fakt słabych wyników ucznia w szkole inaczej wygląda
z punktu widzenia nauczyciela, inaczej ucznia, a jeszcze
inaczej rodzica. Czyli: sam fakt problemów w nauce
jest niezmienny, ale widzenie tego faktu jest
dość często różne - względne.
Powstaje
zatem zasadniczy problem: jak uzgodnić ze sobą
różne punkty widzenia (w fizyce obserwacje prowadzone
w dwóch układach odniesienia)? Lub w innym ujęciu
można by problem postawić tak: jaką procedurę zastosować,
aby poznać i porównać punkt widzenia drugiej strony?
Owo
uzgadnianie poglądów pomiędzy ma w istocie dwie warstwy,
które dość mylą się części osób:
| |
pierwsza
to warstwa prawdy i fałszu, pomyłek, przeoczeń
i błędnych interpretacji |
| |
druga
to obiektywna względność odniesień –
tutaj nie mówimy już o pomyłkach, czy celowym
zakłamaniu sprawy. Po prostu – często
jest tak, że po zmianie układu odniesienia rzeczy
w sposób naturalny i prawdziwy zaczynają być
inne. |
Układ
odniesienia jest podstawowym pojęciem związanym z
teorią względności. Wszystkie rozważania tej teorii
wiążą się z podstawowym pytaniem:
Jak
ten sam zestaw zdarzeń jest opisywany w różnych
układach odniesienia?
Mówiąc
inaczej - jak dokonać transformacji współrzędnych
przestrzennych i czasowych zdarzeń.
W
fizyce przyjmowana jest zasada (będąca jednym z założeń
teorii względności, ale nie tylko jej), że:
Nie
ma wyróżnionych układów odniesienia.
Co
to oznacza? – wyobraźmy sobie, że jest sobie
obszar w kosmosie, w którym latają sobie bezładnie
atomy pierwiastków promieniotwórczych. Ta chmura uranu,
radu, i innych atomów z jądrami gotowymi do rozpadu
nie jest związana z żadną gwiazdą, galaktyką ani układem
gwiazdowym – ot dryfuje sobie przez niezmierzone
otchłanie wszechświata. Co jakiś czas któreś z jąder
atomowych rozpada się - wypromieniowuje cząstkę alfa
i zamienia się w inny atom, zaś fakt, a z nim czas
i miejsce tego rozpadu jest rejestrowany przez obserwatorów
w wałęsających się tu i ówdzie rakietach (na rysunku
są dwie takie rakiety – A i B, prędkości rakiet
i cząstek są zaznaczone niebieskimi strzałkami).

Pilot
każdej z rakiet może zarejestrować ten sam rozpad
inaczej – po pierwsze w innej odległości od
rakiety, atom mógł też poruszać się z różną prędkością
względem każdej z rakiet.
Powstaje
pytanie:
pilot której rakiety widzi ten świat rozpadów promieniotwórczych
bardziej „prawdziwie”?
- ten z rakiety zielonej, czy z niebieskiej?
-
myślę, że jeśli ktoś nie ma jakichś bardzo sprecyzowanych
preferencji kolorystycznych, to nie znajdzie argumentu
przemawiającego na za wyróżnieniem którejś z rakiet,
czy któregoś z pilotów. Dlatego uznajmy jako fakt
- pilot każdej rakiety obserwuje otoczenie ze swojego
układu odniesienia jednakowo „prawdziwie”,
choć każdy inaczej.
A
to jest właśnie niezależność od układu odniesienia - żadna z rakiet nie jest w swoim opisie rzeczywistości
faworyzowana ani dyskryminowana. Oczywiście nie tylko
rakiety nie są wyróżniane, bo tak samo dobry będzie
opis sytuacji w chmurze radioaktywnej sporządzony
przez mieszkańca Ziemi, ufoludka z Marsa, czy przewodniczącego
związku planet w układzie Syriusza. Po prostu każdy
ma jednakowe „prawo” aby ten świat widzieć
po swojemu. Jednocześnie żaden z nich nie ma prawa
narzucać swojego układu odniesienia innym –
zakładamy, że prawidłowo wykonane w jakimś układzie
pomiary są w tym układzie prawdziwe.
Podobną
sytuację względności mamy dla dwóch obserwatorów patrzących
na samochód wiozących młodą parę. Balonik przyczepiony
do samochodu nowożeńców najczęściej w czasie jazdy
drga i podskakuje jak szalony. Jednak inaczej widzi
tę sytuację przechodzień, a inaczej kierowca samochodu.
Dla przechodnia balonik drga i jedzie, a dla
kierowcy balonik tylko drga. I prawda obu obserwatorów
jest obiektywna (w tym sensie, że nikt
nie popełnia błędu) – bo rzeczywiście z zewnątrz
patrząc to balonik przesuwa się, a ze środka patrząc
– nie. Czyli chociaż opisy obu obserwatorów
różnią się, to obaj mają rację – ruch
jest względny.
Tutaj
warto wspomnieć o psychologicznej cesze większości
ludzi – otóż mamy wrodzoną skłonność uznawać,
że to co „było od dawna” i co jest „duże”
jest bardziej prawdziwe. Gdy myślimy o „prawdziwym”
kapuśniaku to zapewne takim jaki robiła mama i babcia,
gdy się zastanawiamy kto ma rację, jako argument pada,
że tak „wszyscy” uważają (wszyscy, czyli
„dużo” ludzi). I mało kto zastanowi się,
że kilkaset lat temu „wszyscy” mieli całkowicie
inne poglądy na wiele spraw, a za lat sto jacyś inni
„wszyscy” też będą myśleli odmiennie.
Podobnie, gdy myślimy o prędkości lecącej muchy, to
oczywiście mimowolnie będziemy odnosić ją do podłoża,
czyli wielkiej Ziemi, a nie do innej, poruszającej
się obok, muchy, czy jadącego rowerzysty. Podświadomie
uważamy, że prędkość muchy oceniana względem Ziemi
jest „prawdziwa” a względem innej muchy
– już nie. „Coś” duże, stabilne
w naszym umyśle staje się w sposób naturalny poziomem
odniesienia (naturalny oznacza tu jednak także „mimowolny”,
„niezauważalny”).
W
odróżnieniu od psychologii, fizyka jest bardziej „sprawiedliwa”
– zakłada, że faworyzowanie wielkich układów
odniesienia nie ma podstaw. Trzeba sporej pracy umysłowej
aby uwolnić się od dominacji dużych i stałych obiektów
i zacząć swobodnie obserwować świat z dowolnie wybranego
poziomu.
Jak
napisano w części o układach odniesienia, wiele rzeczy
w różnych układach odniesienia jest różnych, wiele
wielkości będzie miało wartości zależne od tego z
poziomu jakiego układu są mierzone. Pojawia się istotne
pytanie: Czy wszystko jest względne? Czy dowolne elementy
sytuacji mogą być różne? Odpowiedź na nie daje m.in.
Einsteinowska zasada względności.
Postuluje ona, że:
Dowolne
prawo przyrody ma jednakową postać we wszystkich inercjalnych
układach odniesienia.
Uczniom
szkoły, chciałbym też przy okazji przypomnieć,
że odwołaliśmy się przed chwilą do pierwszej zasady
dynamiki Newtona, która głosi, że gdy nie ma działania
siły zewnętrznej, wtedy ciała poruszają się ze
stałą prędkością (może przyda się na sprawdzianie).
Jak
rozumieć zasadę względności?
Ustaliliśmy
wcześniej, że te same zdarzenia mogą w różnych układach
odniesienia być inaczej widziane. Jednak, czy w związku
z tym zmieniać się mogą również prawa fizyki?
Odpowiedź Einsteina brzmi: NIE. Liczby w równaniach
fizyki będą różne, ale ostatecznie równanie musi być
zachowane. Nie ma zatem takiego układu odniesienia,
w którym przestaje obowiązywać prawo grawitacji, lub
w którym siła z tego prawa wynikająca nagle staje
się zależna nie od kwadratu lecz od sześcianu odległości
(jednak wartość tej siły i same odległości mogą się
w różnych układach odniesienia różnić).
Zatem, wbrew naiwnym poglądom, Einstein nie twierdził,
że „wszystko” jest względne. Faktem jest
natomiast, że zjawiska obserwowane z różnych układów
odniesienia mogą być różnie opisywane.
Czym
jest światło?
Współczesna fizyka nie wyjaśnia jeszcze wielu elementów
fenomenu światła - co prawda wiemy, że ma ono dwoistą
naturę: korpuskularno - falową, wiemy też, że przenosi
najważniejsze (z punktu widzenia naszego obrazu świata)
oddziaływanie - oddziaływanie elektromagnetyczne i
wiemy, że prędkość światła w próżni jest bardzo ważną
ważną stałą fizyczną. Jednak wciąż dla badaczy światło
jest obiektem zagadkowym.
Światło
jako nośnik informacji
Z
punktu widzenia teorii względności światło jest istotne
jeszcze z jednego powodu, nie wynikającego bezpośrednio
z fizycznych właściwości. Jest nim fakt, że światło
(a bardziej ogólnie - fala elektromagnetyczna) jest
nośnikiem informacji.
Dla
zwykłych ludzi (nawet nie fizyków) informacyjna rola
światła jest dość oczywista. Przecież najczęściej
właśnie za pomocą tego medium dowiadujemy się o zajściu
określonych zdarzeń, jako że normalny, zdrowy człowiek
większość informacji o świecie czerpie właśnie za
pomocą narządu wzroku.
Jednak w odniesieniu do teorii względności fakt przenoszenia
informacji za pomocą światła ma znaczenie o wiele
bardziej fundamentalne - stał się on podstawą dla
nowej wizji czasu i przestrzeni. Można powiedzieć,
że światło poprzez swój fakt przenoszenia informacji
niejako "stwarza przestrzeń i czas".
W rozważaniach relatywistycznych umiejscowienie przestrzenne
jakiegoś obiektu poznajemy po czasie w jakim dociera
od tego obiektu światło (a stąd możemy łatwo obliczyć
drogę jaką przebył sygnał).
x
wysłania sygnału = x odbioru
sygnału + droga jaką przebył sygnał
Podobnie czas zajścia zdarzenia wysłania sygnału świetlnego
jest rejestrowany jak czas odbioru sygnału pomniejszony
o czas lotu tegoż sygnału do odbiornika.
t
wysłania sygnału = t odbioru
sygnału - t lotu sygnału
Większość wniosków szczególnej teorii względności
została wyprowadzona ze stosunkowo prostych przeliczeń
czasu lotu sygnałów świetlnych.
Dodatkową
okolicznością, która w ogromnym stopniu zaważyła na
powstaniu teorii względności było odkrycie przez fizyków
amerykańskich - Michelsona i Morleya - bardzo niezwykłego
faktu związanego z rozchodzeniem się światła. Okazało
się bowiem, że ruch światła przeczy dość fundamentalnemu
prawu fizyki klasycznej - prawu dodawania prędkości.
Klasyczne
prawo dodawania prędkości
W
naszym normalnym świecie obowiązuje tzw. klasyczne
prawo dodawania prędkości. Np. jeżeli Staś jedzie
na rowerze z prędkością 8 m/s, a goni go Jaś z prędkością
12 m/s, to prędkość Jasia względem Stasia wynosi 4
m/s.
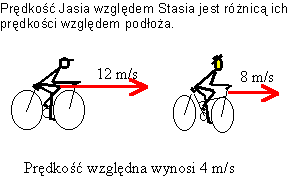
W
przypadku gdyby Jaś jechał naprzeciw Stasia, to ich
względna prędkość byłaby sumą prędkości względem podłoża
i wynosiłaby 20 m/s. Z tą prędkością Jaś zbliża się
do Stasia, a Staś do Jasia.
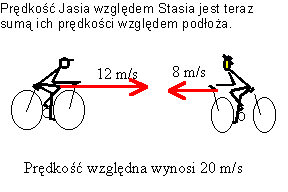
Podobna
sytuacja miałaby miejsce, gdyby Jaś próbował dogonić
muchę poruszającą się z prędkością 15 m/s:
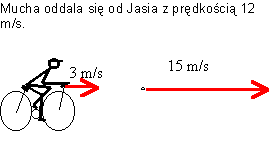
W
przypadku gdy mucha zbliża się do Jasia prędkość względna
wyniesie 18 m/s:

A
co klasyczne prawo dodawania prędkości ma wspólnego
ze światłem?
-
Otóż okazuje się, że światło nie podlega, opisanemu
wyżej, klasycznemu prawu dodawania prędkości. Tak
jest i już – stwierdzono to doświadczalnie (patrz
dalej Doświadczenie Michelsona - Morleya).
W
słynnym doświadczeniu wykonanym przez fizyków amerykańskich
– przez Michelsona i Morleya - próbowano sprawdzić
prędkość rozchodzenia się światła w układzie związanym
z Ziemią.
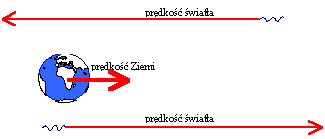
Jak
to wynika z klasycznego prawa dodawania prędkości,
ponieważ nasza planeta okrąża Słońce z prędkością
30 km/s, to powinien dać się zauważyć efekt zmiany
prędkości światła względem Ziemi w sytuacjach gdy:
| |
światło
porusza się zgodnie z ruchem Ziemi |
| |
światło
porusza się przeciwnie do ruchu Ziemi |
Światło,
"puszczone" ze źródła w eter (bo przyjmowano,
że światło rozchodzi się w hipotetycznym ośrodku zwanym
"eterem") powinno poruszać się wolniej,
gdy Ziemia zawierająca odbiornik porusza się zgodnie
z ruchem eteru (prędkości się odejmują), a szybciej,
gdy porusza się przeciwnie (prędkości się dodają).
Można powiedzieć, że analogiem muchy z przykładu z
Jasiem jest teraz światło, rowerzystą - Ziemia.
Powstawał jednak pewien problem do rozstrzygnięcia
– w którą stronę porusza się eter?
- czy „wieje” w którąś stronę, czy jest
nieruchomy względem Słońca (a może względem Galaktyki)?
Pierwotnie
pomyślane doświadczenie zaprojektowane przez Michelsona
(odbyło się w roku 1881) miało właśnie wykryć ów ruch
eteru - jako różnicę w odbieranej prędkości światła
(powinna się ona zmieniać dla dla różnych kierunków
ruchu Ziemi i różnych kierunków ustawień układu doświadczalnego).
W sześć lat później doświadczenie zostało powtórzone
przez Michelsona wspólnie z Morleyem.
W każdym przypadku jego wynik był jednak absolutnie
zaskakujący – bez względu na kierunek ruchu
Ziemi, porę dnia i roku, kierunek ustawienia ramion
interferometru - odczyty wykazywały na to samo –
że prędkość światła względem Ziemi ma zawsze niezmienioną
wartość.
Prowadziło
to do absurdalnego (z punktu widzenia mechaniki klasycznej)
wniosku, że
Wykrywana
prędkość światła względem Ziemi jest niezależna od
tego, czy jest skierowana zgodnie, czy przeciwnie
względem prędkości naszej planety.
Ale
ponieważ doświadczanie było wielokrotnie powtarzane
w różnych warunkach i
- czy to poruszając się naprzeciw światłu,
- czy zgodnie z kierunkiem jego prędkości
więc nie pozostawało nic innego jak z pokorą przyjąć
jego wynik.
Czyli stwierdzić fakt, że prędkość światła dla każdego
układu odniesienia ma dokładnie tę samą wartość:
c = 299792458 m/s – w przybliżeniu 300 tys.
km/s.
Mówiąc obrazowo, żebyśmy nie wiem jak szybko „gonili”
światło, to ono i tak będzie oddalało się od nas z
tą samą prędkością i żebyśmy nie wiem jak chcieli
go przyspieszyć poprzez zbliżanie się do niego, to
ono i tak będzie względem nas poruszało się z prędkością c.
Dzięki temu doświadczeniu okazało się dodatkowo, że
koncepcja eteru jest pozbawiona podstaw fizycznych
– eteru nie ma, a światło nie rozchodzi się
"w czymś", tylko po prostu "względem
układu odniesienia".
Prędkości
światła nie da się przekroczyć
Z
doświadczenia Michelsona Morleya wypływa także kolejny
ważny wniosek (jeden z postulatów teorii względności
Einsteina):
Prędkość
światła jest największą możliwą prędkością względną
między dwoma obiektami.
Lub
inaczej:
Nie ma na świecie obiektu, który by się mógł oddalać
od obserwatora szybciej niż światło.
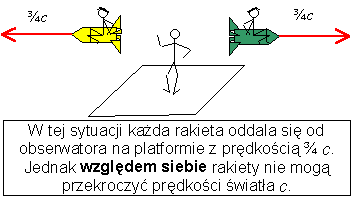
No
dobrze... – ktoś powie – ale wyobraźmy
sobie taką sytuację: Jedna rakieta porusza się z prędkością
¾ c w prawo, a druga z prędkością ¾
c w lewo. To przecież jedna od drugiej oddala
się z prędkością 1,5 c...
Otóż
nie. Prędkość względna jednej rakiety wobec drugiej
jest mniejsza niż c, bo ruch obiektu
materialnego nie może odbywać się z prędkością większą
niż prędkość światła.

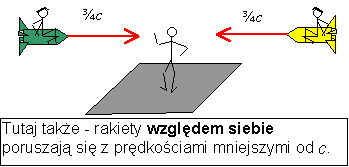
A
więc np.
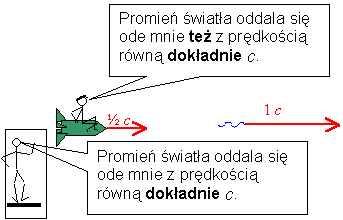
Jeśli skądś wysłano promień światła, a następnie w
ślad za tym promieniem wyśle się obserwatora poruszającego
się z prędkością równą połowie prędkości światła,
to i tak względem obserwatora prędkość promienia będzie
ciągle równa c.
Jak
to jest możliwe?
- Obserwator w układzie poruszającym się inaczej
mierzy czas i inaczej mierzy odległość
między tymi samymi zdarzeniami (np. pomiędzy
momentem osiągnięcia przez światło początku i końca
określonego odcinka). I jak podzieli on swoją drogę
dla światła przez swój czas dla światła,
to z tych liczb wyjdzie dla światła zawsze prędkość
równa c, bez względu na to z jaką prędkością
porusza się obserwator.
Transformacje,
czyli uniwersalny tłumacz dla zjawisk w różnych układach
odniesienia
W
sytuacji gdy mamy dwa układy odniesienia pojawia się
problem (a z postawienia tego problemu wynika właśnie
teoria względności):
Jak odnieść wyniki pomiarów wykonane w jednym układzie
do analogicznych pomiarów wykonanych w drugim?
Transformacje
w fizyce
W
fizyce analogiczna sytuacja jest zazwyczaj prostsza,
bo istnieje aparat matematyczny, który po podstawieniu
liczb do odpowiednich równań pozwala na ścisłe ustalenie
co zmierzy obserwator w innym układzie odniesienia.
Ten układ równań tłumaczący świat jednego obserwatora,
na świat innego, nazywany jest transformacją.
Dla układów inercjalnych (przypominam jeszcze raz
– układów, które same nie poruszają się z przyspieszeniem)
rozważane są zazwyczaj dwie transformacje:
Transformacja
Galileusza – opisuje świat na sposób tradycyjny,
czyli przed wprowadzeniem TW. W transformacji Galileusza
(zgodnej z mechaniką niutonowską) czas i przestrzeń
są traktowane jako jednolite, niezmienne, niezależne
od układu odniesienia. Tutaj czas jaki upływa między
dwoma zdarzeniami jest niezależny od tego z poziomu
jakiego układu odniesienia jest wyznaczany - powinien
mieć tę samą wartość dla obserwatora spoczywającego,
poruszającego się z ogromną prędkością, czy znajdującego
się w silnym polu grawitacyjnym. Podobnie jest z odległością
między dwoma punktami - jeśli w jednym układzie odległość
ta wynosi x metrów, to tyle samo metrów odległość
ta powinna mieć w dowolnym innym układzie odniesienia.
Transformacja
Lorentza (Hendrik Lorentz opracował wzory tej
transformacji; później skorzystał z nich Albert Einstein)
– ujmuje zjawisko szerzej, z uwzględnieniem
efektów relatywistycznych. Z tej to transformacji
można wyprowadzić większość „bulwersujących”
efektów teorii względności.
Zdarzenie
- pojęcie podstawowe dla rozważań związanych z
teorią względności
Podstawowym
pojęciem obu transformacji jest zdarzenie.
Jest to o tyle novum, że transformacje zrezygnowały
do pewnego stopnia z posługiwaniem się pojęciem obiektu.
Zdarzenie tym różni się od obiektu, że jest dokładnie
określone w przestrzeni i w czasie. Konkretnie
– każde zdarzenie dzieje się w jednej chwili
i w jednym punkcie w przestrzeni. Takie podejście
oszczędza zbędnych dywagacji na temat rozmiarów obiektu
i czasu jego istnienia. Właściwie można powiedzieć,
że zdarzenie reprezentuje jeden punkt czasoprzestrzenny.
Natomiast obiekt jest najczęściej dość nieokreślony
pod jakimś względem - po pierwsze ma zazwyczaj rozmiary,
a poruszając się różne części obiektu w różnych momentach
osiągają ten sam punkt przestrzeni. Dlatego wygodniej
jest widzieć świat teorii względności przez pryzmat
zdarzeń, a nie obiektów świata materii.
Opisywanie
świata za pomocą zdarzeń uświadamia nam jeszcze jeden
ważny element naszego widzenia rzeczywistości –
wszystko co do nas dociera jest związane z jakimś
zdarzeniem, jakąś przemianą. Mówiąc konkretnie
- gdyby tuż obok naszego ucha przeleciał obiekt o
masie większej niż słońce, ale nic by z tego nie wynikło
– nie powstałoby światło, ani pole sił mogące
nas o tym poinformować, a dodatkowo nie zmieniłby
się żaden element otoczenia, to dla nas i tak sytuacja
byłaby dokładnie taka, jakby nic nie przeleciało.
Właściwie, to bez względu na to, co się wokół nas
rzeczywiście dzieje, my mamy dostęp wyłącznie do tych
rzeczy, które się nam objawią przez jakieś wykrywalne
zdarzenia.
Ale
wróćmy od rozważań zmierzających w kierunku filozofii,
do samych transformacji Galileusza i Lorentza...
Dla małych prędkości układów odniesienia (małych w
porównaniu z prędkością światła wynoszącą ok. 300
tys. km/s) wyniki produkowane przez obie transformacje
są prawie takie same (dla zwykłych życiowych prędkości
różnica jest mniejsza niż miliardowe części procenta).
Różnica jaka pojawia się pomiędzy przewidywaniami
transformacji Galileusza i transformacji Lorentza
ujawnia się dopiero dla prędkości porównywalnych z
prędkością światła. Wtedy to ujawniają się następujące
zadziwiające efekty transformacji Lorentza:
wydłużenie
czasu
skrócenie długości
Wszystkie
efekty transformacji Lorentza wynikają z faktu niezależności
prędkości światła od układu odniesienia, będącej wnioskiem
z doświadczenia Michelsona - Morleya. Bo skoro suma
dwóch prędkości różnych od zera daje w efekcie jedną
z tych prędkości, to oznacza, że powinniśmy zrewidować
nasze wyobrażenia na temat podstawowych składników
pojęcia prędkości (przypominam, że prędkość obliczamy
dzieląc drogę przez czas) - drogi (przestrzeni) i
czasu.
Wszystko
wynika z transformacji
W
dalszych rozważaniach przedstawione zostały wnioski
wynikające z teorii względności. Wszystkie one wynikają
z faktu dokonania transformacji (w tym wypadku transformacji
Lorentza) określonych zdarzeń z jednego układu odniesienia
do drugiego (najczęściej z układu spoczywającego,
do układu w ruchu). Okazuje się np., że tak zadziwiający
efekt wolniejszego upływu czasu w układach poruszających
(patrz rozdział o dylatacji czasu) wynika tylko z
tego, że czas taki jest inaczej "widoczny",
gdy jest obserwowany w ruchu. Podobnie jest z pozostałymi
zjawiskami teorii względności.
Po
podstawieniu do równania transformacyjnego danych
dla zdarzeń obserwowanych z poruszającego się układu
odniesienia, okazuje się że te same zjawiska są
widziane tak, jak by zachodziły wolniej. Mówimy więc
o wydłużeniu czasu w układach poruszających
się. Np. jeśli będziemy obserwować zegarek umieszczony
w rakiecie poruszającej się z dużą prędkością, to
stwierdzimy, że zegarek ten spóźnia się względem identycznego,
znajdującego się na naszym ręku. Zjawisko to nie wynika
w żaden z sposób z wady zegarka, czy błędów odczytu
– tak po prostu jest, że widziany w obiekcie
poruszającym się czas płynie wolniej. Chcę tu
zwrócić uwagę na stwierdzenie „widziany w poruszającym
się obiekcie” – należy to rozumieć w ten
sposób, że jeśli my "zaglądamy" do obszaru
znajdującego się w ruchu, to zachodzące tam zdarzenia
zachodzą dla nas wolniej, niż obserwowane bezpośrednio
w tym układzie. Dla obserwatora w środku poruszającego
się układu wszystko jest, tak jak było wcześniej –
czyli zegarek chodzi zgodnie z jego normalnymi konstrukcyjnymi
możliwościami.

Uzasadnienie zjawiska wydłużenia czasu jest w rozdziale...
Czy
zaobserwowano gdzieś zjawisko wydłużenia czasu?
Zjawisko
wolniejszego upływu czasu w układach poruszających
się jest powszechnie obserwowane przez fizyków badających
cząstki elementarne w akceleratorach. Większość
tego typu cząstek rozpada się samorzutnie po pewnym
czasie. Jednak cząstki poruszające się z dużymi prędkościami
mają wyraźnie dłuższy czas życia. I wartość tego wydłużenia
jest zgodna z wzorami relatywistycznymi.
Zjawisko
dylatacji czasu zaobserwowano też bardziej bezpośrednio.
Super dokładne zegary atomowe wysłane w jednej z rakiet
spóźniały się dokładnie w takim stopniu jak przewiduje
to teoria względności.
Słowo
„zrozumieć” oznacza najczęściej wytworzenie
sobie w umyśle określonego obrazu, który ilustruje
mechanizm działania jakiegoś prawa. Rzeczywistość
akademicka nie przejmuje się tym wyobrażeniem rozumienia
– fizycy, gdy chcą coś wykazać, wyciągają kredę
a następnie maczkiem zapisują kilkanaście stron tekstu
matematycznego najeżonego całkami, logarytmami i innymi
atrakcjami z analitycznego piekła rodem. Z kolei dla
mnie (a chyba nie tylko dla mnie) najlepszym sposobem
pokazania czegoś jest przekonanie delikwenta bez wzorów
– najlepiej za pomocą prostych słów i gestów,
a w fizyce – paru narysowanych obrazków. Powyższą
metodę tłumaczenia umownie określam jako „metodę
machania rękami”.
Niniejszym więc, na przykładzie prostych rozważań
geometrycznych, postaram się wyjaśnić dlaczego z pewnych
prostych założeń wynika, że czas w układzie poruszającym
się musi płynąć wolniej oraz, że długości ulegają
skróceniu w kierunku ruchu.
Zastanówmy
się jak w istocie mierzymy czas. Przypomnienie sobie
zasad działania większości zegarów pokazuje, że najczęściej
pomiar ten jest oparty o jakieś jednostajnie zachodzące
zjawisko. Pierwszymi zegarami były klepsydry przesypujące
piasek lub przelewającymi wodę, później wahadła, a
dopiero ostatnio owym ruchomym medium stały się drgania
elektryczne w zegarkach kwarcowych.
My,
bardziej tradycyjnie, posłużymy się klepsydrą. Jednak
będzie to klepsydra unowocześniona – klepsydra
świetlna, w której elementem „ruchomym”
jest światło.

Wyobraźmy
sobie, że mamy dwa idealnie odbijające zwierciadła,
które uwięziły promień światła odbijający się między
nimi. Dzięki prostopadłemu zwierciadeł względem ruchu
promienia, będziemy mogli mierzyć czas – narasta
on wraz z ilością odbić promienia świetlnego, czyli
„odwróceń” naszej klepsydry. Np. jeśli
odległość między zwierciadłami wynosi 3 m, to czas
upływający pomiędzy odbiciami wynosi jedną setną mikrosekundy
(prędkość światła to 300 tys. km/s, a więc na przebycie
trzech metrów światło potrzebuje właśnie jedną stumilionową
sekundy). Mierząc ilość odbić światła od zwierciadeł
będziemy mogli precyzyjnie ustalić upływ czasu - np.
tysiąc odbić, będzie wyznaczało czas 1/100 s, a milion
odbić, to już 10 s.
Zaletą
tego zegara jest zastosowanie światła, którego prędkość
jest stała we wszystkich układach odniesienia. Dlatego
łatwo będzie nam porównywać wskazania tego zegara
dla różnych obserwatorów.
Klepsydra
w ruchu
Zastanówmy
się teraz jakie będą wskazania naszej klepsydry świetlnej,
jeśli będziemy obserwować ją w ruchu. Zegar ustawimy
prostopadle do kierunku ruchu, aby nie przeszkadzało
nam dodatkowo ew. skrócenie długości jakie występuje
dla ustawienia zgodnego prędkością.
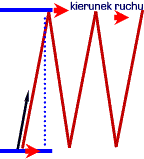
Z
rysunku widać, że światło obserwowane w ruchu przebywa
nie tylko drogę prostopadle do drogi pomiędzy zwierciadłami,
ale uzyskuje także składową wzdłuż kierunku ruchu.
Obrazowo mówiąc: bieg promieni rozciąga nam się jak
harmonia, ponieważ kolejne punkty, które odwiedza
światło przesuwają się dla obserwatora ruchomego.
Dlatego ostatecznie musi ono przebyć nieco dłuższą
drogę niż dla zegara spoczywającego – przecież
teraz porusza się po przekątnej prostokąta w którym
zawiera się obraz jednego odbicia promienia. Ale przebycie
dłuższej drogi przy tej samej prędkości (przypominam,
że wartość prędkości światła jest stała we wszystkich
układach odniesienia), oznacza dłuższy czas
jej przebywania. Dlatego czas pomiędzy poszczególnymi
odbiciami promienia jest dłuższy w układzie poruszającym
się niż spoczywającym.
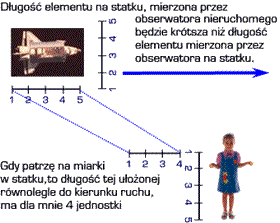
Podobnym
zjawiskiem do wydłużenia czasu jest skrócenie długości.
Oznacza ono, że miarka o długości 1 metra obserwowana
wtedy gdy koło nas przelatuje, jest dla nas krótsza,
niż gdyby leżała sobie spokojnie obok. Efekt ten zachodzi
jednak tylko w kierunku ruchu – gdyby
miarka metrowa z naszego przykładu była ustawiona
prostopadle do prędkości, to zarówno w układzie w
którym spoczywa, jak i w tym w którym się porusza
– cały czas będzie miała dokładnie 1 metr. Wynika
z tego np. że przelatująca kula zamienia się dla obserwatora
widzącego ją w ruchu w elipsoidę.
Czy
skrócenie długości zaobserwowano doświadczalnie?
Przeprowadzenie
doświadczenia potwierdzającego fakt skrócenia długości
w układach poruszających się jest niezwykle trudne.
Mierzenie długości obiektów w ruchu musi odbywać się
w oparciu o precyzyjne pomiary odbitych sygnałów świetlnych,
a więc i tak nie stanowiłoby prostego, bezpośredniego
potwierdzenia. Jak do tej pory nie są znane fizycznie
zrealizowane doświadczenia potwierdzające lorentzowskie
skrócenie długości. Zjawisko to jest jednak na tyle
silnie związane z innymi efektami teorii względności
(a w większości przypadków są one bardzo dobrze potwierdzone
doświadczalnie), że świat nauki nie poddaje faktu
skrócenia długości w wątpliwość.
Skrócenie
długości - wytłumaczenie
Skrócenie
długości w pewnym stopniu częściowo wynika z
faktu spowolnienia czasu. Jeśli gdzieś odległość między
punktami będziemy mierzyć czasem lotu promienia świetlnego,
to krótszy czas lotu, w innym układzie odniesienia,
automatycznie będzie odpowiadał mniejszej odległości.
Jednak
dlaczego skrócenie długości występuje tylko dla kierunku
zgodnego z kierunkiem ruchu? – przecież światło
rozchodzi się z jednakową prędkością w każdą stronę...
Czyżby czas miał „kierunek” i był inny
dla promieni równoległych, a inny dla prostopadłych
względem prędkości obiektu?
Wyjaśnienie tych problemów nie jest proste, dlatego
postaram się przedstawić bardziej "porządne"
rozumowanie, oparte o rozważania geometryczne. Wytłumaczenie
to jest nieco skomplikowane, a chociaż nie operuje
wzorami i wymagane umiejętności matematyczne sprowadzają
się do zrozumienia zasady dodawania długości odcinków,
to trzeba trochę nad nim "przysiąść".
Kto się nie boi – niech czyta następujący niżej
rozdział.
Precyzyjne okazanie zjawiska skrócenia długości w
układzie poruszającym się jest bardziej skomplikowane,
niż to ma miejsce w przypadku dylatacji czasu.
Najpierw
ustalmy na czym polega pomiar długości. Sprawa
jest o tyle skomplikowana, że dla bardzo szybko poruszających
się obiektów nie sposób jest przyłożyć miarki aby
odczytać ile dany odcinek ma metrów, czy centymetrów.
Trzeba więc posłużyć się inną metodą. Einstein zaproponował
tu wykorzystanie światła (wciąż to światło...). Jeżeli
obiekt spoczywa, to po prostu wyznaczamy czasy w jakich
promień świetlny leci do nas od jednego i drugiego
końca odcinka. Gdy odcinek się porusza, to złapanie
promienia nie jest też takie proste – przecież
cały czas początek i koniec mierzonego odcinka zmieniają
położenie i nie bardzo wiadomo, które punkty ze sobą
porównywać.
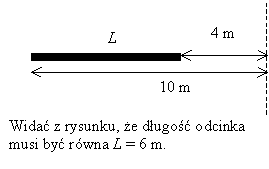
Zajmijmy
się jednak najpierw tym prostszym przypadkiem. Wiadomo
jeśli w linii prostej do początku odcinka jest 4m,
a do końca 10m to długość odcinka będzie równa 6m.
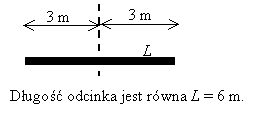
Można
też wyznaczać odległości od końców odcinka mierząc
odległości od środka odcinka:
W
przypadku odcinka w ruchu, wyznaczanie odległości
jest trudniejsze, bo zarówno początek, jak i koniec
odcinka bez przerwy się nam przesuwają. Dlatego niezwykle
ważne jest, aby przypilnować tego, że położenia początku
i końca trzeba wyznaczyć w tym samym czasie. Bo odległość
między poruszającymi się punktami, wyznaczana w różnych
momentach nie da nam na pewno dobrej długości odcinka.
Aby
więc zagwarantować, określanie końców odcinka w tym
samym czasie proponuję użycie następującej metody:
| |
Do
końców mierzonego odcinka przyczepimy zwierciadła. |
| |
Do
tych zwierciadeł będziemy wysyłać promienie
świetlne. Mierząc czas, po którym odbity promień
wróci, będziemy mogli wyznaczyć odległość
zwierciadła w momencie odbicia |
| |
Promienie
świetlne będziemy wysyłać gdzieś z punktu
położonego między zwierciadłami - tam będzie
źródło sygnału radarowego sprzężone z detektorem,
czyli z odbiornikiem promieni. Detektor będzie
oczywiście wyposażony w zegar umożliwiający
określenie czas lotu promieni świetlnych.
|
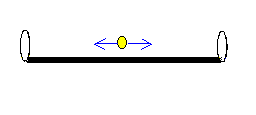
| |
Aby
zagwarantować, że odbicie od obu końców zajdzie
jednocześnie, można postąpić tak: co
niewielki ułamek sekundy wysyłane są promienie
świetlne w obie strony. Każdy wysłany promień
światła różni się minimalnie kolorem od poprzedniego.
Później, gdy będziemy analizować światło odbite
weźmiemy pod uwagę tylko te promienie, które
wrócą jednocześnie i będą miały ten
sam kolor (aby nie było sytuacji, w której
od odebraliśmy jeden promień odbity od zwierciadła
wcześniej, a drugi później, co jest możliwe
gdyby punkty odbicia były w różnych odległościach
od detektora). Zmierzony czas, po którym wysłane
promienie wrócą po odbiciu będzie miernikiem
długości odcinka – ponieważ każdy promień
pokonuje swoją połówkę odcinka 2 razy to znaczy,
że wystarczy wymnożyć czas lotu dowolnego
z dwóch promieni przez prędkość światła, aby
dostać szukaną długość odcinka. |
Wyobraźmy
sobie teraz, że nasz długość naszego odcinka będzie
mierzona w dwóch różnych układach odniesienia:
| |
Pierwszy
układ odniesienia, to układ na sztywno związany
z odcinkiem. Odcinek w nim spoczywa. |
| |
Drugi
układ odniesienia jest w ruchu względem
odcinka, czy (co na to samo wychodzi) odcinek
jest w ruchu względem niego |
Uwaga:
na tym, i następnych rysunkach, mierniczego związanego
z układem spoczywającym względem odcinka będę oznaczał
kolorem zielonym, a mierniczego obserwującego odcinek
w ruchu – niebieskim.
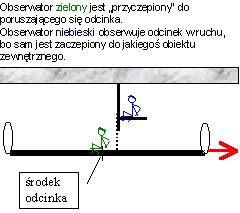
Rozważmy
teraz jak będzie zachodził pomiar długości w tych
układach odniesienia.
1
układ, w którym odcinek spoczywa (zielony)
Tutaj
sytuacja jest bardzo prosta – skoro nasz miernik
odległości cały czas znajduje się dokładnie w środku
odcinka, to promienie odbite będą miały identyczną
drogę do przebycia i będą wracały jednocześnie.
Czas
powrotu wysłanych promieni pomnożony przez prędkość
światła da nam długość odcinka. Nie ma znaczenia,
w którym momencie te promienie będą wysłane –
byle tylko zawsze startowały ze środka odcinka - i
tak wszystkie wysłane promienie tego samego koloru
będą wracać jednocześnie.
Oczywiście
inaczej byłoby, gdyby nasz miernik znajdował się nie
w środku odcinka, dlatego można powiedzieć, że fakt
jednoczesnego przyjścia promieni odbitych jest jednocześnie
wskaźnikiem ustawienia detektora w środku.
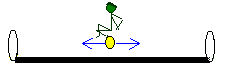
2.
pomiar odległości odcinka poruszającego się (dla obserwatora
niebieskiego)
Tutaj
sytuacja jest znacznie bardziej skomplikowana.
Dla obserwatora próbującego zmierzyć odcinek w ruchu,
zwierciadła odbijające cały czas zmieniają swoje położenie.
Przypadkowo wysłane promienie świetlne zapewne odbiją
się od zwierciadeł w różnym czasie i dlatego nie dadzą
nam informacji o długości odcinka.
Np.
gdybyśmy próbowali dokonać pomiaru wysyłając promień
w chwili, gdy mija nas dokładnie środek odcinka, to
jedno zwierciadło (na rysunku lewe) zdążyłoby się
do momentu odbicia nieco przybliżyć do detektora (na
rysunku o odcinek b). Drugie zwierciadło (prawe)
miałoby za to czas, aby się oddalić. W efekcie promienie
odbite nie wróciłyby jednocześnie do detektora, a
my mielibyśmy odczyty położeń zwierciadeł dokonane
w różnym czasie.
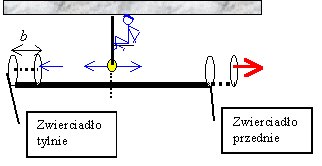
Dlatego
aby zagwarantować, że odbicia od zwierciadeł będą
następować w tym samym czasie, musimy zacząć
wysyłać impulsy świetlne szybko jeden po drugim.
Jeśli zaczniemy tak robić zaraz po tym jak detektor
minie pierwszy koniec odcinka, to najpierw będą przychodzić
impulsy odbite właśnie od przedniego zwierciadła (które
oddala się od detektora), a dopiero po znacznie dłuższym
czasie od zwierciadła tylnego. Jednak wraz z przesuwaniem
się zwierciadeł czasy przylotu promieni będą się stawać
coraz bliższe sobie – pierwsze zwierciadło będzie
się od detektora oddalać, a drugie przybliżać. W pewnym
momencie jeden z tych czasów spełni nasz warunek jednoczesnego przyjścia obu wysłanych promieni (zakładamy, że impulsy
świetlne są wysyłane rzeczywiście bardzo często jeden
po drugim) – i o ten właśnie przypadek nam chodzi.
Zauważmy, że ów interesujący nas promień odbija się
od obu zwierciadeł dokładnie w momencie, w którym
środek odcinka mija obserwatora.
Następne
impulsy będą oczywiście przychodziły rozsynchronizowane,
bo przednie zwierciadło oddali się już dalej niż tylnie.
Zastanówmy
się teraz nad sytuacją w dojdzie do naszego właściwego
pomiaru – tzn. gdy promienie wysłane do obu
zwierciadeł jednocześnie wrócą do detektora.
Wysłanie owego kluczowego impulsu powinno nastąpić
nieco przed momentem, w którym środek odcinka
wraz z mierniczym zielonym mija detektor niebieski.
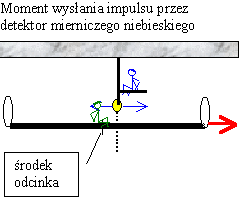
Dzięki
temu, podczas lotu promienia zwierciadła przesunie
się na tyle, że samo odbicie od nich nastąpi dokładnie
w chwili, gdy środek odcinka i oba detektory znajdą
się tym samym punkcie.
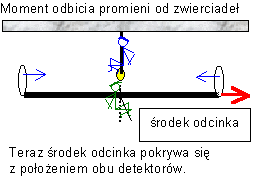
W
tym samym momencie, gdy promienie będą jednocześnie
odbijane od zwierciadeł, oba detektory znajdują się
w jednym punkcie. Wtedy impulsy trafią parami jednocześnie
do detektora, a czas ich lotu będzie miarą długości
odcinka.
Powiązanie
ze sobą pomiarów zachodzących w obu układach
Teraz
najtrudniejszy moment – musimy powiązać ze
sobą odczyty czasów lotu promieni (a więc i długości
odcinków) następujące w układzie, w którym odcinek
porusza się (niebieskim) i w układzie względem odcinka
nieruchomym (zielonym).
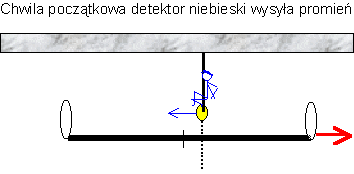
W
tym celu przyjrzyjmy się co dzieje się z impulsem
świetlnym wysłanym przez detektor niebieski. W czasie
lotu do zwierciadła tylnego, w pewnym momencie, mija
on środek odcinka (a więc także znajdujący się tam
detektor zielony).
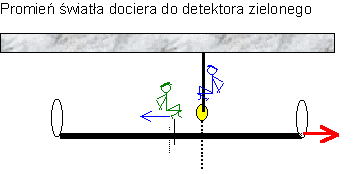
Zwróćmy
uwagę na jedną rzecz: lecący promień od detektora
niebieskiego może służyć mierniczemu zielonemu „jak
własny” – wystarczy tylko, że w momencie
mijania go omawianego promienia dodatkowo wyśle bliźniaczy
promień w przeciwnym kierunku do zwierciadła przedniego.
Wtedy całość będzie mógł uznać także za swój pomiar
długości. Tak więc od momentu minięcia środka odcinka
przez lecący promień, pomiar czasu (a zatem i odległości)
będzie dla obu mierniczych wspólny.
Cóż
się dalej więc z owym wspólnym pomiarem dzieje?
| |
najpierw
impuls świetlny dolatuje do zwierciadła
i oczywiście natychmiast odbija się od
tegoż zwierciadła (w momencie odbicia pokrywają
się ze sobą środek odcinka i położenie obu
detektorów – tego mierzącego długość
odcinka w ruchu i tego spoczywającego) |
| |
impuls
leci z powrotem. W tym czasie detektor
obserwatora zielonego związanego ze środkiem
odcinka przesuwa się już za detektor mierniczego
niebieskiego. |
| |
impuls
dociera z powrotem do detektora, z którego
został wysłany (niebieskiego) – pomiar
obserwatora patrzącego na odcinek z zewnętrz
zostaje tu zakończony – tutaj więc kończy
się wspólna część lotu promieni.
Jednak do tej chwili środek odcinka wraz z
detektorem zielonym przesunął się na odległość
od detektora niebieskiego równą tej, w której
znajdował się podczas startu impulsu (tyko
teraz jest po przeciwnej stronie). Załóżmy
więc, że detektor niebieski nie pochłonie
całej wiązki światła (np. jest ona szeroka),
jej część przelatuje swobodnie obok zmierza
teraz do detektora zielonego, aby zostać tam
zarejestrowana. |
Na
koniec impuls dociera do zielonego detektora.
Pojawia
się teraz pytanie zasadnicze:
Który
z naszych dwóch mierniczych (zielony, czy niebieski)
zarejestrował dłuższy czas przelotu sygnału mierniczego?
A
może nie było różnicy, między tymi czasami?
Jasne
jest, że dłuższy czas odpowiada dłuższej przebytej
drodze, a zatem zarejestrowaniu większej wartości
długości odcinka.
Aby
odpowiedzieć sobie na to pytanie. Trzeba prześledzić
lot promieni bardzo dokładnie, bo istnieje
dość subtelna różnica między zmierzonymi czasami przelotu.
Porównajmy
jednak najpierw główne czasy przelotu promieni. W
tym celu podzielimy wszystkie etapy ruchu na rozłączne
odcinki (patrz rysunek). Aby wyjaśnienia były czytelne
drogę promienia jest rozbita na dwa rysunki. Kolejność
następujących zdarzeń wynika z numeracji opisów –
od 1 do 7.

Teraz
promień świetlny udaje się w drogę powrotną
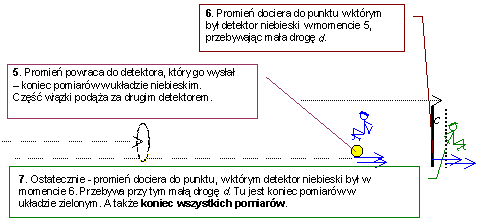
Zastanowimy
się teraz dla którego z układów promień mierniczy
przebył dłuższą drogę.
Najpierw
rozpiszemy drogę dla układu niebieskiego. Składa się
ona z odcinków:
1
– 2, 2 – 3, 3 – 4, 4 – 5.
Teraz
droga dla układu zielonego. Właściwe odcinki to:
2
– 3, 3 – 4, 4 – 5, 5 – 6,
6 – 7.
Widać
od razu, że odcinki: 2 – 3, 3 – 4, 4 –
5 pokrywają się. Różnica zawiera się w odcinkach:
1
– 2: występujący tylko dla układu niebieskiego.
5
– 6, 6 – 7: występujące tylko dla układu
zielonego.
Myślę,
że uważny czytelnik zauważy, że odcinek 1 –
2 jest krótszy od sumy odcinków 5 – 6 i 6 –
7. Mało tego - jest on nawet krótszy od samego odcinka
5 – 6, i to o długość d. Ponieważ zaś
dochodzi do tej różnicy jeszcze jedna wartość d (bo tyle wynosi długość odcinka 6 – 7), więc
widzimy, że:
droga
promienia w układzie zielonym jest dłuższa od drogi
w układzie niebieskim o 2d.
A
to oznacza, że:
Czas pomiaru odległości w układzie zielonym jest większy
niż w układzie niebieskim.
A
ponieważ czas świadczy o długości odcinka, więc możemy
powiedzieć:
W
układzie niebieskim zmierzona długość odcinka jest
krótsza!
Uogólniając:
Obserwator mierzący długość odcinka będącego w ruchu
uzyska rezultat mniejszy niż obserwator względem
tego odcinka spoczywający.
A
to jest właśnie owo sławetne relatywistyczne skrócenie
długości
Innym
ciekawym zjawiskiem TW (ale chyba już nie paradoksem)
jest problem jednoczesności zdarzeń. Przykład,
który tu opiszę pochodzi od samego Einsteina, więc
postaram się nie zmieniać w nim zbyt wiele.
Wyobraźmy
sobie superekspresowy pociąg przejeżdżający przez
stację (pociąg Einsteina). Pociąg jest o tyle nietypowy,
że porusza się z prędkością bliską prędkości światła.
Poza tym pociąg ma tylko jeden wagon, na którego obu
końcach znajdują się drzwi otwierane fotokomórką.
W środku wagonu znajduje się lampka, która wysyła
światło otwierające drzwi. Zastanówmy się nad tym
jak będą otwierały się drzwi pociągu z punktu widzenia
osoby znajdującej się wewnątrz pociągu, a jak dla
zawiadowcy stacji.

Łatwo
jest wszystko przewidzieć dla osoby wewnątrz pociągu
– ponieważ prędkość światła jest stała, więc
rozchodzące się promienie świetlne odbędą taką samą
drogę do jednych i drugich drzwi wagonu, dlatego fotokomórki
zadziałają jednocześnie i drzwi otworzą się jednocześnie.
Z
punktu widzenia zawiadowcy stacji sytuacja jest bardziej
skomplikowana. Cóż on widzi: w pewnym momencie w środku
przejeżdżającego wagonu rozbłysło światło. Jego promienie
poruszające się względem zawiadowcy z prędkością światła
(prędkość ta jest niezależna od układu odniesienia
– patrz doświadczenie Michelsona Morleya), zachowują
się jednak różnie – promień wysłany w przód
goni drzwi z fotokomórką i ostatecznie, zanim je dopędzi,
przebędzie znacznie dłuższą drogę, niż promień poruszający
się kierunku tyłu pociągu, który zmierza na spotkanie
swoich drzwi. W efekcie najpierw otworzą się drzwi
tylne, a dopiero potem przednie.
Jak
z tego widać zdarzenia równoczesne w jednym układzie
odniesienia mogą być nie równoczesne w innym układzie.
Mówiąc inaczej – nie ma jednolitego zegara we
wszechświecie, który tak samo odmierza czas dla wszystkich
zdarzeń i wszystkich układów odniesienia.
I
jeszcze jedna uwaga: zachwianie jednoczesności zdarzeń
przy zmianie układu odniesienia może wystąpić tylko
wtedy, gdy zdarzenia odbywają się w różnych miejscach.
Im bardziej oddalone od siebie w przestrzeni są jakieś
zdarzenia, tym bardziej mogą być one rozdzielone czasowo
w różnych układach odniesienia. Jednak zdarzenia zachodzące
w tym samym miejscu i czasie nigdy nie będą mogły
być rozdzielone.
Niezależność
prędkości światła od układu odniesienia nie da
się wytłumaczyć w oparciu o tradycyjne poglądy
na temat czasu przestrzeni. Skoro prędkość, wyliczana
jako iloraz drogi przez czas, osiąga wartość z innych
powodów absurdalną, to jedynymi możliwościami są:
| |
albo
trzeba zmienić zasady matematyki |
| |
albo
trzeba zmienić poglądy na temat przestrzeni |
| |
albo
trzeba zmienić poglądy na temat czasu. |
Ostatecznie
okazało się, że nie trzeba aż uciekać się do drastycznej
reformy zasad matematyki i logiki, a wystarczy zmienić
nasze wyobrażenia dotyczące czasu i przestrzeni.
Czas
i przestrzeń, czyli czasoprzestrzeń
Aby
w zgodzie z fizyką wyobrażać sobie zależności czasoprzestrzenne,
należałoby zmodyfikować typowe podejście do tego tematu.
- po pierwsze i najważniejsze – musimy pożegnać
się z koncepcją czasu absolutnego i przestrzeni absolutnej.
Inaczej
mówiąc trzeba się pogodzić z faktem, że nie ma takiego
uniwersalnego zegara, który tyka jednakowo dla wszystkich
obiektów wszechświata. W zamian za to, każdy obiekt
(precyzyjniej byłoby powiedzieć „każdy układ
odniesienia”, ale na szczęście i tak układ odniesienia
możemy związać z obiektem, a łatwiej się myśli o czymś
co jest materialne) nosi swój własny prywatny czas,
którym "mierzy" wszystko co jest w stanie
zaobserwować. Jednak ten prywatny czas (tzw. czas
własny) i związane z nim prywatne "widzenie"
przestrzeni niekoniecznie da się zsynchronizować z
czasem przestrzenią innego obiektu.
Podobnie jak z czasem, jest z przestrzenią –
próżnia nie jest taką niewidzialną siatką, w której
każde miejsce jest z góry określone dla dowolnego
mierniczego ja odwiedzającego. W zamian za to, każdy
obiekt „nosi ze sobą” własną przestrzeń,
do której wedle aktualnej potrzeby „przyczepia”
otaczające go obiekty. I często okazuje się, że odległości
w przestrzeni jednego obiektu nie będą pokrywać się
z odległościami innego obiektu. Jednym stwierdzeniem
można to podsumować, że teraz:
Czas
i przestrzeń są względne.
Ponieważ
zaś przestrzeń wpływa na sposób rejestracji czasu,
a czas wpływa na widzenie przestrzeni, to uznano,
że dobrze jest posługiwać się pojęciem czasoprzestrzeni.
Pojęcie to staje się szczególnie użyteczne w ogólnej
teorii względności, gdy rozważane się zjawiska
zakrzywienia czasoprzestrzeni, a więc grawitacji.
Zjawisko
wydłużania się czasu obserwowanego w obiekcie poruszającym
się prowadzi do ciekawych problemów interpretacyjnych.
Najbardziej znanym jest paradoks bliźniąt.
Wyobraźmy
sobie, że dwóch braci bliźniaków urodziło się w epoce
lotów kosmicznych. Jeden z nich był mniej zaradny
i został nauczycielem, więc klepał przez całe życie
biedę w jakiejś szkole użerając się z coraz bardziej
niesforną młodzieżą. Drugi brat w czasie rozwoju płodowego
był położony bliżej źródeł pokarmu i w związku z tym
lepiej się rozwijał pod wieloma względami, a ostatecznie
urodził rzutki, dynamiczny, przebojowy. Dzięki tym
cechom charakteru dostał się do programu lotów kosmicznych
i poleciał na oddaloną o 10 lat świetlnych gwiazdę.
Posiedział tam z roczek (może dwa) i wrócił z powrotem
na Ziemię, gdzie został owacyjnie powitany przez społeczeństwo
świata.
Teraz
do opowieści należy dołączyć wiedzę wynikającą z teorii
względności. Ponieważ brat kosmonauta poruszał się
z prędkościami bliskimi prędkości światła, to oczywiście
jego czas płynął wolniej niż czas brata na Ziemi (patrz
dylatacja czasu). W efekcie po powrocie okazuje się,
że choć brat nauczyciel jest 70 letnim staruszkiem
z trudem dorabiającym do kiepskiej emerytury, to kosmonauta
wysiada z rakiety młody (jakieś 40 lat) i pełen werwy.
Bo skoro czas w jego układzie płynął wolniej, to on
musi być młodszy.

Świetnie!
– mamy już paradoks – niby są bliźniacy,
a jak się nierówno zestarzeli! – wykrzyknie
typowy czytelnik czasopism kobiecych, sportowych i
motoryzacyjnych.
A
ja na to:
Hola! – to jeszcze nie paradoks, to dopiero
efekt przewidziany przez teorię względności.
Paradoks
zacznie się dopiero wtedy, gdy uświadomimy sobie,
że przenosząc nasz układ odniesienia do rakiety (a przecież mówiliśmy, że żaden układ odniesienia
nie jest wyróżniony), to brat nauczyciel leci sobie
przez wszechświat oddalając się od rakiety na wielkim
pojeździe kosmicznym zwanym Ziemia. I z tego punktu
widzenia patrząc, to właśnie on powinien zestarzeć
się wolniej! – przynajmniej dla brata w rakiecie.
Kto więc będzie na końcu stary, a kto młody –
kosmonauta, czy nauczyciel?
Bo
przecież nie ma wyróżnionych układów odniesienia
i wśród bliźniaków też powinno być równouprawnienie.
Może to więc jednak nauczyciel jest młodszy od brata
kosmonauty? Paradoks wreszcie jest, bo absolutnie
nie widać powodu dla którego tylko jeden z braci miałby
okazać się lepszym w tym wyścigu po młodość.
Jak
uczą w podręcznikach, rozwiązanie paradoksu bliźniąt
istnieje tylko w oparciu o ogólną teorię względności.
Bo okazuje się, że istnieje istotna różnica
między oboma braćmi, która powoduje, że układ odniesienia
brata w rakiecie jednak jest wyróżniony. Brat,
który pozostaje na Ziemi nie podlega działaniu silnych
przyspieszeń, a brat kosmonauta musi się najpierw
rozpędzić, potem lecieć długo ruchem jednostajnym,
a potem znowu zahamować (u celu podróży). Podczas
powrotu sytuacja się powtarza, bo znowu mamy sekwencję:
rozpędzanie, lot, hamowanie. Ponieważ zaś przyspieszenia
rakiety powodują, że układ z nią związany staje się
układem nieinercjalnym, to szczególna teoria
względności się do tego przypadku nie stosuje. Po
odwołaniu się do ogólnej teorii względności,
która zajmuje się sytuacjami zachodzącymi także w
układach nieinercjalnych - paradoks znika.
I
jak głosi gminna wieść wśród fizyków, ta różnica układów
odniesienia powoduje, że brat kosmonauta rzeczywiście
będzie młodszy.
Zjawiska
einsteinowskiego świata
Relatywistyczne
wydłużenie czasu (nazywane też „dylatacją”
czasu) i skrócenie długości (określane przez fizyków
jako skrócenie Lorentza) nie są jedynymi „dziwnymi”
efektami zachodzącymi przy prędkościach bliskich prędkości
światła. Jest to dość zrozumiałe, bo skoro podstawy
postrzegania zjawisk – czas i przestrzeń ulegają
modyfikacji, to wszystko co od nich zależy, też będzie
się transformować inaczej, niż byśmy to sobie początkowo
wyobrażali. Dlatego zmienić trzeba m.in.:
Klasyczne
prawo dodawania prędkości – okazuje
się, że dwa obiekty poruszające się naprzeciw siebie
z prędkościami bliskimi prędkości światła, nie dają
prędkości zbliżania się (obserwowanej w jednym z tych
układów) większej niż prędkość światła.
Transformacja
przyspieszenia – ponieważ prędkość ulega
modyfikacji w układach szybko poruszających się, to
i przyspieszenie z tej prędkości wynikające, zachowywać
się będzie w nowy sposób.
Transformacja
energii i pędu – tu dochodzimy do słynnego
wzoru E = mc2. Jego konsekwencje wykraczają
daleko poza dywagacje u kogo zegarek się późni, a
u kogo nie. W oparciu o to proste równanie można wyjaśnić
tak fantastyczne efekty jak: istnienie antymaterii,
wybuchy jądrowe, produkcję energii w gwiazdach, a
nawet powstawanie wszechświata.
Spojrzenie
na grawitację. Zjawiska które do tej pory omawiałem
wynikają z tak zwanej „szczególnej teorii
względności”, czyli ograniczonego przypadku
teorii względności zajmującego się wyłącznie układami
inercjalnymi. „Ogólna teoria względności”
rozszerza naszą możliwość tłumaczenia zjawisk o układy
nieinercjalne, a co za tym idzie także o zjawiska
w polu grawitacyjnym. Ogólna teoria względności jest
bardzo trudna matematycznie ponieważ posługuje się
m.in. pojęciem tensora – obiektu zawierającego
w sobie wiele danych na raz (w OTW rozpatruje się
m.in. tensory o 256 składowych). Dlatego teoria ta
jest dostępna jedynie dla prawdziwych matematycznych
„twardzieli”.
Szczególna
teoria względności
Szczególna
teoria względności przewiduje między innymi następujące
efekty nieznane w fizyce klasycznej:
| |
Dylatacja
(wydłużenie) czasu obserwowanego z układu odniesienia
będącego w ruchu |
| |
Skrócenie
długości obserwowanej z układu odniesienia będącego
w ruchu |
| |
Zachwianie
równoczesności zdarzeń |
| |
Równoważność
masy i energii |
| |
Nowe
wzoru opisujące większość wielkości fizycznych
w inercjalnych układach odniesienia. Te wielkości
to m.in.: odległość, prędkość, przyspieszenie,
pęd, energia. |
Ogólna
teoria względności
Jednak
pełniejszą wiedzę o zjawiskach relatywistycznych daje
stworzona przez Einsteina nieco później ogólna
teoria względności. Teoria obejmuje:
To
samo co w szczególnej teorii względności plus dodatkowo:
Wyjaśnienie
pochodzenia zjawiska grawitacji
przewiduje efekt spowolnienia upływu czasu w silnym
polu grawitacyjnym
Stworzenie mechanizmu opisującego ewolucję wszechświata
(w szczególności rozszerzanie się wszechświata)
Problem
jest o tyle złożony, że w nauce słowo „teoria
prawdziwa” dawno już zatraciło sens znany przeciętnym
zjadaczom chleba. Bo „prawdziwość” najczęściej
oceniamy (poniekąd słusznie) po tym, czy dana rzecz
poprawnie zintegruje się z naszym umysłem. Dlatego
np. teoria bardzo dobra, ale przez nikogo nie zrozumiana
nie ma szansy na zaistnienie w nauce.
Teoria
powinna być zgodna z doświadczeniem.
Dlatego
powstaje oczywiste pytanie: czy takie zjawiska jak
wydłużenie czasu w układzie poruszającym się dadzą
się doświadczalnie sprawdzić?
Odpowiedź
brzmi: ależ tak, oczywiście! – przeprowadzono
wiele doświadczeń, z których jednoznacznie wynika,
że czas zachowuje się zgodnie z przewidywaniami Einsteina.
Najbardziej
typowymi są doświadczenia na cząstkach elementarnych.
Cząstki te są najczęściej obiektami o bardzo krótkim
czasie istnienia – zazwyczaj po ułamku sekundy
rozpadają się na inne cząstki, co daje się zaobserwować
w laboratoriach. Robiono więc doświadczenia na miuonach – cząstkach o czasie życia rzędu mikrosekundy.
Badano więc grupę szybko poruszających się miuonów
(z prędkościami porównywalnymi do prędkości światła)
oraz miuonów specjalnie do celów doświadczenia spowolnionych.
I okazało się, że te szybkie rozpadały się po wyraźnie
dłuższym czasie. Innymi doświadczeniami związanymi
z względnością czasu było wysłanie na orbitę superdokładnych
zegarów atomowych. Okazało się, że rzeczywiście następują
odchylenia ich „chodu” od podobnych zegarów
zostawionych na Ziemi.
Wreszcie
słynny wzór E = mc2. Gdyby nie był prawdziwy,
to nigdy nie wybuchłaby bomba atomowa, nie działałyby
reaktory jądrowe, ani akceleratory. Setki urządzeń
wybudowanych za grube miliardy dolarów nie mogłoby
działać, bo są one zbudowane z uwzględnieniem tej
teorii. Czy można podejrzewać finansistów wykładających
grube miliardy dolarów na te cele, o kierowanie się
idealistycznymi przesłankami, a przynajmniej chęcią
bezinteresownego oszukiwania świata? Czy możliwe jest,
aby wyłożyliby oni pieniądze na coś, co nie przyniesie
efektu?...
Poza
tym większość efektów fizyki jądra atomowego, cząstek
elementarnych czy ogólnie fizyki kwantowej zakłada
prawdziwość tej teorii i na co dzień wykorzystuje
ją w swoich przewidywaniach. A ponieważ wszystkie
uznane aktualnie teorie muszą być (i są) potwierdzone
doświadczalnie, to gdyby nagle okazało się, że teoria
względności jest całkiem nieprawdziwa – oznaczałoby
to absolutną ruinę całej współczesnej fizyki i
chemii...
Czy
można obalić teorię względności?
Rraczej
nie ma sensu dyskutować nad „prawdziwością”
teorii względności w tym sensie, że np. ktoś przyjdzie
i udowodni, że jednak „e nie równa się em ce
kwadrat”. Bez tego wzoru fizyka nie potrafi
się dzisiaj obejść. Jednak w miarę stabilna pozycja
teorii względności w dzisiejszej fizyce wcale nie
oznacza, że na temat czasu, przestrzeni, energii i
masy zostało powiedziane ostatnie słowo. Teoria względności,
oprócz wielkich sukcesów, ma również swoje słabości:
| |
jest
w pewnym zakresie niezgodna z mechaniką kwantową |
| |
są
pewne doświadczenia które stawiają pod znakiem
zapytania postulat nieprzekraczalności prędkości
światła |
Tylko
problem tkwi w tym, że nie bardzo wiadomo jak ułożyć
teorię, aby wszystko się zgadzało. Póki co –
czekamy na kolejnego geniusza fizyki, który:
| |
połączy
fizykę kwantową z teorią względności |
| |
stworzy
jednolitą teorię oddziaływań elektrosłabych,
silnych i elektromagnetycznych |
| |
i
ogólnie wyjaśni czym właściwie jest ten zadziwiający
świat... |
Teoria
względności na to nie odpowiada. Jedynie komplikuje
sprawę w stosunku do tradycyjnych poglądów pokazując
czym czas nie jest. Wiemy zatem, że nie
jest to jakby jednolity strumień taktujący cały
wszechświat jednym niezmiennym rytmem. Czas jest zależny
od układu odniesienia.
Ciekawym
matematycznym aspektem czasu w matematycznym opisie
teorii względności jest fakt, że spośród czterech
zmiennych czasoprzestrzeni: x, y , z, t - czas,
jako jedyny, łączy się z pozostałymi zmiennymi za
pomocą jednostki urojonej i (w matematyce jednostka
urojona i równa jest pierwiastkowi z minus
jeden).
Np. wzór tzw. interwału czasoprzestrzennego
- czyli jakby odległości w czasoprzestrzeni:
(Δs2 = - (Δx)2 - (Δy)2 - (Δz)2- (icΔt)2
zawiera
jednostkę urojoną i, stojącą przy zmiennej
czasowej.
Oznacza to, że w czasoprzestrzeni – łączącej
w jedno przestrzeń i czas, ta ostatnia zmienna jest
wyróżniona i zachowuje się (matematycznie rzecz ujmując)
odmiennie od pozostałych.
Wzory
teorii względności dotyczące czasu pokazują, że wraz
ze zbliżaniem się prędkości obiektu do prędkości światła,
czas zaczyna płynąć coraz wolniej, a dla samej prędkości
światła czas musiałby stanąć w miejscu. Niektórzy
wyciągają stąd wniosek, że gdyby tak jednak przekroczyć
prędkość światła (jakimś specjalnym sposobem) to,
oznaczałoby to odwrócenie biegu czasu. Jednak jest
to jak na razie pomysł z obszaru fantastyki naukowej,
bo rozpędzenie najmniejszego obiektu materialnego
do prędkości światła wymagałoby użycia nieskończenie
wielkiej energii. A co tu mówić o przekroczeniu tej
prędkości?...
Jeszcze
jednym ciekawym elementem teorii względności dotyczącym
czasu (w tym przypadku już Ogólnej Teorii Względności)
jest powiązanie upływu czasu z obecnością materii.
Np. czarne dziury wytwarzające bardzo silne pole grawitacyjne
powodują zakrzywienie czasoprzestrzeni, co z kolei
dla obserwatora zewnętrznego daje efekt spowolnienia
czasu.
Wykraczając
poza teorię względności, też możemy znaleźć ślady
ciekawych koncepcji związanych z pojęciem czasu. Niektórzy
sugerują np., że w świecie cząstek elementarnych czas
płynie inaczej niż w naszym makroskopowym świecie.
Być może nawet w bardzo niewielkim obszarze czas mógłby
się cofać? A może dla obiektów rzeczywiście elementarnych
czas stoi w miejscu?
Istnieją
też poważne teorie fizyczne opisujące zjawiska za
pomocą większej ilości wymiarów czasoprzestrzennych,
niż znane z teorii względności cztery wymiary (czyli
trzy przestrzenne i jeden czasowy) - np. teoria
strun posługuje się 10-cioma lub 11-toma wymiarami.
Wzory
teorii względności
Oznaczenia
i symbole
Prędkość
światła: c = 299792458 m/s
Prędkość
obiektu względem układu odniesienia: v.
Czynnik
γ - czynnik Lorentza (występuje w wielu wzorach
teorii względności).
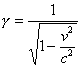
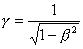
Wartości
γ :
| |
v = 0 → γ = 1 |
| |
v
< c → γ > 1 |
| |
v
= c → γ rośnie
do nieskończoności |
Czynnik
β - stosunek prędkości obiektu (obserwatora)
do prędkości światła:
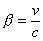
Dla
| |
v = 0 → β = 0 |
| |
v
< c → β <1 |
| |
v
= c → β = 1 |
Transformacja
Lorentza
Ustalenia
początkowe:
Rozpatrujemy
dwa inercjalne układy odniesienia – zwykły XYZ
i oznaczany ‘ (primem) X’Y’Z’.
Oba układy mają równolegle położone osie X Y Z. W
chwili początkowej środki obu układów pokrywają się
– czyli:
x
(t = 0) = x’(t’= 0) =
0
y
(t = 0) = y’(t’=
0) = 0
z
(t = 0) = z’(t’=
0) = 0
Prędkość
układu primowanego względem układu nieprimowanego
wynosi v i jest skierowana wzdłuż osi X-ów zgodnie
z jej zwrotem.
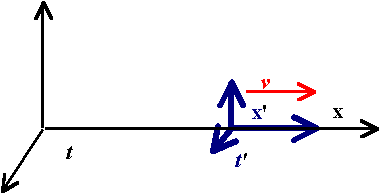
Wzory
transformacyjne
Oto
wartości poszczególnych współrzędnych dla zdarzenia
mającego w układzie nieprimowanym współrzędne: x,
y, z, t:
z'
= z
y'
= y
x' = γ ( x – vt )
t' = γ ( t – x β/c )
Wzory
transformacyjne - transformacja odwrotna:
z
= 'z
y
= y'
x = γ ( x’ + v t’ )
t
= γ ( t’ + x’ β/c )
Relatywistyczna
transformacja prędkości
Załóżmy,
że mamy cząstkę, której prędkość w układzie nieprimowanym
dana jest przez u. Prędkość względna układów wynosi
(jak w transformacji Lorentza) v.
u
= (ux, uy, uz)
W
układzie primowanym prędkość tej cząstki będzie widziana
jako:
u'
= (u’x, u’y,
u’z)
Przy
czym zachodzi:
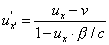
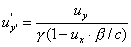
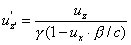
Przypadek
jednowymiarowy – dodawanie i odejmowanie prędkości
w jednym wymiarze
Aby
wzór łatwiej się oglądało pozbywamy się indeksu oznaczającego
współrzędną.
Wzór
na u’ w postaci rozpisanej:
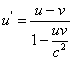
Co
można uznać za wzór na relatywistyczne odejmowanie
prędkości (czyli gdy obiekty, a zarazem układy odniesienia,
poruszają się w tym samym kierunku).
Wersja
dla obiektów/układów odniesienia poruszających się
w przeciwnych kierunkach (relatywistyczne dodawanie
prędkości ) będzie różnić się znakiem prędkości u.
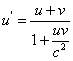
Wnioski
– po podstawieniu do wzorów otrzymamy:
dla
dowolnych u < c oraz v ≤
c zachodzi u’< c
dla
u = c i v = c, u’=c
Dylatacja
czasu
Oznaczmy
czas własny układu przez t0 - jest
to czas upływający pomiędzy dwoma zdarzeniami w układzie
w którym zdarzenia zachodzą w tym samym miejscu.
Czas t' mierzony pomiędzy tymi zdarzeniami
w układzie poruszającym się dany będzie wzorem
t'
= t0 /γ
Jest
to efekt tzw. dylatacji (wydłużenia czasu), ponieważ
γ ≥ 1, więc
t0 ≥ t'
Oznacza
to, że w układzie primowanym upływa mniej
minut, a więc czas się wydłuża.
Skrócenie
długości
Niech
długość pewnego odcinka w układzie, w którym spoczywającym
względem tego odcinka wynosi l0.
Długości tego odcinka obserwowane z układu ruchomego
skracają się γ krotnie.
lobserwowane_w_ruchu=l0/γ
ponieważ
γ ≥ 1, więc lobserwowane_w_ruchu
≤ l
Oznacza
to, że odcinek poruszający się wraz z obserwatorem
jest γ razy dłuższy
Zjawisko
powyższe nazywane jest niekiedy kontrakcją długości
lub skróceniem Lorentza – Fitzgerlada.
Interwał
czasoprzestrzenny
Np.
wzór tzw. interwału czasoprzestrzennego.
W
postaci symetrycznej względem wszystkich współrzędnych
Δs2 = - (Δx)2 – (Δy)2 – (Δz)2 - (icΔt)2.
Lub
prościej:
Δs2 = (cΔt)2 - (Δx)2 – (Δy)2 – (Δz)2 |