 PRAWO HUBBLE'A
PRAWO HUBBLE'A
Już w
1912 roku V. M. Slipher odkrył, że linie widmowe prawie
wszystkich galaktyk (za wyjątkiem kilku najbliższych)
przesunięte są w różnym stopniu w stronę długofalową
- ku czerwieni. Jednak dopiero w roku 1929 E. Hubble
badając skrupulatnie widma galaktyk o znanych już
wówczas odległościach (wyznaczonych różnymi metodami)
stwierdził istnienie liniowej korelacji pomiędzy przesunięciem
ku czerwieni linii widmowych a odległością do galaktyki.
Interpretując to przesunięcie widma jako efekt Dopplera
wysunął śmiałą hipotezę, że Wszechświat jako całość
ekspanduje i wszystkie odległości w nim rosną z czasem
a prędkość wzajemnego oddalania się spełnia zależność:
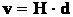 (1)
(1)
gdzie
d - odległość do galaktyki, zaś H - współczynnik proporcjonalności
nazwany później stałą Hubble'a. Jak zobaczymy poniżej,
określenie "stała" nie jest w ogólności
trafne, gdyż wielkość ta zmienia się w kosmologicznej
skali czasu. Lepiej jest więc używać nazwy - parametr
Hubble'a, zaś dla wartości tego parametru w obecnym
czasie to wprowadzono oznaczenie Ho
i dla niego termin "stała" jest już
w pełni adekwatny. Wielokrotnie weryfikowano obserwacyjnie
wartość stałej Hubble'a Ho i pomiary te
wciąż są powtarzane. Na ich podstawie przyjmuje się
obecnie wartość
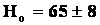 km/s/Mpc. km/s/Mpc.
Oznacza
to, ze z każdym megaparsekiem odległości prędkość
oddalania się obiektu od dowolnie wybranego punktu
początkowego narasta o ok. 65 km/s. Ponieważ występujące
w jednostkach stałej Hubble'a kilometry oraz megaparseki
można wyrazić w metrach więc, po uproszczeniu przez
metry, podstawową jednostką dla wielkości H jest [s-1]
czyli odwrotność czasu. Czas ten, czyli (Ho)-1
jest co do rzędu wielkości porównywalny z wiekiem
Wszechświata.
Odkrycie
Hubble'a stało się inspiracją do poszukiwania takich
modeli kosmologicznych, które zawierałyby w sobie
możliwość ekspansji. Omawiano je w rozdziale "kosmologiczne
rozwiązania równań Einsteina".
Funkcjonowanie
prawa Hubble'a możemy zademonstrować graficznie na
przykładzie modelu Wszechświata o geometrii typu sferycznego.
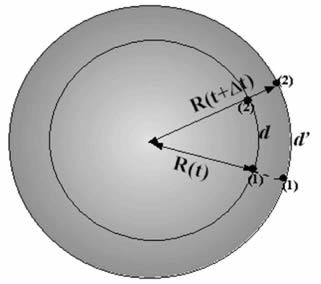
Niech naszą trójwymiarową przestrzeń reprezentuje
dwuwymiarowa powierzchnia sfery, na której wybieramy
dwa punkty - np. galaktyki (1) i (2) .Promień tej
sfery i jej środek nie należą już do naszej powierzchni
- są poza nią, a więc jakby poza tym modelowym wszechświatem.
Oznaczamy sobie przez R(t) promień sfery w chwili
t zaś przez R(t + Dt) promień po pewnym czasie Dt. Podobnie odległości pomiędzy
wybranymi punktami oznaczymy odpowiednio przez d oraz
d' . Jak widać, punkty symbolizujące galaktyki oddaliły
się od siebie nie na skutek ruchów własnych po powierzchni
lecz na skutek ekspansji samej sfery.
Możemy
więc napisać prostą proporcję :
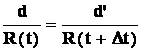 (2)
(2)
Stąd:
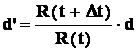 (3)
(3)
Zmiana
odległości pomiędzy punktami (1) i (2) będzie:
 (4)
(4)
Dzieląc
stronami przez przyrost czasu Dt dostaniemy prędkość oddalania się
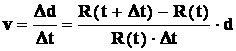 (5)
(5)
Rozpoznajemy
w tym wyrażeniu znany iloraz różnicowy (w granicy
pochodną). Możemy zrobić więc podstawienie:
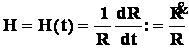 (6)
(6)
po którym
formuła (5) uzyskuje postać prawa Hubble'a v = H*d.
Widzimy więc jawnie, że parametr Hubble'a H jest zmienny
w czasie a tempo tej zmiany zależy od typu modelu
kosmologicznego. W rozdziale o rozwiązaniach kosmologicznych
pokazano, że np. dla modelu o geometrii euklidesowej
zależność H(t) jest
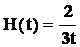 (7)
(7)
.Pomiary
Hubble'a z lat 20-tych dotyczyły galaktyk o odległościach
kilkadziesiąt (lub niewiele ponad 100) milionów parseków.
W tej sytuacji względnie dobry przybliżeniem było
stosowanie nierelatywistycznego wzoru Dopplera na
przesunięcie ku czerwieni:
 (8)
(8)
Gdy później
odkryto bardziej odległe galaktyki oraz kwazary o
bardzo dużych przesunięciach widm, koniecznym stało
się stosowanie relatywistycznego wzoru Dopplera:
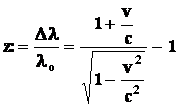 (9)
(9)
Jak widać
z niego, gdy 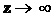 to v---> c. Obecnie najdalsze (i zarazem najstarsze)
zaobserwowane galaktyki i kwazary mają przesunięcia
ku czerwieni z>5. Za najstarszy obserwowany obiekt
we Wszechświecie można uznać reliktowe promieniowanie
tła, które w chwili termodynamicznego oderwania się
od materii miało temperaturę kilku tysięcy Kelvinów
obecnie zaś ma T=2.75 K. Odpowiadające tej zmianie
temperatury przesunięcie ku czerwieni termicznego
widma tego promieniowania daje wartość 'z' rzędu 103.
to v---> c. Obecnie najdalsze (i zarazem najstarsze)
zaobserwowane galaktyki i kwazary mają przesunięcia
ku czerwieni z>5. Za najstarszy obserwowany obiekt
we Wszechświecie można uznać reliktowe promieniowanie
tła, które w chwili termodynamicznego oderwania się
od materii miało temperaturę kilku tysięcy Kelvinów
obecnie zaś ma T=2.75 K. Odpowiadające tej zmianie
temperatury przesunięcie ku czerwieni termicznego
widma tego promieniowania daje wartość 'z' rzędu 103. |