 Oddziaływania
Oddziaływania
Żadne
ciało nie jest wolne od oddziaływania innych ciał
na nie. Każdy z nas poddany jest przyciąganiu ziemskiemu,
które utrzymuje nas na powierzchni Ziemi. Różnica
temperatur powoduje nasze nagrzanie lub ochłodzenie
wywoływane oddziaływaniem termicznym.
Zawsze
jesteśmy poddawani różnym oddziaływaniom, tylko, że
są one obecne co dzień nie zdajemy sobie z nich sprawy
(np. ciśnienie atmosferyczne).
Poniżej
zajmiemy się kilkoma z nich.
Zasady
dynamiki
By
móc omawiać i analizować różne rodzaje oddziaływań
musimy zaznajomić się z zasadami jakie rządzą , i
dzięki jakim efekty oddziaływań dadzą się wyjaśnić
w logiczny sposób.
Aby badać ruch ciała wywołany
siłą na nie działającą trzeba wiedzieć jakiego rodzaju
jest to siła i skąd się bierze. Teraz zajmiemy się
ogólnymi skutkami sił a dalej będziemy rozważać specjalne
własności sił grawitacyjnych, elektromagnetycznych,
słabych i jądrowych.
W dzisiejszym rozumieniu
mechaniki klasycznej w celu rozwiązania naszego problemu
musimy:
- wprowadzić pojęcie siły F,
- ustalić sposób przypisania masy m aby opisać fakt, że różne ciała
wykonane z tego samego materiału, w tym samym otoczeniu
uzyskują różne przyspieszenia (np. pchamy z całą
siłą dwa rożne pojazdy i uzyskują różne a),
- szukamy sposobu obliczenia
sił działających na ciało na podstawie właściwości
tego ciała i otoczenia - szukamy praw rządzących
oddziaływaniami ("teorii").
Siła
Wszystkie siły nazywamy siłami rzeczywistymi, ponieważ
możemy je zawsze związać z jakimś konkretnym ciałem,
możemy podać ich pochodzenie. Nie możemy tego powiedzieć
o np. takich siłach jakich działania "doznajemy"
np. przy przyspieszaniu, hamowaniu czy zakręcaniu
samochodu? Są to siły pozorne, ponieważ nie pochodzą
one od żadnego ciała, więc nie posiadają źródła.
Pojęcie
siły:
Jeżeli
na ciało o masie m działa pojedyncza siła F1,
to definiujemy ją jako iloczyn masy na jaką działa
ta siła i przyspieszenia jakie uzyska to ciało w wyniku
działania tej siły.
F1 = ma
Zasady
dynamiki Newtona
Podstawowa
teoria, która pozwala nam przewidywać ruch ciał, składa
się z trzech równań, które nazywają się zasadami dynamiki
Newtona.
Sformułowanie pierwszej zasady dynamiki
Newtona
Ciało
pozostaje w stanie spoczynku lub w stanie ruchu jednostajnego
i prostoliniowego (zerowe przyspieszenie) gdy nie
działa na to ciało żadna siła lub wszystkie siły działające
równoważą się wzajemnie.
Ciało
pozostawione samo sobie (działająca na nie siła wypadkowa
jest równa zero).
a = 0,
gdy
Fwypadkowa =
0
gdzie
Fwypadkowa jest sumą wektorową wszystkich
sił działających na ciało.
Uwaga:
a = 0, oznacza, że nie zmienia się ani wartość ani
kierunek tzn. ciało jest w spoczynku lub porusza się
ze stałą co do wartości prędkością po linii prostej
(stały kierunek).
Pierwsza
zasada wydaje się być szczególnym przypadkiem drugiej.
Przypisujemy jej jednak wielką wagę dlatego, że zawiera
ważne prawidło fizyczne: istnienie inercjalnego układu
odniesienia.
Pierwsza zasada dynamiki
stwierdza, że jeżeli na ciało nie działają siły zewnętrzne
to istnieje taki układ odniesienia, w którym to
ciało spoczywa lub porusza się ruchem jednostajnym
prostoliniowym. Taki układ nazywamy układem
inercjalnym.
I zasada
dynamiki, układ inercjalny i nieinercjalny, siła bezwładności
I ZASADA
DYNAMIKI:
Jeżeli
na ciało nie działają żadne siły lub działające siły
równoważą się, to ciało to pozostaje w spoczynku lub
porusza się ruchem jednostajnym prostoliniowym.
UKŁAD INERCJALNY
I NIEINERCJALNY, SIŁA BEZWŁADNOŚCI
Rozpatrzmy następujące zjawisko: autobus porusza się
z przyspieszeniem 'a'. Do sufitu tego autobusu zamocowano
nić, na której końcu zawieszono metalową kulkę. Ponieważ
autobus się porusza, zaobserwujemy odchylenie się
nici od pionu w kierunku przeciwnym do kierunku ruchu
pojazdu. Rozpatrzmy to zjawisko z punktu widzenia
dwóch różnych obserwatorów, czyli z punktu widzenia
dwóch układów odniesienia. Jeden z układów, zwany
inercjalnym, jest związany z otoczeniem. Układ
ten nie posiada przyspieszenia, w nim jest obserwator
A. Drugi układ odniesienia, zwany nieinercjalnym,
jest związany z autobusem. Układ ten posiada przyspieszenie
i w nim jest obserwator B. Obserwator B, który siedzi
w autobusie, powie, że kulka, on i inne przedmioty
oraz osoby znajdujące się w autobusie, poddane są
działaniu jakiejś dodatkowej siły, zwróconej przeciwnie
do kierunku jazdy. Tę siłę nazywamy siłą bezwładności.
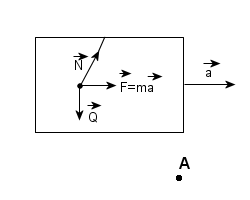
| Układ inercjalny |
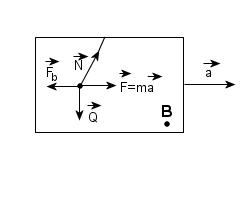
Układ nieinercjalny |
| 
|
|
| Na
kulkę działają:
siła
ciężkości Q
nić
siłą napięcia N |
Na
kulkę działają:
siła
ciężkości Q
nić
siłą napięcia N
siła
bezwładności Fb |
| Względem
A kulka porusza się z przyspieszeniem 'a',
które nadaje wypadkowa sił Q i N. |
Względem
B kulka spoczywa, więc działające na nią siły
równoważą się (wypadkowa sił Q i N równoważy
siłę Fb). |
| Układ
inercjalny to układ nieposiadający przyspieszenia;
nie działają w nim siły bezwładności. |
Układ
nieinercjalny to układ posiadający przyspieszenie;
działają w nim siły bezwładności. |
Siły bezwładności
działają jedynie w układzie nieinercjalnym. Są to
siły pozorne, ponieważ nie pochodzą one od żadnego
ciała, więc nie posiadają źródła.
Siła bezwładności ma wartość:
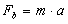
gdzie;
m - masa ciała, na które działa siła bezwładności
a - przyspieszenie układu (nie ciała, które
może mieć swoje przyspieszenie inne niż przyspieszenie
układu)
Po poznaniu układu inercjalnego można podać ogólniejszą
postać I zasady dynamiki:
Istnieje
taki układ odniesienia, w którym jeżeli na ciało nie
działa żadna siła lub siły działające na to ciało
równoważą się, to ciało zachowuje stan spoczynku lub
porusza się ruchem jednostajnym po linii prostej.
Taki układ nazywamy układem inercjalnym.
Sformułowanie drugiej zasady dynamiki
Newtona
Jeżeli na ciało działa siła niezrównoważona przez
inne siły, to porusza się ono ruchem jednostajnie
przyspieszonym z przyspieszeniem wprost proporcjonalnym
do tej siły i odwrotnie proporcjonalnym do masy ciała.
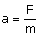
Siła w drugiej zasadzie
dynamiki jest siłą wypadkową (trzeba brać sumę wektorową
wszystkich sił).
Po co druga zasada dynamiki?
Druga zasada jest sposobem na przewidywanie przyszłości:
- mając
informację o siłach działających na ciało możemy
wyliczyć przyspieszenie tego ciała znając przyspieszenie
możemy wyliczyć prędkość chwilową tego ciała mając
prędkość możemy wyliczyć przyszłe położenie ciała
a mając nowe położenie
ciała możemy ustalić nowe siły nań działające (kółko
się zamyka)
Uwaga
Bardzo częstym błędem jest wiązanie sił działających na ciało nie
z przyspieszeniem, tylko z prędkością. Pamiętaj
siła
powoduje PRZYSPIESZENIE, a nie prędkość!!!
-
meteoryt w przestrzeni kosmicznej pędzi miliardy kilometrów,
nie zmieniając prędkości (a nie ma żadnego napędu!)
kula armatnia leci sobie długo w powietrzu mimo,
że nic jej nie napędza (artylerzyści w czasie jej
lotu często ładują i wystrzeliwują już kolejną kulę...)
do tego żeby zatrzymać rozpędzone ciało trzeba użyć
siły przeciwnie skierowanej, a nie tylko czekać
aż samo się zatrzyma kula ziemska od wielu miliardów
lat pędzi przez Kosmos z ogromną prędkością ok.
30km/s (prawie 100 razy prędkość dźwięku) mimo braku
jakiegokolwiek napędu w przypadku braku siły tarcia
(np. na lodzie) trudno jest wyhamować rozpędzone
ciało
-
zatrzymywanie się "zwykłych" ciał po pewnym czasie
wynika nie tyle z braku działania siły napędzającej,
lecz z faktu istnienia hamującej
siły tarcia!
Trzecia zasada dynamiki Newtona
Załóżmy,
że mamy układ, który składa się z mA i
mB. Wtedy jedynymi siłami będą siły oddziaływania
między tymi dwoma ciałami.
Wtedy:
Jeżeli
ciało A działa na ciało B pewną siłą F, to ciało B
działa na ciało A siłą o tej samej wartości, takim
samym kierunku, ale przeciwnym zwrocie -F.
FA→B = - FB→A
GRAWITACJA
Ciężar
ciała
Wszystkie
ciała obdarzone masą są na Ziemi przyciągane siłą
ciężkości daną wzorem:
| Q
= m . g |
m
- masa ciała
g -
przyspieszenie ziemskie
średnio g = 9,81 m/s2, w przybliżeniu 10 m/s2 |
Siła
ta nazywana jest ciężarem
ciała.
Przykład:
Ile wynosi siła ciężkości działająca na człowieka
o masie 70 kg?
Rozwiązanie:
Podstawiamy dane do wzoru na ciężar:
P
=
70 . 9,81 = 686,7 N
W
większości prostych przypadków możemy podstawiać przybliżoną
wartość przyspieszenia ziemskiego g > 10 m/s2. Dlatego w przybliżeniu
można uznać, że ciężar jest 10 razy większy od masy
ciała.
Ciężar, a masa ciała
Często
myli się pojęcie masy z pojęciem ciężaru. Potocznie
mówimy: "Ktoś waży 69 kilo". A skoro "waży",
to by oznaczało, że ciężar wyraża się w kilogramach.
Ale tak nie jest! - ciężar
"fizyczny" nie jest wyrażany w kilogramach
lecz w niutonach!
- siłę
ciężkości (ciężar) wyrażamy w niutonach
- masę
wyrażamy w kilogramach
Dlaczego nie należy utożsamiać ciężaru z masą.
W
warunkach ziemskich różnice ciężaru ciał o tych samych
masach są niewielkie. Odważnik 1 kilogramowy będzie
przyciągany siłą ok. 10 N wszędzie na naszym globie.
Jeszcze mniej waży 1 kg na Księżycu - tam z racji
znacznie mniejszego przyciągania grawitacyjnego srebrnego
globu będzie on ok. 6 razy lżejszy niż na Ziemi. Gdyby
ten sam kilogram zważyć wagą sprężynową na Jowiszu,
to okazałoby się, że jest on ponad 13 razy cięższy
niż na naszej rodzimej planecie. Jednak we wszystkich
tych miejscach masa ciężarka jest tak sama i wynosi
cały czas 1 kg.
Prawo
powszechnego ciążenia
Prawo
powszechnego ciążenia
(inaczej: prawo grawitacji) sformułował Izaak
Newton w 1687 r., a brzmiało ono:
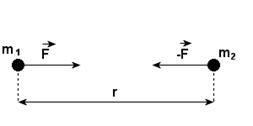
Każde dwa punkty materialne o masach 'm1'
i 'm2' przyciągają się wzajemnie
siłą wprost proporcjonalną do iloczynu ich mas, a
odwrotnie proporcjonalną do kwadratu ich odległości.
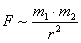
Aby znak
proporcjonalności zastąpić równością, wprowadzamy
współczynnik G, zwany stałą grawitacji.
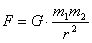
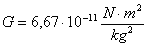
Masami
'm1' i 'm2' mogą
być też ciała, które nie są punktami materialnymi
mogą to być np. dwie planety.
Siły grawitacji
wywołują przyspieszenia zwane grawitacyjnymi, charakteryzujące
się tym, że są niezależne od masy ciała przyspieszanego.
Duży kamień spada (w próżni) z takim samym przyspieszeniem,
jak ziarnko piasku.
Siła grawitacji
jest niezmiernie słaba.
Weźmy taki
przykład: na dwu sąsiednich torach towarowej stacji
kolejowej stoją dwa wagony, zawierające każdy po 30
ton węgla. Jaka siła grawitacji działa między tymi
dwoma wagonami? Prosty rachunek może wskazać, że jest
to siła równa ciężarowi liczącemu ułamki grama. Istotnie
więc siła grawitacji jest oddziaływaniem bardzo słabym.
Ale z drugiej strony przeczy temu nasze codzienne
doświadczenie. Upadek z wysokości kilku zaledwie metrów
doprowadza do takiej prędkości, że może to grozić
połamaniem kości. Skąd ten paradoks? Wyjaśnia go niewyobrażalnie
wielka masa Ziemi w porównaniu z przedmiotami, z jakimi
spotykamy się w życiu codziennym. Oczywiście w porównaniu
z masami Słońca, czy innych gwiazd, masa Ziemi jest
po prostu mała.
Kwadrat odległości dwu ciał we wzorze na siłę grawitacji
oznacza, że w miarę oddalania się dwu ciał przyciągających
się, siła oddziaływania grawitacyjnego między nimi
szybko maleje. Czy ten efekt obserwujemy w naszym
życiu codziennym? A jeśli nie, to dlaczego? Oto po
prostu dlatego, że środek ciężkości naszej Ziemi jest
odległy od jej powierzchni o ponad 6300 km, a więc
wzniesienie się o np. 10 m (np. wejście na trzecie
piętro) zmniejsza siłę grawitacji o kilka tysięcznych
części promila. A więc i tu stwierdzenie, że grawitacja
szybko maleje z odległością, odnosi się do skali astronomicznej,
a nie do warunków naszego życia codziennego. |