 Co to jest
entropia?
Co to jest
entropia?
Entropia
jest termodynamicznym parametrem stanu układu.
W interpretacji statystycznej, określa ona stopień
nieuporządkowania układu, albo inaczej mówiąc,
stopień jego wyjątkowości. Statystycznie określa
się ją jako:
Gdzie
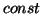 jest jakąś stałą. jest jakąś stałą. 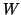 natomiast jest definiowane
jako liczba mikrostanów nieodróżnialnych od naszego
makrostanu. Z tego wynika np. że wazon ma małą
entropię (nieuporządkowanie), natomiast rozbite
odłamki dużą (jest wiele możliwych realizacji
rozbitego wazonu). natomiast jest definiowane
jako liczba mikrostanów nieodróżnialnych od naszego
makrostanu. Z tego wynika np. że wazon ma małą
entropię (nieuporządkowanie), natomiast rozbite
odłamki dużą (jest wiele możliwych realizacji
rozbitego wazonu).
Interpretacja
statystyczna jest ściśle związana z entropią znaną
z teorii informacji. Tam używa się tego pojęcia
do opisywania źródeł, generujących komunikaty.
Entropia określa na ile nie potrafimy przewidzieć
co źródło wygeneruje. Funkcja entropii musi spełniać
4 aksjomaty, warunkujące jej stosowalność jako
miarę opisu nieokreśloności. Okazuje się, że jedyną
postacią funkcji, jest tu
Gdzie
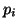 to prawdopodobieństwa wygenerowania przez źródła
kolejnych komunikatów. to prawdopodobieństwa wygenerowania przez źródła
kolejnych komunikatów.
Z punktu
widzenia przemian termodynamicznych, entropię
definiuje się jako uogólnione przemieszczenie.
Dla siły i pracy można napisać zależność:
Podobne
równanie można zapostulować dla całkowitego pochłoniętego
ciepła (odpowiednik pracy z powyższego wzoru)
i jednostki napędowej (temperatura), zużytej na
,,uogólnionej drodze'' (entropii):
Przy
czym ciepło całkowite jest równe ciepłu zużytemu
na tarcie i rzeczywiście wchłoniętemu:
Można
udowodnić, że entropia jest funkcją stanu. Tzn.
nie zależy ona od drogi, po jakiej się do niej
doszło.
Entropia
jest jedną z zasadniczych wielkości używanych
w termodynamice; jest treścią niezwykle ważnej,
drugiej zasady termodynamiki, mówiącej że w przyrodzie
entropia może jedynie wzrastać. Jeśli maleje lokalnie,
to nie ma siły-w tym samym czasie gdzieś musi
wzrosnąć, aby sumarycznie entropia nie malała.
Na
ogół w przemianach termodynamicznych nie interesuje
nas entropia jako taka, ale jej zmiany. Sprawa
jest podobna do energii potencjalnej: poziom zerowy
jest przyjmowany umownie. W przypadku entropii
jest on zgodnie z postulatem Plancka przyjmowany
dla doskonałych kryształów na poziomie temperatury
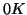 , co umożliwia wyzerowanie stałej, obecnej w interpretacji
statystycznej. W temperaturze , co umożliwia wyzerowanie stałej, obecnej w interpretacji
statystycznej. W temperaturze 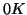 istnieje bowiem zgodnie z
zasadami fizyki kwantowej tylko jeden mikrostan
( istnieje bowiem zgodnie z
zasadami fizyki kwantowej tylko jeden mikrostan
(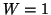 ). ).
Rysunek
8.1:
Obieg w
silniku iskrowym-obieg Otto
| |
Przy
analizowaniu przemian termodynamicznych na wykresach,
pole pod krzywą entropii (na wykresie T-S) określa
pochłaniane lub wydawane ciepło. Modelowe obiegi
termodynamiczne (silniki spalinowe, siłownie parowe)
składają się w dużej części przypadków z przemian
izentropowych (lub prawie izentropowych) (np.
przemiana adiabatyczna-jeśli podstawić do wzoru
8.5 ,,brak wymiany ciepła'', dostaniemy 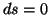 ) i przemian zwiększających
entropię (np. izotermiczna (w idealnym silniku
Carnota i w siłowniach parowych), izobaryczna
i izochoryczna (w silnikach spalinowych-obiegi
Otto i Diesla). ) i przemian zwiększających
entropię (np. izotermiczna (w idealnym silniku
Carnota i w siłowniach parowych), izobaryczna
i izochoryczna (w silnikach spalinowych-obiegi
Otto i Diesla).
Prześledźmy
dla przykładu obieg Otto (rysunek 8.1). Z lewego
dolnego rogu do góry następuje sprężanie adiabatyczne
czynnika. Podwyższa się jego temperatura, ale
proces jest na tyle szybki, że nie ma wymiany
ciepła z otoczeniem. Następnie powstaje zapłon,
mieszanka wybucha i izochorycznie (objętość tłoka
jest stała, a szybkość wybuchu bardzo duża) oddaje
ciepło (wzrasta ciśnienie). Następnie (odcinek
pionowy prawy) następuje adiabatyczne rozprężanie
spalin, a potem ich wydmuchnięcie i oziębienie
w otoczeniu (dolny odcinek poziomy). Całkowita
praca jest równa polu wewnątrz krzywej. Widać,
że istnieją straty towarzyszące wydalaniu spalin.
(zastrzeżenie:
entropię można definiować również dla obiektów
bez wymiany ciepła)
Jest
sobie wyrażenie 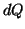 , które stanowiło dla termodynamików
problem - czemu?, bo nie jest funkcją stanu -
czyli taką, której wartość zależy nie od ,,drogi
przejścia'' a od stanu początkowego i końcowego
danego procesu (np jest jakiś reaktor przepływowy
i nie wiadomo co się w środku dzieje - jak masz
funkcję stanu to zmierzysz parametry na wejsciu,
na wyjściu i coś wiesz, nie korzystając z funkcji
stanu musiał byś analizować ,,środek'' reaktora)
- matematycznie funkcja taka nie posiada różniczki
zupełnej, więc mądre głowy (dokładniej Clausius)
szukały wyrażenia, przez które pomnożona różniczka
ciepła stała by się różniczką zupełną (tzw. czynnik
całkujący) jednocześnie wyrażenie to powinno być
zależne od jak najmniejsze ilości termodynamicznych
parametrów stanu (ciśnienie, temperatura, objętość)
czynnik ten pozwala określić funkcję stanu , które stanowiło dla termodynamików
problem - czemu?, bo nie jest funkcją stanu -
czyli taką, której wartość zależy nie od ,,drogi
przejścia'' a od stanu początkowego i końcowego
danego procesu (np jest jakiś reaktor przepływowy
i nie wiadomo co się w środku dzieje - jak masz
funkcję stanu to zmierzysz parametry na wejsciu,
na wyjściu i coś wiesz, nie korzystając z funkcji
stanu musiał byś analizować ,,środek'' reaktora)
- matematycznie funkcja taka nie posiada różniczki
zupełnej, więc mądre głowy (dokładniej Clausius)
szukały wyrażenia, przez które pomnożona różniczka
ciepła stała by się różniczką zupełną (tzw. czynnik
całkujący) jednocześnie wyrażenie to powinno być
zależne od jak najmniejsze ilości termodynamicznych
parametrów stanu (ciśnienie, temperatura, objętość)
czynnik ten pozwala określić funkcję stanu 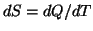
Co
do filozofii wzrostu entropii pozwolę sobie napisać,
że w przyrodzie są prawdopodobne tylko takie zjawiska,
podczas których: suma przyrostów entropii wszystkich
ciał uczestniczących w zjawisku jest większa od
zera (to jest bardzo istotna różnica).
Są
też inne definicje entropii, ale moim zdaniem
podana wyżej może być traktowana jako pierwotna,
gdyż to termodynamicy pierwsi zajęli się tym problemem
a pojęcie entropii chyba właśnie w tej formie
jest najszerzej stosowane (od rafinacji metali
do analizy obiegów cieplnych).
|