DLACZEGO NIEBO JEST CIEMNE?

Do wykonania jednej z najbardziej podstawowych obserwacji kosmologicznych nie trzeba wielkich teleskopów, nie trzeba wielu nocy obserwacji. Wystarczy jedna gwiaździsta noc... i chwila zastanowienia. Zastanowienia nad tym, dlaczego niebo jest gwiaździste.

W okresie, kiedy Almagest Klaudiusza Ptolemeusza stanowił podstawę wiedzy astronomicznej, zastanowienie takie wydawało się zbyteczne. Wszechświat stanowił jedną olbrzymią, puszczoną w ruch machinę, której centrum stanowiła nieruchoma Ziemia, najdalszym ograniczeniem zaś była sfera gwiazd stałych, poza którą już nic być nie mogło. Zgodnie z koncepcjami Arystotelesa, które legły u podstaw tego modelu, przestrzeń pozbawiona materii nie istnieje, tak więc przedstawiony model Wszechświata był skończony, ograniczony przestrzennie. W modelu takim skończona liczba gwiazd przyczepionych do ostatniej sfery nie budzi zdziwienia. Warto nadmienić, że już starożytni atomiści z Demokrytem na czele głosili, że Wszechświat składa się z nieskończonej ilości poruszających się atomów, że atomy te, jak w pojemniku, muszą poruszać się w nieskończenie rozciągłej pustej przestrzeni, poglądy te jednak nie zostały zaakceptowane przez współczesnych i nie były w stanie konkurować przez stulecia z klasycznym modelem geocentrycznym. Dopiero Newtonowi zawdzięczamy odrodzenie koncepcji nieskończonego (przestrzennie) Wszechświata, tym razem już na bazie ścisłych sformułowań mechaniki, a nie spekulacji filozoficznych. Ugruntowane przez Newtona koncepcje absolutnej przestrzeni i absolutnego czasu zapanowały na długo (aż do narodzin obu teorii względności: szczególnej i ogólnej) w fizyce. Przestrzeń kosmiczna istniała u Newtona jak gdyby nieskończenie rozciągły pojemnik, obdarzony właściwościami geometrycznymi (oczywiście obowiązywała geometria euklidesowa, bo jakaż by mogła być inna), ale nie fizycznymi, wypełniony różnego rodzaju ciałami niebieskimi. A oto jak Newton uzasadniał sam nieskończoność Wszechświata:

"Gdyby cała materia naszego Słońca i planet i wszelka w ogóle materia we Wszechświecie rozłożona była równomiernie na niebie, każda zaś cząstka wykazywała właściwe sobie ciążenie ku pozostałym, jednocześnie cały obszar przestrzeni wypełniony tą rozmieszczoną w nim materią był skończony, wtedy materia znajdująca się w zewnętrznych częściach tego obszaru dążyłaby w rezultacie własnej ciężkości ku materii wypełniającej jego wnętrze. Spadałaby więc ona w kierunku do środka całej przestrzeni, w wyniku czego powstałaby tam jedna wielka kulista masa. Gdyby jednak materia rozłożona była równomiernie w przestrzeni nieskończonej, nigdy nie mogłaby zebrać się w jednej bryle. Część jej mogłaby utworzyć jedną masę, część zaś inną, i w ten sposób postałaby nieskończona liczba wielkich mas rozrzuconych w dużych odległościach wzajemnych w całej tej nieskończonej przestrzeni. I tak właśnie powstać mogło Słońce i gwiazdy stałe" (Isaac Newton w liście do Richarda Bentleya z 10 grudnia 1692 r.).

Rozumienie Newtona stanowiło próbę wyjaśnienia dlaczego "wbrew" siłom powszechnego ciążenia powstało wiele ciał niebieskich zamiast jednego.

Nieskończoność przestrzeni ratowała w tym ujęciu Wszechświat przed zapaścią grawitacyjną do jednego miejsca. Ale rodziły się inne trudności, na które kolejno zwracali uwagę Halley i de Ch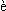seaux, aż wreszcie wyraźnie sformułował je Olbers (Dlaczego w nocy niebo jest ciemne, skoro patrząc w każdym kierunku patrzę na jakąś gwiazdę?).

Stąd nazwa: paradoks Olbersa.

Pod nazwą paradoksu fizykalnego rozumie się twierdzenie wysnute z podstawowych praw fizyki, lecz prowadzące do wniosków sprzecznych z wynikami obserwacji lub doświadczenia. Paradoksem w tym sensie był właśnie paradoks fotometryczny, jak niekiedy nazywa się paradoks Olbersa. Powtórzmy w uproszczeniu rozumowanie Olbersa, pochodzące sprzed ponad półtora wieku. Oto podstawowe założenia newtonowskiego modelu nieskończonego Wszechświata, z których w rozumowaniu swym wychodził Olbers:

I. Wszechświat jest nieskończony przestrzennie i niezmienny w czasie.

II. W tej nieskończonej przestrzeni gwiazdy są rozłożone (średnio, ma się rozumieć) w sposób równomierny, liczba ich zaś jest nieskończona.

III. Średnia na jednostkę objętości Wszechświata jasność gwiazd jest jednakowa. (To założenie okaże się nieistotne dla przeprowadzonego rozumowania).

Newtonowski model stanowił nieskończony, jednorodny, statyczny Wszechświat. Każdy punkt w tym Wszechświecie może być uważany za jego środek, żaden bowiem nie jest wyróżniony. Weźmy dowolny punkt P (ten na przykład, w którym się znajdujemy) i zatoczmy wokół niego dwie powierzchnie kuliste, odpowiednio o promieniach r oraz r + Δr (jak na rysunku).

Oznaczmy literą M moc średnią pojedynczej gwiazdy, a literą N - liczbę gwiazd w jednostce objętości. Bierzemy oczywiście tak dużą jednostkę objętości, by wszelkie ewentualne fluktuacje gęstości rozmieszczenia gwiazd przestały odgrywać rolę. Objętość zawarta między obu zatoczonymi powierzchniami (przy
założeniu r >> Δr ) równa jest 4 r ² Δr , w niej znajduje się łącznie 4 r² N Δr gwiazd, których łączna moc promieniowania wynosi 4 r² N ΔrM . Wiadomo, że natężenie promieniowania spada z kwadratem odległości, zatem z całej zaznaczonej objętości między obu powierzchniami kulistymi dociera do obserwatora w punkcie P w jednostce czasu tylko 1/ r² część promieniowania:

(1/ r² ) (4 r² N ΔrM ) = 4 NM Δr.

Widać stąd, że ilość światła, docierająca w jednostce czasu do obserwatora w punkcie P z warstwy kulistej o promieniu r , nie zależy od promienia tej warstwy. Jeśli tylko grubości 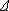r dalszych warstw są takie same, to z każdej z nich dochodzi ta sama ilość światła. Obrazowo mówiąc, to co tracimy na natężeniu światła z pojedynczej gwiazdy (w wyniku spadku natężenia z kwadratem odległości), kompensuje nam wzrost (znów z kwadratem odległości) średniej liczby gwiazd w warstwie. Jeśli dodawać będziemy natężenia promieniowania z kolejnych warstw, to w nieskończonym Wszechświecie dostaniemy sumę nieskończenie wielu identycznych wyrazów (różnych od zera), a więc będzie to wielkość nieskończona. Ponieważ spodziewamy się, że prędzej czy później promień wyprowadzony z punktu P w jakimkolwiek kierunku zakończyć się musi na jakiejś gwieździe, więc całe niebo powinno być rozświetlone do jasności równej jasności pojedynczej gwiazdy. Tymczasem niebo jest czarne w nocy. Dlaczego tak jest?

Nad zagadnieniem tym jeszcze przed Olbersem myślał de Ch 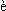seaux, któremu wydawało się, że znalazł wyjaśnienie. Obłoki ciemnej materii (pyłu) mogłyby zakrywać odległe gwiazdy. Było to jednak wyjaśnienie pozorne. Olbers poszedł dalej, rozpatrując krytycznie, co będzie się dziać z obłokiem, pochłaniającym padające nań promieniowanie. Obłok taki będzie się stopniowo nagrzewać, w końcu temperatura jego wzrośnie, ale wtedy i on będzie promieniować, rozżarzy się. Wiemy dziś, że przy ustaleniu się równowagi obłok taki będzie wypromieniowywać tyle energii, ile sam dostaje (choć może być to w innym zakresie widma). Tak więc ani wprowadzenie przesłaniających obłoków, ani też innych ciemnych (czy jasnych) ciał na drodze promieniowania, docierającego do nas, nie jest w stanie usunąć paradoksalnej konsekwencji rozumowania. Jeśli tak, to może któreś z założeń jest błędne? Okazało się, że trzecie założenie jest nieistotne dla rozumowania. Więc albo założenie I, albo też II jest błędne. Znaczy to, że albo przestrzeń nie jest nieskończona, albo skończoną jest przynajmniej liczba gwiazd w nieskończonej przestrzeni. Od chwili sformułowania paradoksu fotometrycznego przez Olbersa w 1823 roku usiłowano doprowadzić do zgodności między newtonowską koncepcją nieskończonego Wszechświata a obserwacją nocnego nieba. Wymyślano różne sposoby uniknięcia paradoksu. A tu jak na złość, przybył jeszcze jeden paradoks: paradoks grawitacyjny, przypisywany H. von Seeligerowi. Polega on na tym, że jeśli przyjąć równomierny (średnio) rozkład gwiazd w nieskończonej przestrzeni, wtedy w dowolnym punkcie tej przestrzeni każda masa ma nieskończoną energię potencjalną. I chociaż mamy zupełną swobodę w wyborze zerowego poziomu energii, to w opisanej sytuacji napotkalibyśmy na fundamentalne trudności przy próbach uznania jakiegokolwiek układu odniesienia za układ inercjalny. A przecież istnienie choć jednego układu inercjalnego jest podstawą całej mechaniki Newtona.

Aby wytłumaczyć paradoksy, uciekano się do takich hipotez, jak np. przyjęcie, że siła ciążenia maleje nie z kwadratem odległości, a nieco szybciej. Paradoksów można by też uniknąć, gdyby przyjąć, że obserwator w punkcie P - to obserwator w miejscu wyróżnionym, w którego okolicy najwięcej jest gwiazd w jednostce objętości. W takim razie byłby to punkt wyróżniony, który można by nazwać środkiem Wszechświata. A przecież już od decydującego kroku Kopernika, który położył kres systemowi geocentrycznemu, kosmologowie dochodzili do uznania, że nasze położenie (tj. położenie Ziemi, Słońca, Galaktyki, gromady galaktyk, w której się znajdujemy) jest typowe, niczym nie wyróżnione. Aby uniknąć powrotu do koncepcji wyjątkowości położenia sformułowali oni nawet specjalną zasadę, w myśl której obraz Wszechświata i zjawisk w nim nie zależy od położenia obserwatora. Zasada ta pozwoliła na dokonanie postępu przez rozszerzanie ziemskich praw fizyki, przez łatwe ekstrapolowanie obserwacji astronomicznych. Czy warto z tej zasady rezygnować? (W jednym z dalszych artykułów powiemy coś więcej o tej tzw. zasadzie kosmologicznej).

Choć przy formułowaniu paradoksu Olbersa mówiliśmy o gwiazdach, równie dobrze można na ich miejsce podstawić galaktyki. Istota paradoksu nie ulegnie zmianie.

Nie chciałbym, aby w Czytelnikach tego artykułu wyrobić się miało przekonanie, iż paradoksu Olbersa nie udało się rozwiązać na gruncie newtonowskiego statycznego modelu nieskończonego Wszechświata z geometrią euklidesową. Rozwiązanie takie udało się szwedzkiemu astronomowi Charlierowi na początku XX wieku. Stworzył on model hierarchicznego Wszechświata. Był to twór statyczny, nieskończony, złożony z gromad kolejnych rzędów. Z gromad rzędu pierwszego (np. gwiazd) tworzyły się gromady rzędu drugiego (galaktyki), z tych gromady rzędu trzeciego, i tak dalej w nieskończoność. Średnia gęstość materii w gromadach kolejnych rzędów maleje przy tym w określony sposób (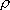_i = 3 M_i /4 R_i ³) gdzie M i , R_i i r_i oznaczają, odpowiednio, całkowitą masę, promień i gęstość gromady i -tego rzędu. Pozwala to na usunięcie i paradoksu grawitacyjnego, i fotometrycznego. Brakuje dziś przekonywających danych obserwacyjnych na rzecz modelu hierarchicznego Charliera, ponadto oba wspomniane paradoksy znacznie prościej tłumaczy się w ramach kosmologii einsteinowskiej rozszerzającego się Wszechświata.

A teraz Czytelniku, przyznaj się przed sobą samym: Czy zdziwiło Cię kiedykolwiek, że niebo jest czarne? Pamiętaj: zdziwienie to droga do paradoksów... i odkryć. Dziwią się dzieci (zanim je życie oduczy)... i geniusze.

Edmund Halley (1656-1742), astronom angielski, profesor uniwersytetu w Oxfordzie, dyrektor obserwatorium w Greenwich. Współpracował blisko z Newtonem, wydał jego Philosophiae naturalis principia mathematica . Obliczał orbity komet, odkrywając przy tym istnienie kometarnych eliptycznych orbit okresowych (np. nazwana jego imieniem kometa Halleya o okresie obiegu wokół Słońca wynoszącym 76 lat). W 1718 r. odkrył istnienie ruchów własnych gwiazd. Był autorem stosowanej w XVIII wieku metody wyznaczania odległości Słońca od Ziemi z obserwacji przejść Wenus przed tarczą słoneczną. Oto jego wypowiedź z 1720 roku w interesującej nas sprawie: "Gdyby liczba gwiazd stałych była większa od skończonej, wtedy cała powierzchnia ich pozornej sfery (tj. niebo - przypisek B.K.) powinna być jasna".

Jean Philippe L. de Ch 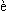seaux (1718-1751), astronom szwajcarski, napisał w książce Trait 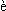de la comete qui a paru en d 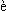cembre 1743 (wydanej w Paryżu w 1744 r.): "Jeśli ilość gwiazd we Wszechświecie jest nieskończona, to dlaczego całe niebo nie jaśnieje jak powierzchnia pojedynczej gwiazdy? Dlaczego niebo jest ciemne? Dlaczego gwiazdy oddzielone są ciemnymi obszarami?". Nie mając jednak odwagi posunąć się zbyt daleko w swych wątpliwościach, de Ch seaux usiłuje odpowiedzieć na nie sam sobie: "Najpewniej chyba obłoki pyłu kryją przed nami światło odległych gwiazd. Do obserwatorów ziemskich dociera tylko promieniowanie z najbliższych gwiazd".

Heinrich Eilhelm Matthias Olbers (1758-1840), lekarz z zawodu, żył i pracował w Bremie, stał się jednym z najwybitniejszych astronomów początku XIX w. (za Wielką Encyklopedią Powszechną PWN ). Odkrył dwie małe planety: Pallas i Westę, oraz sześć komet. Rozwiązał problem wyznaczania parabolicznej orbity komety, podał teorię powstania małych planet z rozpadu pierwotnej większej planety.

Hugo von Seeliger (1849-1924), dyrektor obserwatorium monachijskiego. Opracował statystycznie kwestię rozkładu przestrzennego gwiazd w otoczeniu Słońca. Prace jego nad paradoksem grawitacyjnym ukazały się w latach 1895-96.

Carl Wilhelm Ludwig Charlier (1862-1934), astronom szwedzki, pracujący głównie nad kinematyką gwiazd. Pierwsza próba zbudowania modelu hierarchicznego, nieskończonego Wszechświata statycznego przedstawiona została w jego pracy Wie eine unendliche Welt aufgebaut sein kann z 1908 roku.

Źródło: http://www.wiw.pl/