Zderzenia

Zderzenie można zdefiniować jako - krótkotrwałe, silne oddziaływanie wzajemne zderzających się ciał przy ich zetknięciu się ze sobą, w wyniku czego doznają one zmiany prędkości.

A więc pojęcie "zderzenie" opisuje zmianę ruchu zderzających się ciał (lub przynajmniej jednej z nich). Zmiana ta zachodzi bardzo gwałtownie, więc można oddzielić przebieg zjawiska przed zderzeniem od przebiegu zjawiska po zderzeniu.

Daje nam to możliwość badania ruchów ciał ulegających zderzeniom. Jeśli znamy ruch ciał przed zderzeniem, i wiemy, że podczas zderzenia musi zostać spełniona zasada zachowania pędu i zasada zachowania całkowitej energii, to potrafimy znaleźć ruch tych ciał po zderzeniu.

Omówiony zostanie tu przykład zderzających się sprężyście kul.

Zderzenia klasyfikuje się na podstawie tego czy energia kinetyczna jest zachowana podczas zderzenia, czy też nie.

- Zderzenie jest sprężyste, gdy energia kinetyczna jest w zderzeniu zachowana.

- Gdy energia kinetyczna układy zmienia się podczas zderzenia, to zderzenie takie jest niesprężyste .

Zderzenia sprężyste jak i niesprężyste mogą być centrale lub niecentralne.

Zderzenia centralne to szczególny przypadek zderzeń, w których prędkości zderzających się ciał skierowane są wzdłuż prostej łączącej ich środki. Wszystkie inne przypadki zderzeń będą zderzeniami niecentralnymi lub inaczej skośnymi.

Zderzenia sprężyste.

Najprostszym przypadkiem zderzenia jest zderzenie sprężyste centralne.

Zakładamy że dwie zderzające się kule o masach m₁ i m₂ poruszają się w tym samym kierunku przed i po zderzeniu. Prędkości kul przed zderzeniem oznaczamy v p₁ i v p₂ a po zderzeniu v_k1 i v_k2 . jeżeli więc zasada zachowania energii kinetycznej musi zostać spełniona to :

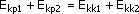
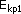- energia kinetyczna kuli 1 przed zderzeniem

- energia kinetyczna kuli 2 przed zderzeniem

- energia kinetyczna kuli 1 po zderzeniu

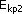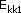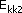- energia kinetyczna kuli 2 po zderzeniu

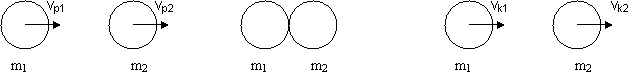
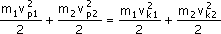
Ponieważ w tym przypadku kule nie zmieniają kierunku swego ruchu oraz zwrotów swych prędkości to postać wektorowa zasady zachowania pędu jest identyczna z postacią skalarną.

Mamy więc: m₁ v_p1 + m₂ v_p2 = m₁ v_k1 + m₂ v_k2

m₁ v²_p1 + m₂ v²_p2 = m₁ v²_k1 + m₂ v²_k2

grupujemy po jednej stronie równań wyrazy z m1 a po drugiej z m2, oraz korzystając z tego, że różnica kwadratów dwóch wielkości jest równa iloczynowi sumy tych wielkości i ich różnicy, otrzymamy układ równań:

m₁(v_p1- v_k1)(v_p1+ v_k1) = m₂(v_k2- v_p2)(v_k2+ v_p2) **

m₁(v_p1- v_k1) = m₂ (v_k2- v_p2) *

Równania te dzielimy stronami przez siebie. Otrzymujemy:

v_p1 + v_k1 = v_k2 + v_p2

Obliczając z tego v_k2 i wstawiając otrzymane wyrażenie do równania z * możemy wyznaczyć wartość prędkości kuli 1 po zderzeniu.

Tą zależność wstawiamy do równania z ** . Otrzymujemy:

Równania na v_k1 i v_k2 przedstawiają ogólne rozwiązanie problemu zderzeń sprężystych. Można je zastosować do dowolnych przypadków szczególnych.

1. Np. Kula 2 znajdowała się w spoczynku przed zderzeniem, czyli v_p2 = 0, więc

2. Jeżeli teraz kula 2 poruszała się przed zderzeniem naprzeciw kuli 1 to przyjmując prędkość pierwszej kuli za dodatnią, prędkość kuli 2 będzie miała znak ujemny. Otrzymujemy:

3. Gdy masy kul będą sobie równe, wtedy v_k1 = - v_p2 oraz v_k2 = v_p1 .

Oznacza to, że kule wymienią między sobą swoje prędkości. Kula pierwsza będzie się poruszała z prędkością początkową kuli drugiej i w tę stronę, w którą poruszała się przed zderzeniem kula druga. Kula druga natomiast będzie się poruszała z prędkością początkową kuli pierwszej w stronę, w którą poruszała się przed zderzeniem kula pierwsza.

Zderzenia niesprężyste

Rozpatrujemy warunki zderzenia jw., lecz tym razem będzie to zderzenie niesprężyste.

Podczas zderzeń niesprężystych kule doznają trwałych odkształceń a praca wykonana przy odkształceniu nie może zostać zwrócona do układu.

Oznacza to, że zasada zachowania energii mechanicznej nie może w tym przypadku zostać spełniona. Zasada zachowania pędu spełniona zostaje we wszystkich przypadkach zderzeń a więc także w tym.

Rozpatrzmy przypadek idealnie niesprężystego, centralnego zderzenia kul poruszających się z prędkościami zwróconymi w jedną stronę. W wyniku zderzenia kule przyklejają się do siebie i dalej poruszają się razem.

Mamy więc:

m₁ v_p1 + m₂ v_p2 = (m₁ + m₂) v_k

oraz

Wyrażenie to pozwala wyznaczyć prędkość końcową obu kul.