|
 Pole
magnetyczne cz. II
Pole
magnetyczne cz. II
1.
Pole magnetyczne przewodników z prądem
Obok
przewodnika ustawiamy igłę magnetyczną. Gdy przez
przewodnik nie płynie prąd, igła wskazuje kierunek
północ - południe. Gdy do przewodnika podłączymy napięcie
powodując przepływ prądu, obserwujemy odchylenie się
igły magnetycznej od kierunku pierwotnego. Zatem:
Wokół przewodnika w którym płynie prąd występuje pole
magnetyczne .
A)
Pole magnetyczne wokół przewodnika prostoliniowego
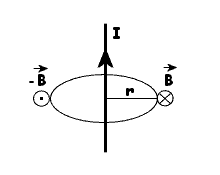
Wielkościami
informującymi o tym jak silne jest pole magnetyczne
są: natężenie pola H i indukcja magnetyczna B . Na
podstawie reagowania igły magnetycznej stwierdzimy,
że natężenie pola magnetycznego przewodnika jest tym
większe, im większe jest natężenie prądu w przewodniku
i im mniejsza jest odległość punktu pola do przewodnika.
Zatem:
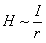
Aby
napisać równość wprowadzimy współczynnik proporcjonalności,
który dla przewodnika nieskończenie długiego wynosi
1/2π . Tak więc natężenie pola magnetycznego
wokół tego przewodnika ma wartość:
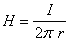
Z
tego wzoru możemy wyznaczyć jednostkę natężenia pola
magnetycznego:
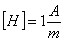
Indukcja
magnetyczna:
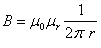
Natężenie
pola magnetycznego i indukcja są to wektory styczne
do linii pola. Kształt linii pola zbadamy za pomocą
opiłków żelaza posypanych na płytkę prostopadłą do
przewodnika. Opiłki te utworzą okręgi współśrodkowe.
Zwrot linii określamy za pomocą reguły śruby prawoskrętnej
.
Gdy w sąsiedztwie znajduje się kilka przewodników
z prądem, zachodzi superpozycja pól. Natężenie pola
i indukcja magnetyczna są wypadkowymi poszczególnych
pól składowych.
B)
Pole magnetyczne wokół przewodnika kołowego
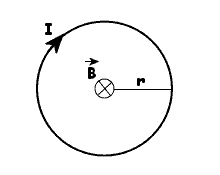
Przypadek
ten jest bardzo podobny do poprzedniego, więc ograniczymy
się tylko do podania wzorów:
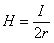
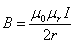
C)
Pole magnetyczne solenoidu
Solenoid
jest zwojnicą składającą się z przewodników kołowych
połączonych szeregowo. Zajmować się będziemy solenoidem
długim i składającym się ze zwojów nawiniętych jednowarstwowo
i gęsto.
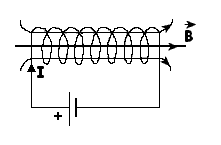
Za
pomocą igły magnetycznej wykazujemy istnienie pola
magnetycznego wokół solenoidu. Za pomocą opiłków żelaza
badamy kształt linii pola magnetycznego. Regułą zwiniętej
prawej dłoni wyznaczamy zwrot linii pola.
Pole magnetyczne wewnątrz solenoidu uznajemy za jednorodne
, zaś na zewnątrz podobne jest ono do pola wokół magnesu
sztabkowego, dlatego polu solenoidu przypisujemy dwa
bieguny.
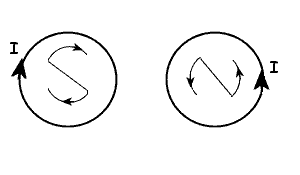
Zasadę
oznaczania biegunów w solenoidzie przedstawia mam
nadzieję w sposób jasny rysunek obok. Strzałki, które
tworzą litery biegunów, muszą zmierzać ku końcom tych
liter zgodnie z kierunkiem prądu.
Natężenie
wewnątrz solenoidu jest wprost proporcjonalne do natężenia
prądu I i ilości zwojów n,
a odwrotnie proporcjonalne do długości solenoidu l
:
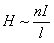
Współczynnik
proporcjonalności wynosi 1, więc natężenie wewnątrz
solenoidu wynosi:
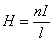
Indukcja
magnetyczna:
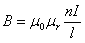
2.
Strumień magnetyczny
O
strumieniu magnetycznym mówimy wtedy, gdy przez jakąś
powierzchnię przepływają linie pola magnetycznego.
Załóżmy, że w polu jednorodnym przez pewną powierzchnię
płaską przepływa strumień. Strumień magnetyczny (lub
strumień indukcji magnetycznej ) jest definiowany
wzorem:
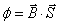
|
lub
|
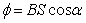
|
gdzie
α jest kątem pomiędzy wektorami B
i S . Wektor S ma wartość równą polu
powierzchni, przez którą przepływa strumień i jest
do tej powierzchni prostopadły. Wektory B
i S mnożymy przez siebie skalarnie,
więc strumień indukcji magnetycznej jest skalarem.
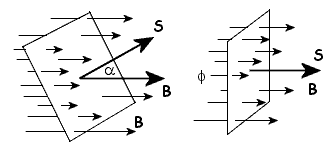
Na
drugim rysunku widzimy, że kąt między wektorami B
i S wynosi 0°, zatem wzór na strumień magnetyczny
możemy zapisać w następujący sposób:
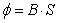
Jednostką
strumienia indukcji magnetycznej jest weber .
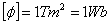
1
weber ( Wb ) jest to strumień indukcji magnetycznej
przepływający prostopadle przez powierzchnię 1 m 2
w jednorodnym polu magnetycznym o indukcji
1 T (tesli).
3.
Oddziaływanie przewodników z prądem,
amper absolutny
Dane
są dwa równoległe prostoliniowe nieskończenie długie
przewodniki z prądem. Gdy przez te przewodniki płynie
prąd (w praktyce o dużym natężeniu ), to przewodniki
te działają na siebie wzajemnie. Przyciągają się,
gdy prąd płynie w obu przewodnikach w jednym kierunku
i odpychają się, gdy prąd płynie w kierunkach przeciwnych.
Dzieje się tak, bo wokół każdego przewodnika istnieje
pole magnetyczne i znajduje się on w polu magnetycznym
drugiego, dlatego na każdy przewodnik działa siła
elektrodynamiczna .
Rozpatrzymy
przewodniki z prądem płynącym w jednym kierunku.
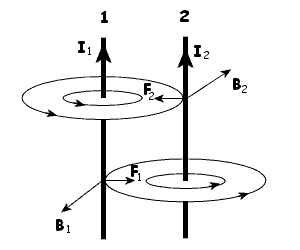
Rozpatrzmy
przewodnik 2. Przepływają przez niego linie pola przewodnika
1 od przodu (za rysunek). Za pomocą reguły Fleminga
stwierdzimy, że na przewodnik 2 działa siła F2
leżąca w płaszczyźnie rysunku i zwrócona w lewo. Przewodnik
1 jest przekłuwany przez linie pola przewodnika 2
od tyłu (zza rysunku). Regułą Fleminga wyznaczamy
zwrot siły działającej na przewodnik 1. Siła F1
działa w prawo. Rozpatrywane przewodniki przyciągają
się.
W podobny sposób można wykazać, że przewodniki z prądami
płynącymi w kierunkach przeciwnych odpychają się.
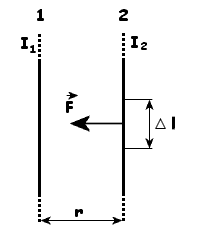
Obliczmy
siłę działającą na przewodnik, w którym płynie prąd
o natężeniu I2. Przewodniki są prostoliniowe
i nieskończenie długie, ale rozpatrujemy siłę działającą
na długości Δl.
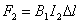
|
BF1 --> indukcja magnetyczna pola przewodnika
1 |
|
IF2 --> natężenie prądu w przewodniku 2 |
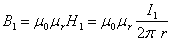
Po
podstawieniu otrzymamy:
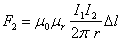
Pamiętajmy,
że µr dla przewodnika
znajdującego się w próżni wynosi 1.
Będąc
w tym miejscu tego wywodu, należałoby wspomnieć o
definicji ampera absolutnego .
Niech będą zatem dane dwa przewodniki prostoliniowe
nieskończenie długie z prądami o równych natężeniach
po 1A każdy, umieszczone w próżni w odległości 1m
od siebie. Obliczmy siłę działającą na przewodniki
na długości 1m .
Powyższe dane podstawiamy do wyprowadzonego powyżej
wzoru:
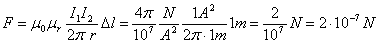
Na
podstawie powyższego zadania definiujemy wzorzec ampera
absolutnego, tj. jednej z podstawowych jednostek układu
SI. Jest to oczywiście jednostka natężenia prądu.
Amper
absolutny jest natężeniem prądu, który płynąc w dwóch
równoległych nieskończenie długich przewodnikach o
znikomym przekroju okrągłym, umieszczonych w próżni
w odległości 1m od siebie, powoduje oddziaływanie
wzajemne tych przewodników siłą 2.10 -7
N na każdy metr bieżący tych przewodników.
4.
Ruch ładunków w polu magnetycznym
Rozpatrywać
będziemy ruch cząstki naładowanej w jednorodnym polu
magnetycznym. Rodzaj ruchu i kształt toru zależeć
będą od prędkości początkowej, jaką nadaje się cząstce.
Ze względu na tę prędkość początkową rozróżnimy kilka
przypadków ruchu.
Przypadek
I
Ładunek
q umieszczono w polu magnetycznym, nie nadając mu
żadnej prędkości początkowej.
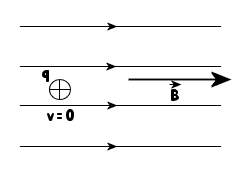
Na
ładunek w polu magnetycznym może działać siła Lorentza
( F=Bqvsinα), ale w naszym przypadku
ze względu na spoczynek ładunku, wartość tej siły
równa jest zeru.
Z
I zasady dynamiki wynika, że ładunek
w tym przypadku pozostaje w spoczynku.
Przypadek
II
Ładunkowi
q nadano prędkość początkową v o kierunku równoległym
do linii pola.
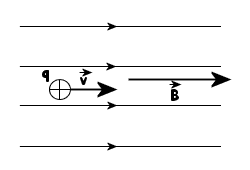
Na
ładunek może działać siła Lorentza ( F=Bqvsinα),
ale ponieważ kąt α=0 , czyli sinα=0
, zatem F=0 .
Zgodnie
z I zasadą dynamiki, ładunek w tym
przypadku porusza się ruchem jednostajnym prostoliniowym,
zachowując nadaną mu prędkość równoległą do linii
pola.
Przypadek
III
Ładunkowi
q nadaje się prędkość początkową o kierunku prostopadłym
do linii pola.
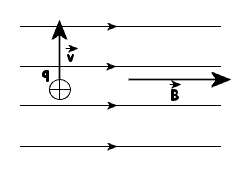
Na
ładunek działa siła Lorentza. W naszym przypadku α=90°
, a więc sinα=1. Siła Lorentza ma wartość
F=Bqv , a jej zwrot wyznaczony za pomocą reguły Fleminga
jest za rysunek. Dla lepszego przedstawienia wykonamy
rysunek tak, by linie pola były prostopadłe do płaszczyzny
rysunku (rysunek po prawo):
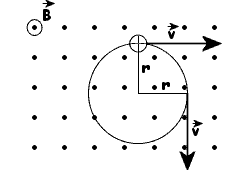
Siła Lorentza jest w każdym punkcie toru prostopadła
do wektora prędkości. Taka siła nie powoduje zmiany
wartości prędkości, lecz zakrzywia tor ruchu. Jest
więc siłą dośrodkową. Fakt, że siła Lorentza jest
siłą dośrodkową wyrazimy równością:
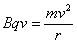
|
stąd:
|
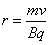
|
Ładunek
w tym przypadku porusza się ruchem jednostajnym po
okręgu o wyżej podanym promieniu, a okresie obliczonym
ze wzoru na prędkość liniową :
więcej
o ruchu jednostajnym po okręgu >
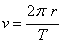
stąd
okres :
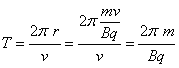
i
częstotliwość :
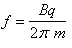
Przypadek
IV
Ładunkowi
q nadaje się prędkość początkową skierowaną pod kątem
0 < α < 90° do linii pola magnetycznego.
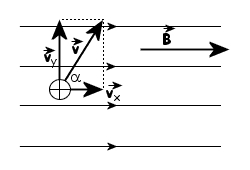
Prędkość
początkową rozkładamy na składowe: równoległą do linii
pola v x i prostopadłą do linii
pola v y . Gdyby ładunek posiadał
jedynie prędkość v x , poruszałby
się jak w przypadku II ruchem jednostajnym prostoliniowym,
równolegle do linii pola. Gdyby zaś ładunek miał jedynie
prędkość prostopadłą do linii pola v y ,
poruszałby się jak w przypadku III tj. ruchem jednostajnym
po okręgu. Ponieważ ładunek posiada obie prędkości
składowe, więc wykonuje oba wyżej wymienione ruchy
składowe jednocześnie.
Torem ruchu wypadkowego jest linia śrubowa (rysunek
po prawo).
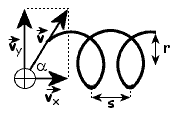
Promień
śruby r obliczamy jak w przypadku III:
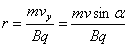
Okres
jednego obiegu T obliczamy również jak w przypadku
III:
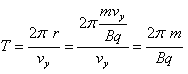
Skok
linii śrubowej s jest równy drodze przebytej przez
ładunek ruchem jednostajnym z prędkością v x
, wzdłuż linii pola, w czasie okresu T .
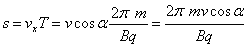
|