 Spadek
swobodny,
Rzuty Spadek
swobodny,
Rzuty
Spadek
swobodny
Jest to ruch jednostajnie przyśpieszony bez prędkości
początkowej z przyśpieszeniem ziemskim g.

Rys. 1 |
Rys. 2 |
Prędkość ciała po określonym czasie wyraża wzór
v=gt, drogę jaką przebywa ciało wzór: h=gt2/2,
a odległość od początku układu (właściwie początku
osi Y tego układu, oś X nas nie interesuje bo
ruch zachodzi w pionie)
y(t)=h1-gt2/2 |
Rzut pionowy w górę
Rzut pionowy w górę jest ruchem jednostajnie opóźnionym
z prędkością początkową v0, opóźnienie w
tym ruchu wynosi g=9,81m/s2- przyśpieszenie
ziemskie. Wysokość jaką ciało osiąga wyraża wzór h=v0t-gt2/2,
a prędkość po określonym czasie wzór vk=v0-gt
(vk-prędkość końcowa, v0- prędkość
początkowa. Wykorzystując oba te wzory jesteśmy w stanie
wyprowadzić wzór na maksymalną wysokość na jaką wzniesie
się ciało. I tak wiedząc, że na maksymalnej wysokości
ciało będzie miało prędkość końcową równą 0, to:
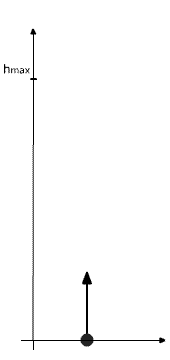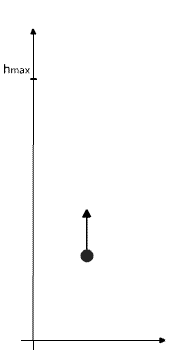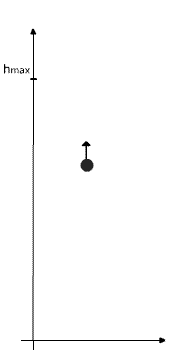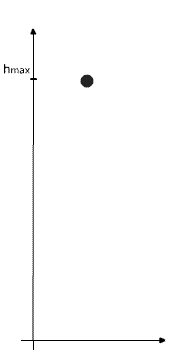 |
vk=v0-gt
0=v0-gt /po przekształceniu/
t=v0/g
Skoro w tym czasie ciało osiągnie prędkość
równa zero to w tym czasie osiągnie ono maksymalną
wysokość. Dlatego podstawiając powyższy wzór
na czas w miejsce t we wzorze na wysokość, jaką
ciało osiąga, otrzymamy wzór na wysokość maksymalną.
hmax=v0t - gt2/2
hmax=v0(v0/g)
- g(v0/g)2/2
hmax=v02/g
- v02/2g
hmax=2v02/2g
- v02/2g
Otrzymujemy wzór końcowy na wysokość maksymalną
ciała w rzucie pionowym w górę:
 |
Rzut pionowy w dół
Rzut pionowy w górę jest ruchem jednostajnie przyśpieszonym
z prędkością początkową- v0, ruch odbywa
się jak sama nazwa wskazuje w pionie,a przyśpieszeniem
jest przyśpieszenie ziemskie g. Prędkość po określonym
czasie wyraża wzór vk=v0+gt, natomiast
wzór na drogę przebytą przez ciało (w pionie) oraz odległość
od początku układu (np. powierzchni Ziemi) zależy od
wybranego przez nas układu odniesienia. Zajmijmy się
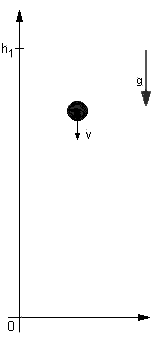
najpierw układem przedstawionym na rys. 1.
| Ciało
znajduje się w początku osi Y (czyli pionowej
osi). Czerwony wektor wskazuje kierunek działania
przyśpieszenia ziemskiego g=9,81m/s2.
Odległość od początku układu jest równa drodzę
jaką to ciało przebywa (y(t)=h) i opisuje je wzór:
h=v0t+at2/2.
Przejdźmy teraz do drugiego układu (rys. 2),w
którym ciało znajduje się względem niego na
wysokości h1, wzór na drogę jaką
pokonuje ciało to: h=v0t+at2/2,
a odległość od początku układu (dokładniej początku
osi Y, bo tylko ona nas interesuje w tym ruchu)
y(t)=h1-v0t-at2/2
|
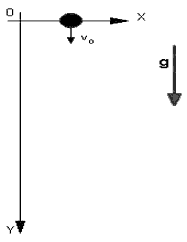
rys. 1 |
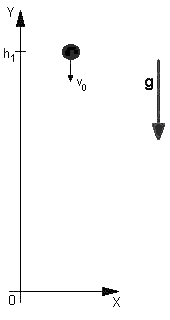
rys. 2 |
Rzut poziomy
Rzut poziomy jest ruchem, który traktujemy jako złożenie
dwóch ruchów (podobnie jak rzut ukośny):
- w pionie-
ruch jednostajnie przyśpieszony z prędkością początkową
równą 0 (ponieważ na początku ruchu jest tylko składowa
v0 działająca w poziomie!), czyli spadek
swobodny.
- w poziomie-
ruch jednostajny, w którym prędkość (składowa v1)
jest w każdej chwili równa prędkości początkowej
v0
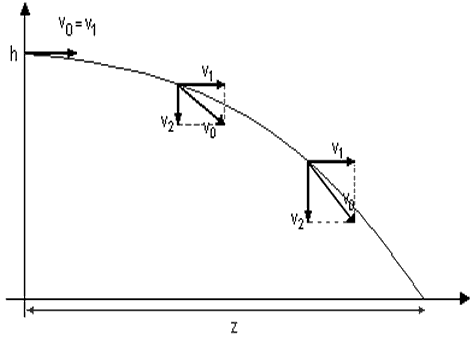
Zajmijmy się najpierw ruchem jaki zachodzi w pionie
(składowa v2), jak wcześniej wspomniałem
jest to spadek swobodny (ruch jednostajnie przyśpieszony
z przyśpieszeniem ziemskim g=9,81m/s), a więc prędkość
początkowa w tym ruchu jest równa 0, dlatego znając
wysokość z jakiej rzucono ciało, na podstawie wzoru
h=gt2/2, możemy wyznaczyć czas, po którym
ciało spadnie na ziemię:
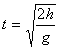
A skoro w tym czasie ciało spadnie na ziemię to w tym
czasie osiągnie również maksymalną odległość- zasięg
rzutu. Jeżeli w poziomie odbywa się ruch jednostajny,
ze stałą prędkością równą wartości prędkości początkowej
(v0=v1) to wykorzystując wzór
na drogę w tym ruchu s=vt i za czas podstawiając wcześniej
przekształcony wzór, otrzymujemy wzór na zasięg rzutu
poziomego (v=v0):

W każdej chwili jesteśmy w stanie obliczyć odległość
od początku układu odniesienia, prędkość ciała oraz
przyśpieszenie, i tak:
- r=[v0;h-gt2/2]
- v=[v0;gt]
- a=[0;g]
Jesteśmy także w stanie wyznaczyć wartość prędkości
v0 w każdym momencie ruchu.(rys. 2)
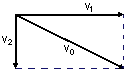 rys. 2 rys. 2
Aby to zrobić zastosujemy twierdzenie Pitagorasa:
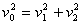
Po przekształceniach otrzymujemy:
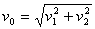
Jak wiemy prędkość v2 możemy wyliczyć ze
wzoru v2=v2p+gt (v2-
wartość prędkości po czasie t, v2p- wartość
składowej v2 na początku ruchu, czyli 0.
I tak v2=gt, podstawiając do wcześniejszego
wzoru otrzymujemy:
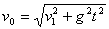
A podstawiając w miejsce czasu wcześniej wyliczony wzór
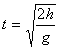 , otrzymamy: , otrzymamy:
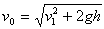
Rzut ukośny
Z rzutem ukośnym spotykamy się rzucając kamieniem, czy
kopiąc piłkę. Traktujemy go jako złożenie dwóch ruchów:
- jednostajnego- w poziomie
- jednostajnie opóźnionego (rzut pionowy)- w pionie
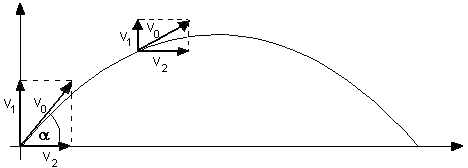
Wektor v0 jest wektorem wypadkowym wektora
v1 oraz v2. W poziomie odbywa
się ruch jednostajny, prędkość w tym ruchu jest stała
w każdej sekundzie tego ruchu i jest wyrażona wzorem
v2=s/t, natomiast w pionie ruch jednostajnie
opóźniony z prędkością początkową v1 i
z opóźnieniem g (przyśpieszenie ziemskie) równym w
przybliżeniu 9,81m/s2, czyli po prostu
jest to rzut pionowy, prędkość ciała w tym ruchu wyraża
wzór vk=v1-gt, gdzie vk-
jest prędkością końcową, t- to czas. Drogę (w pionie)
jaką przebywa to ciało wzór h=v1t-gt2/2.
Tak, więc możemy w każdej chwili obliczyć położenie,
prędkość oraz przyśpieszenie ciała stosując równania,
utworzone z powyższych wzorów:
- przemieszczenie
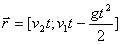
- prędkość
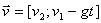
- przyśpieszenie
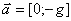
Jeżeli
dysponujemy wartością kąta, pod jakim rzucono ciało
oraz prędkością v0, możemy obliczyć prędkości
składowe, stosując funkcje trygonometryczne:
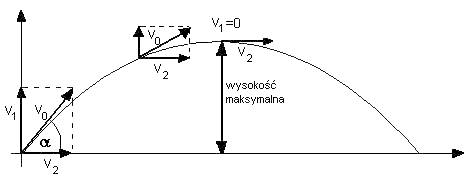
Przyjrzyjmy się teraz momentowi, gdy ciało osiąga maksymalną
wysokość jak widać na powyższym rysunku prędkość v1
osiągnęła wartość 0. Wyprowadźmy teraz wzór, dzięki
któremu obliczymy maksymalną wysokość, na jaką wzniesie
się ciało w rzucie ukośnym, aby to zrobić należy zająć
się ruchem w pionie, czyli rzutem pionowym (składowa
v1), nie interesuje nas ruch poziomy (składowa
v2). Wzór na prędkość końcową w rzucie pionowym
to: vk= v1- gt wiemy, że w chwili
osiągnięcia maksymalnej wysokości, wartość składowej
v1=0, a więc: 0= v1- gt po przekształceniu
wzoru otrzymujemy: t=v1/g jest to czas, po
którym ciało osiągnie maksymalną wysokość. Następnie
wzór na wysokość w rzucie pionowym: h=v1t-gt2/2,
za t podstawiamy wcześniej otrzymany wzór na czas, po
którym ciało osiągnie maksymalną wysokość, dzięki czemu
obliczana przez nas wysokość będzie wysokością maksymalną,
na jaką wzniesie się ciało. I tak, po przekształceniach,
otrzymujemy:
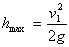
jednak wzór na wysokość maksymalną, w którym musielibyśmy
znać składową v1 jest niewygodny, najczęściej
w zadaniach dysponujemy prędkością v0 oraz
kątem pod jakim rzucono ciało, dlatego w miejsce v1
wstawiamy wzór: v0 sina=v1
, który jest przekształceniem już wcześniej wymienianego
wzoru, dzięki temu otrzymujemy:
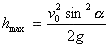
Zajmijmy się teraz wyprowadzeniem wzoru na zasięg rzutu
ukośnego. Pomoże nam w tym poniższy rysunek:
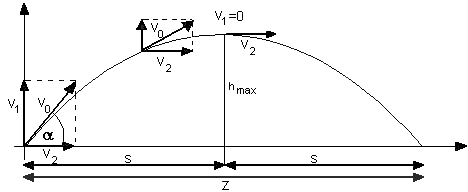
Wiemy, że czas wznoszenia się
ciała na maksymalną wysokość jest taki sam jak czas
opadania i zgodnie z obliczeniami, które wcześniej wykonaliśmy
wyraża go wzór t=v1/g, skoro tak to w tym
czasie ciało pokonało połowę maksymalnej drogi w poziomie
(s), która jest obliczana ze wzoru s=v2 t,
a t wynosi v1/g, czyli:
s=v2v1/g
Zasięg rzutu (z) składa się z dwóch odcinków s, skoro
tak to:
z=2v2v1/g
Ale taka forma wzoru na zasięg,
w której występują prędkości składowe nie jest wygodna
w użyciu, ponieważ, tak jak w przypadku wysokości maksymalnej
zazwyczaj dysponujemy prędkością v0 i kątem,
pod którym rzucono ciało, dlatego wykorzystamy równości
v1= v0 sina
oraz v0= v2 cosa
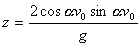 po przekształceniu otrzymujemy
właściwy wzór: po przekształceniu otrzymujemy
właściwy wzór:
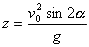
|