Równia pochyła, siła tarcia

Siła tarcia jest siłą bierną, tzn, że pojawia się, kiedy na stykające się ciała zaczynają działać siły równoległe do podłoża. Rozważmy przypadek, w którym przesuwamy szafę (rys.1).
Q - ciężar ciała, równy naciskowi (N), bo ciało jest na płaskiej powierzchni,
F_r - siła reakcji podłoża.

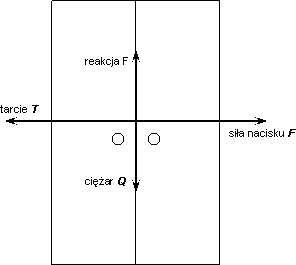
rys.1

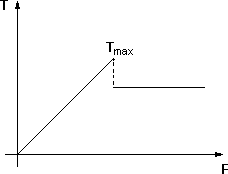
(rys.2)

Odcinek nachylony - tarcie statyczne, odcinek równoległy do osi F - tarcie dynamiczne

Człowiek działa na szafę taką siłą F, że pod jej wpływem szafa się nie przesuwa. Dzieje się tak, ponieważ w chwili, kiedy człowiek przyłożył siłę F pojawiła się siła tarcia T równa, co do wartości sile F, lecz zawsze przeciwnie skierowaną do jej zwrotu F = T. Załóżmy, że człowiek zwiększa przyłożoną do szafy siłę F (ale tak, że szafa wciąż pozostaje w spoczynku), wtedy siła tarcia także wzrasta i wciąż będzie spełniona równość F = T. Siłę tarcia, która działa na ciało nie będące w ruchu nazywamy tarciem statycznym lub spoczynkowym. A teraz przyjrzyjmy się momentowi, w którym człowiek przyłożył taką siłę, że ciało zaczęło się przemieszczać. Siła tarcia statycznego osiągnęła w tym momencie maksymalną wartość, po czym siła tarcia uległa zmniejszeniu - ta siła to tarcie dynamiczne lub poślizgowe, do którego wrócimy później. Na wykresie (rys.2) pokazano jak zmienia się wartość siły tarcia T w zależności od przyłożonej siły F.

Siła tarcia statycznego zależy od rodzaju podłoża (a właściwie rodzaju stykających się powierzchni) oraz siły nacisku (na równym podłożu jest równa ciężarowi, N = Q, inaczej rzecz się przedstawia na równi pochyłej). Wzór na maksymalne tarcie statyczne, czyli wartość siły tarcia, po której przekroczeniu ciało ruszy z miejsca to:

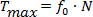
gdzie 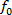 - współczynnik tarcia statycznego.

Kiedy siła F przekroczy wartość T₀max to ruchowi ciała przeciwdziała zawsze mniejsze tarcie posiadające stałą wartość, bez względu na prędkość ciała- tarcie poślizgowe (dynamiczne). Wzór wyrażający jego wartość jest podobny do wzoru na tarcie statyczne:

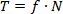
ale f - jest współczynnikiem tarcia dynamicznego, zazwyczaj jest mniejszy niż współczynnik tarcia statycznego.

Równia pochyła

Rozważmy jakie siły towarzyszą ciału znajdującemu się na równi pochyłej o wysokości h, długości równi l, długości podstawy x i kącie nachylenia , kiedy ciało zacznie się zsuwać i dlaczego.

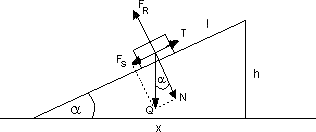
Ciało znajdujące się na równi pochyłej działa siłą ciężkości Q, której wektor skierowany jest prostopadle do podłoża.

Rozłóżmy wektor siły Q na składowe:
- siła nacisku N, skierowana zawsze prostopadle do powierzchni równi
- siła powodująca zsuwanie ciała F_s, której wektor jest równoległy do powierzchni równi

Ponadto występują jeszcze siły F_R - siła reakcji podłoża, która równoważy siłę nacisku N oraz siła tarcia, przeciwnie skierowana do siły F_s i równa jej jeżeli ciało nie zsuwa się z równi.

Kąt, jaki tworzy ze sobą siła nacisku N i ciężar Q jest zawsze taki sam jak kąt nachylenia równi (ponieważ trójkąt xhl jest podobny do trójkąta NF_sQ), więc dysponując ciężarem i kątem nachylenia równi pochyłej możemy wyliczyć każdą siłę. I tak:

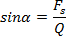
Czyli

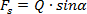
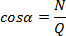
Czyli

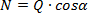
Ponadto prawdziwe są proporcje:

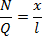
z twierdzenia Pitagorasa

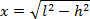
Więc

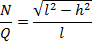
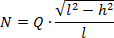
oraz

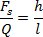
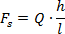
Pozostaje nam jeszcze jedna siła - siła tarcia. Jeżeli ciało na równi pozostaje w spoczynku to siła tarcia jest równa sile zsuwania. Dzięki temu za pomocą równi możemy obliczać współczynniki tarcia statycznego. Aby to zrobić należy umieścić ciało na równi o jak największym kącie nachylenia, przy czym ciało nie może się przemieszczać! Wtedy F_s =T max (T_max -maksymalna wartość tarcia statycznego), wiemy też, że:
T_max = f₀ N,

więc:

F_s = f₀ N,

i tak otrzymujemy

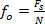
Korzystając z wcześniej wyprowadzonych wzorów otrzymujemy:

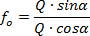
co po przekształceniu daje:
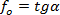