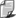Energia, czyli paliwo wszelkich przemian

Pojęcie energii jest fundamentalne dla całej fizyki. Właściwie trudno jest wymyślić inną wielkość o podobnie dużym znaczeniu. Łączy ona ze sobą różne zjawiska i procesy - jest jakby wspólnym mianownikiem pozwalającym porównywać ze sobą przemiany chemiczne, cieplne, elektryczne, promieniowanie, ruch dużych obiektów, grawitację i rozpady cząstek elementarnych. Inną bardzo użyteczną cechą energii jest to, że choć w wielu sytuacjach nie sposób jest dokładnie określić, jakie siły wpływają na zachowanie się obiektów, to podejście energetyczne umożliwia "obsługę" matematyczną tych zjawisk. Wszystko to razem sprawia, że w dzisiejszej fizyce bez zrozumienia zagadnienia energii trudno wyjść poza zakres szkoły podstawowej.

Praca! Wielkość pozwalająca definiować różne postaci energii.
Jako podstawę do wprowadzenia pojęcia energii przyjmuje się zazwyczaj wielkość zwaną pracą. Zdefiniowana jest ona tak:

Praca = Siła ^. Przesunięcie

Co można zapisać wzorem literowym

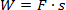
Znaczenie symboli:

F - siła,
s - przesunięcie,
W - praca

Przy czym, ponieważ niekiedy się zdarza, że siła działa w innym kierunku niż odbywa się przesunięcie, więc przyjęło się uściślić powyższy wzór do postaci:

Praca = Siła ^. Przesunięcie_{w kierunku siły}

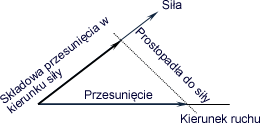
lub, w całkowicie równoważnym ujęciu:

Praca = Siła_{w kierunku przesunięcia} ^. Przesunięcie

Pamiętajmy, że trzeba zawsze wziąć te składowe wektory siły, lub przesunięcia, które są zgodne z kierunkiem drugiego wektora.
Praca jest wielkością skalarną. Oznacza się ją najczęściej literą W (z angielskiego Work), rzadziej z łaciny L (Labor). Jednostką pracy jest dżul (J), od nazwiska fizyka brytyjskiego Jamesa Joula.

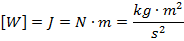
Wartość pracy, z uwzględnieniem kąta między siłą i przesunięciem, można też obliczyć ze wzoru:

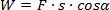
Wzór ten jest prostym zastąpieniem składowej siły w kierunku przesunięcia za pomocą wartości siły i kosinusa kąta (lub odpowiednio składowej przesunięcia zgodnej z kierunkiem siły). Minimalna znajomość trygonometrii pozwala na samodzielne wyprowadzenie ostatniego wzoru z definicji pracy określonych wyżej.

Związek pracy z energią

To, że pracę, a później energię, wylicza się poprzez przemnożenie wartości siły i przesunięcia, nie jest przypadkiem. Postaram się uzasadnić, że tego typu wielkość najlepiej łączy się z tym, co intuicyjnie rozumiemy przez energię - czyli wielkość odpowiadającą za wykonywanie zmian w otoczeniu.
Aby dobrze zrozumieć ten fakt, zastanówmy się najpierw, co mogłoby dobrze odpowiadać typowemu wyobrażeniu energii. Można dość wyraźnie związać tę wielkość z elektrownią wodną i masami wody zgromadzonymi na pewnej wysokości. Woda, spadając z wysokości kilku, kilkunastu, czy kilkudziesięciu metrów, uderza o łopatki koła lub turbiny, co umożliwia wyprodukowanie energii elektrycznej, zmielenie ziarna we młynie, czy też wykonanie innej użytecznej pracy. Dlatego można powiedzieć, że w masach wody zalegających na wysokości większej niż znajduje się maszyna do jej przetwarzania, jest zawarta energia. Energii też potrzeba, aby tę wodę na górę dostarczyć, a w wybranym przez nas czasie można tę energię odebrać (w oparciu o powyższą zasadę działają elektrownie szczytowo - pompowe).

Zastanówmy się teraz, jakie parametry wody wpływają na ilość zgromadzonej przez wodę energii. Myślę, że dość szybko dojdziemy do wniosku, że kluczowe są tu dwie podstawowe wielkości:

• ilość spadającej wody, lub dokładniej jej ciężar (im więcej ciężkiej wody spada, tym więcej energii)
• wysokość z jakiej spada woda (spadek z 1 m niewielkie ma szanse napędzić duże urządzenie w porównaniu z taką samą ilością wody spadającą np. z 10 m).

Dlatego energia zgromadzona w masach wody jest iloczynem:

• siły ciężkości F (ciężar ciała jest równy sile ciężkości)
• wysokości spadku S

Mnożąc te wielkości przez siebie otrzymujemy właśnie definicję pracy - siła razy przesunięcie:

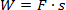
Pracę wody z elektrowni można rozumieć na dwa sposoby:

• jest to praca, jaką oddaje nam woda spadając z wysokości S ,
• lub praca, którą trzeba włożyć w wyniesienie jej na wysokość S

Dokładna równość tych dwóch rodzajów pracy zachodzi dopiero po odliczeniu ubytków energii związanych z pokonywaniem sił tarcia.

Energia potencjalna

Ostatecznie, po zaniedbaniu nieistotnych w tej chwili czynników, można przyjąć, że praca włożona w wyniesienie wody jest równa pracy, jaką można odzyskać dzięki uderzeniom wody o łopatki młyna. Dlatego mówimy, że woda zgromadzona na pewnej wysokości posiada energię potencjalną ciężkości. Słowo potencjalna oznacza tu to, że jest ona związana z położeniem i oddziaływaniem, czyli jest jakby energią statyczną - niezwiązaną z ruchem. Rodzajów energii potencjalnej jest kilka, a różnią się one typem oddziaływania, z którym są związane. Oprócz energii potencjalnej ciężkości mamy jeszcze: energię potencjalną sprężystości (związaną z oddziaływaniami sprężystymi) oraz energię potencjalną elektrostatyczną (m.in. działającą na cząstki naładowane poruszające się w polu elektrycznym). Ogólnie, cechą charakterystyczną energii potencjalnej jest to, że jest ona przypisana do położenia ciała, np. bliżej źródła oddziaływania może być większa.
Najprostszą postać energii potencjalnej otrzymujemy dla energii potencjalnej ciężkości ciał znajdujących się przy powierzchni ziemi. Wtedy wyraża się ona wzorem:

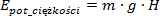
Tutaj:
m - masa ciała,
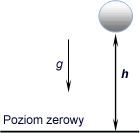
g - przyspieszenie ziemskie,
h - wysokość ponad poziom odniesienia na którym energia jest równa zero.

Energia kinetyczna
Inną, niezwykle ważną postacią energii jest energia kinetyczna. Jej nazwa pochodzi od greckiego terminu "kineo" (ruch) i słusznie sugeruje, że jest ona związana z ruchem ciała. Wartość energii kinetycznej jest równa pracy, jaką trzeba włożyć, aby rozpędzić ciało. Po wykonaniu tej pracy rozpędzone ciało będzie posiadało energię ruchu - "zgromadzoną" pracę rozpędzania. Energię tę można z kolei wykorzystać na wykonanie zmian w otoczeniu - np. rozpędzona kula kamienna wystrzelona ze średniowiecznego działa może zburzyć mur, kula tocząca się po torze rozrzuca kręgle, rozpędzona woda porusza łopatki turbiny itp. W większości typowych przypadków odzyskanie, omawianej w poprzednim rozdziale, energii potencjalnej odbywa się za pośrednictwem energii kinetycznej.

Energię kinetyczną obliczamy ze wzoru:

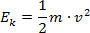
Znaczenie symboli:
v - prędkość ciała
m - masa ciała

Teraz krótkie odpowiedzi na narzucające się pytania o energii kinetycznej:

Od czego zależy energia kinetyczna?

Oczywiście od prędkości i masy ciała. Jednak nie jest ona prostym iloczynem tych wielkości - prędkość "znaczy" tu więcej, bo jest podniesiona do kwadratu.

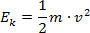
Trzeba przy tym dodać, że energia kinetyczna zależy od układu odniesienia - w jednym układzie może być inna niż w drugim.

Dlaczego energia kinetyczna rośnie bardziej ze wzrostem prędkości niż masy?

- wynika to z faktu, że praca związana z rozpędzaniem ciała o kolejny metr na sekundę jest większa dla ciał poruszających się szybko, niż dla tych wolnych. Tak musi być, bo praca, to siła razy droga, a przy szybkim ruchu i tej samej sile, droga ta będzie większa. Fakt ten łatwo jest "poczuć" kierując samochodem - gdy chcemy wyprzedzać przy dużej prędkości wtedy moc silnika nie wystarcza już na tak sprawne przyspieszanie, jak przy małych prędkościach.

Czy powyższy wzór na energię kinetyczną jest ścisły?

Pewne odchylenia od powyższego wzoru mogą pojawić się dla ciał poruszających się z ogromnymi prędkościami (bliskimi prędkości światła). Efekt ten (nazywany efektem relatywistycznym) związany jest z teorią względności Einsteina. Na szczęście można przyjąć, że dla typowych, (a nawet w zwykłym pojęciu dużych) prędkości wzór jest bardzo dokładny - np. dla rakiety poruszającej się z pierwszą prędkością kosmiczną poprawka relatywistyczna jest tak mała, że nie mieści się na moim kalkulatorze - jest poniżej jednej miliardowej.

Energia sprężystości

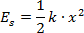
Energia sprężystości zgromadzona w rozciągniętej sprężynie zależy od: wielkości rozciągnięcia (czyli przesunięcia końca sprężyny) - x stałej sprężystości sprężyny - k, (czyli wielkości określającej jak dużej siły potrzeba, aby rozciągnąć sprężynę) Wzór, który łączy te wielkości w poprawną energię sprężystości ma postać Znaczenie symboli - jak wyżej.

Widać, że energia sprężystości silniej rośnie wraz z wielkością odkształcenia sprężyny, niż współczynnika sprężystości.

Trzeba jednak pamiętać, że wzór powyższy jest tylko przybliżeniem sprawdzającym się dla niezbyt dużych rozciągnięć x. Przy bardzo silnym rozciągnięciu sprężyna ulegnie rozprostowaniu i podana zależność w ogóle nie będzie miała zastosowania. Odchylenia od niej występują z resztą już dla nie tak ekstremalnych rozciągnięć. Ogólnie obowiązuje zasada, że im mniejsze rozciągnięcie, tym lepsza stosowalność wzoru na energię sprężystości.

Wzór powyższy obowiązuje nie tylko dla rozciągania, ale i dla ściskania, odchylania i uginania i ogólnie dla różnych odkształceń od położenia równowagi.

Zasada zachowania energii

To, że energia jest tak ważną wielkością wynika z jednego podstawowego faktu - obowiązuje zasada zachowania energii.
Postarajmy się więc zrozumieć istotę tego fundamentalnego prawa przyrody. Oto jego treść:

Sformułowanie 1:
W dowolnym procesie całkowita energia układu izolowanego jest stała.

Sformułowanie 2:
Całkowita energia izolowanego układu jest taka sama przed, jak i po wystąpieniu przemian w tym układzie.

Sformułowanie 3:
Zwiększyć energię izolowanego układu można tylko poprzez dostarczenie energii z zewnątrz, zmniejszenie energii tegoż układu może nastąpić tylko w wyniku wyemitowania jej poza układ.

Sformułowanie 4:
Energia nie ginie, ani nie powstaje samorzutnie.

Sformułowanie 5 (wzorem):

E_{układu izolowanego} = const

lub

lub

E_{postac1 k} + E_{postac2 k} + E_{postac3 k} + ... = E_{postac1 p} + E_{postac2 p} + E_{postac3 p} + ...

Tutaj poszczególne składniki energii sumują się ostatecznie do tej samej wartości.

Układ izolowany, jest to taki układ (zestaw ciał, obiektów), który nie kontaktuje się z innymi układami (obiektami). Prawdę mówiąc do obowiązywania zasady zachowania energii całkowita izolacja układu nie jest nawet konieczna. Wystarczy tylko, jeżeli tenże układ nie wymienia energii z otoczeniem.

Teraz wyjaśnimy co z powyższych sformułowań wynika.

Załóżmy, że rozpatrywany przez nas układ posiada tylko dwa rodzaje energii: energię kinetyczną i potencjalną.

Wtedy, z faktu, że wzrosła energia kinetyczna, możemy od razu wywnioskować o zmaleniu energii potencjalnej, ponieważ ich suma musi być stała. I w ten sposób zazwyczaj stosuje się w zadaniach zasadę zachowania energii - jeśli znamy całkowitą energią w pewnym momencie, a następnie tylko jeden ze składników w innym momencie, to możemy obliczyć wartość tego brakującego składnika.

Wyprowadzenie wzoru na energię kinetyczną

Wzór

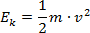
można wyprowadzić ze wzoru na pracę:

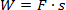
W tym celu zamiast siły F trzeba podstawić siłę związaną z popychaniem ciała podczas rozpędzania go, a zamiast drogi S - drogę rozpędzania.

Zróbmy to:

F = m ^. a

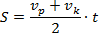
Jeśli zamiast przyspieszenia a zastosujemy jego definicję:

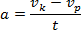
to siła przedstawi nam się w postaci:

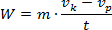
Teraz oba wzory (na drogę i na siłę umieścimy w definicji pracy):

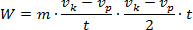
Skracamy czas i wobec iloczynu liczników stosujemy wzór skróconego mnożenia:
(a + b) ^. (a - b) = a₂ + b₂

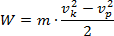
Jest do wzór na zmianę energii kinetycznej. Żeby dostać poszukiwaną przez nas postać zależności na samą energię kinetyczną musimy założyć, że początkowo ciało nie porusza się, czyli v_p = 0; zmienimy też oznaczenia: v_k oznaczymy po prostu, jako v. Wtedy otrzymamy wreszcie:

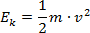
Udowodnienie, że podczas spadku swobodnego energia mechaniczna jest stała

Jest to szczególny przypadek zasady zachowania energii.

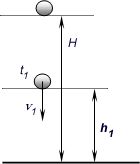
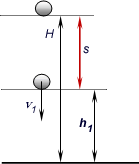
Sytuacja początkowa przedstawia się tak:

Ciało rzucamy z wysokości H. Obliczamy, jaką prędkość v1 będzie ono miało po pewnym czasie t 1 na wysokości h1. Zaniedbujemy opór powietrza. Potem dla punktu początkowego i końcowego obliczymy energię mechaniczną ze wzoru Emech = Ekin + Epot Dokładniej, po podstawieniu obu energii będziemy mieli:
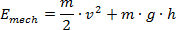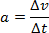
Zaczynamy! Najpierw wzory: Ponieważ ruch jest przyspieszony, to prędkość będziemy obliczać z definicji przyspieszenia: przy czym, ponieważ Dv = vk - vp to vk = vp + a . t Zamiast a trzeba podstawić wartość przyspieszenia ziemskiego g. Dlatego ostatecznie wzór na prędkość przyjmie postać: vk = vp + g . t Teraz tylko uściślenie nazw: nasz czas, i prędkość końcowa, to t1 i v1, prędkość początkowa (ta na samej górze) jest równa zero. Dlatego: v1 = g . 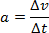t1	Wzory ogólne potrzebne w tym zadaniu: definicja przyspieszenia: Wzór na drogę w ruchu jednostajnie przyspieszonym: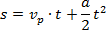
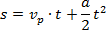
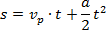
Przyjrzyjmy się jak wygląda sytuacja, jeśli chodzi o drogę: Przebyta przez ciało droga oznaczona tu jest przez s (na niebiesko). Widać z rysunku, że h1 = H - s Z drugiej strony s można obliczyć ze wzoru na drogę w ruchu przyspieszonym: Wzór się uprości po uwzględnieniu, że vp = 0. Przy okazji podstawimy też a = g i t = t1 (to zmiana oznaczeń). Czyli mamy: a więc
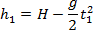Obliczmy wreszcie energię całkowitą mechaniczną, ze wzoru:
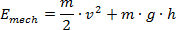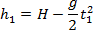
Energia mechaniczna niżej. Wysokość: Czas: t = t1 Prędkość: v = v1 = g  . t1	Energia mechaniczna na górze wysokość: h = H Czas: t = 0 Prędkość początkowa v = 0
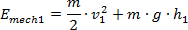
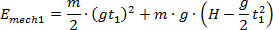
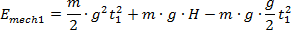
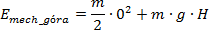
po zlikwidowaniu nawiasów otrzymamy: Składniki pierwszy i trzeci redukują się i otrzymamy: Emech1 = m . g . H	czyli Emech gora = m . g . H

Porównanie wyników uprawnia nas do sformułowania wniosku:

Bez względu na wybór chwili czasu t (uwaga, że t jest tu zmienną, czyli może przybierać dowolne wartości), otrzymujemy zawsze taki sam wzór na energię mechaniczną:

E_mech = m ^. g ^. H

Czyli inaczej:

Energia mechaniczna jest taka sama w każdym momencie spadku swobodnego. Udowodniliśmy dla tego przypadku zachowanie energii mechanicznej.

Wyprowadzenie wzoru na pracę podnoszenia ciała (energię potencjalną ciężkości)

Załóżmy, że chcemy ciało o masie m podnieść na wysokość H. Obliczymy pracę jaka jest do tego potrzebna
(wzór na pracę ).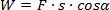

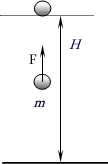
Musimy użyć do tego siły F. Jak dużej?

Na pewno nie mniejszej niż ciężar ciała: P = m ^. g.

Ale czy dużo większej?

Wcale nie! Wystarczy tylko na początku minimalnie większa siła, a potem nadaną ciału prędkość wystarczy tylko utrzymywać stałą siłą

F = P

Dlatego do naszego wzoru na pracę podstawimy:

F = P = m ^. g

Skonfrontujmy to z naszym celem ostatecznym, czyli wzorem na pracę:

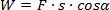
Mamy już pierwszy wyraz w tym iloczynie. Teraz o dwóch pozostałych:

s - droga. Tutaj oczywiście mamy do przebycia wysokość H. Zatem

s = H

No i ostatnia sprawa: cos a. Tutaj po prostu dla uproszczenia założymy, że podnosimy ciało pionowo do góry (ten sam wynik otrzymamy również bez tego założenia, ale przekształcenie byłyby bardziej skomplikowane). W takim przypadku kierunek ruchu jest taki sam jak kierunek działającej siły i kąt 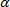= 0. A ponieważ cos0° = 1, to praca nam się uprości do wzoru:

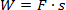
Podstawmy teraz siłę i drogę:

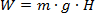
I to jest wynik!

Ta praca jest jednocześnie równa energii potencjalnej ciężkości jaką ma ciało znajdujące się na wysokości H .
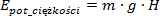