 Przyspieszenie, czyli jak szybko zmienia się prędkość
Przyspieszenie, czyli jak szybko zmienia się prędkość
Ruch jednostajny, jaki opisywany był w poprzednim przedziale nie jest zbyt częstym przypadkiem, zazwyczaj, prędzej czy później, prędkość ulegnie zmianom. Do opisywania zmian prędkości używana jest wielkość zwana przyspieszeniem. Przyspieszenie jest wielkością mówiącą nam o tym jak szybko zmienia się prędkość. Np. jeżeli prędkość nie zmienia się, wtedy przyspieszenie ciała jest równe zero. Jeżeli zaś w ciągu sekundy prędkość rośnie o 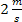 , wtedy przyspieszenie tego ruchu ma wartość , wtedy przyspieszenie tego ruchu ma wartość 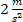 . .
Przyspieszenie jest wielkością informującą o tym jak szybko zmienia się prędkość ciała.
Np. jeżeli przyspieszenie ciała wynosi 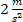 , to znaczy, że w ciągu 1s prędkość przyrasta o , to znaczy, że w ciągu 1s prędkość przyrasta o 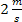 . .
Definicja przyspieszenia
Znaczenie symboli:
| symbol |
nazwa wielkości |
rodowód symbolu |
jednostka wielkości |
 |
przyspieszenie |
z ang. acceleration - przyspieszenie |
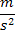 |
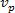 |
prędkość początkowa |
ang. velocity - prędkość |
 |
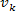 |
prędkość końcowa |
ang. velocity - prędkość |
 |
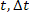 |
czas (z ang. time), w jakim prędkość zmieniła się od V p do V k |
z ang. time - czas |
s |
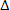 |
różnica prędkości końcowej i początkowej |
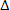 symbol delta (litera alfabetu greckiego) oznacza zazwyczaj przyrost jakiejś wielkości symbol delta (litera alfabetu greckiego) oznacza zazwyczaj przyrost jakiejś wielkości |
 |
Przykłady użycia definicji przyspieszenia:
1. Jeżeli prędkość ciała wzrosła od prędkości 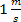 do prędkość do prędkość 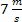 w ciągu 2 sekund, to średnie przyspieszenie ciała wyniosło: w ciągu 2 sekund, to średnie przyspieszenie ciała wyniosło:
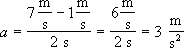
2. Przyspieszenie ciała wynosi 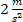 . O ile metrów na sekundę wzrośnie w tym ruchu prędkość ciała? . O ile metrów na sekundę wzrośnie w tym ruchu prędkość ciała?
Wzór definiujący przyspieszenie
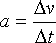
mnożymy obustronnie przez 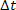 . Otrzymamy wtedy: . Otrzymamy wtedy: |
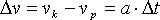 |
| Podstawiamy dane liczbowe: |
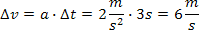 |
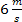 - ten wynik nie jest specjalnie ciekawy..., ale to tylko taki przykład ćwiczebny. - ten wynik nie jest specjalnie ciekawy..., ale to tylko taki przykład ćwiczebny. |
|
3. Jeżeli początkowa prędkość ciała wynosi 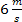 , a przyspieszenie , a przyspieszenie 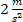 , to jaka będzie prędkość ciała po 3 sekundach ruchu? , to jaka będzie prędkość ciała po 3 sekundach ruchu?
| W poprzednim zadaniu pojawił się wzór: |
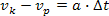 |
| Jeśli dodamy do obu jego stron v p otrzymamy: |
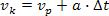 |
| A stąd już tylko krok do wyniku liczbowego |
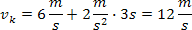 |
Wektor przyspieszenia
Wektor przyspieszenia możemy wyobrażać sobie jako strzałkę, która pokazuje o ile wydłuży się (lub skróci) wektor prędkości po jednej sekundzie .
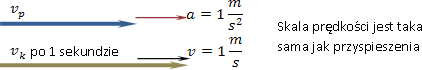
Ten model rysunkowy jest słuszny, gdy skala prędkości 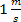 na rysunku jest taka sama jak skala przyspieszenia 1m/s2 . na rysunku jest taka sama jak skala przyspieszenia 1m/s2 .
W zależności od kierunku i zwrotu wektora przyspieszenia w stosunku do wektora prędkości możemy wyróżnić trzy sytuacje:
Gdy |
wtedy |
i mamy |
| wektor przyspieszenia jest skierowany zgodnie ze zwrotem prędkości |
prędkość rośnie |
ruch przyspieszony |
| wektor przyspieszenia jest skierowany przeciwnie do zwrotu prędkości |
prędkość maleje |
ruch opóźniony |
| wektor przyspieszenia jest skierowany pod kątem do wektora prędkości |
prędkość będzie skręcać (zmienia się kierunek ruchu) |
ruch krzywoliniowy |
Możliwe są oczywiście przypadki mieszane - np. ruch krzywoliniowy przyspieszony, lub krzywoliniowy opóźniony; poza tym ruch może się zmieniać z przyspieszonego na opóźniony itp. |
Przypadek 1:

Przypadek 2:
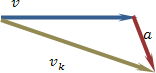
Postać wektorowa definicji przyspieszenia
Do opisu ruchu krzywoliniowego niezbędne jest rozpatrywanie przyspieszenia jako wektora.
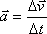
Powyższa postać definicji przyspieszenia informuje nas o tym, że kierunek i zwrot przyspieszenia są zgodne z kierunkiem i zwrotem wektora zmiany prędkości.
Definicja przyspieszenia chwilowego
Wzory
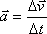
i
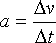
opisują tzw. przyspieszenie średnie, czyli przyspieszenie liczone dla dowolnych, nawet bardzo dużych przedziałów czasu. Jednak podając przyspieszenie najczęściej myślimy o jednej chwili ruchu. Dlatego "prawdziwe" przyspieszenie to tzw. przyspieszenie chwilowe, czyli przyspieszenie liczone dla bardzo małych (właściwie nieskończenie małych) odcinków drogi (lub nieskończenie małych przedziałów czasu). Matematycznie zapisuje się to albo z użyciem pojęcia granicy (limes - łac. granica), albo za pomocą, równoważnej, notacji różniczkowej.
| Przyspieszenie chwilowe |
postać różniczkowa |
postać z użyciem granicy |
| postać skalarna |
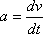 |
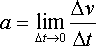 |
| postać wektorowa |
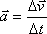 |
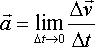 |
Jednostka przyspieszenia
| Jednostką przyspieszenia jest "metr na sekundę kwadrat" |
|
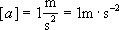 |
Jak przyrasta droga w ruchu jednostajnie zmiennym?
W ruchu jednostajnie zmiennym przyrost drogi zależy od aktualnej wartości prędkości i przyspieszenia.
Opisują to dwa wzory, które można używać zamiennie (wybieramy ten, który jest wygodniejszy w danej sytuacji):
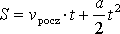
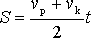
Ja szczególnie polecam ten ostatni wzór, chociaż jest on rzadziej używany. Jednak jest prostszy do zapamiętania i łatwiejszy do przekształceń. Oba wzory są równoważne - wzór pierwszy powstaje z drugiego po podstawieniu wartości:
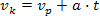
Jest jeszcze jeden pożyteczny wzór na drogę powstający po podstawieniu czasu z wzoru na v końcowe do dowolnego z wzorów na drogę:
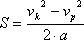
Ważne pojęcia związane z przyspieszeniem
- Ruch jednostajnie zmienny - ruch ze stałym przyspieszeniem.
- Ruch jednostajnie zmienny prostoliniowy - ruch ze stałym przyspieszeniem po linii prostej.
- Ruch jednostajnie przyspieszony - ruch ze stałym przyspieszeniem z rosnącą wartością prędkości.
- Ruch jednostajnie opóźniony - ruch ze stałym przyspieszeniem (opóźnieniem) z malejącą wartością prędkości.
- Ruch niejednostajnie zmienny - ruch ze zmiennym przyspieszeniem.
|