Siła, czyli wielkość zmieniająca stan ruchu ciała

Wielkością która zmienia ruch (pęd) ciała jest siła . Do tego, aby w danej sytuacji pojawiła się siła różna od zera potrzebne są:

• przynajmniej dwa ciała
• oddziaływanie między tymi ciałami

Pojedyncze ciało, choćby nie wiem jak wielkie i jak szybkie nie "stanowi" jeszcze siły - może ono mieć duży pęd, dużą prędkość, wreszcie w stosownej sytuacji może ono zadziałać dużą siłą na inne ciało , ale póki nie ma na co działać - dotąd siły nie ma (!).

Definicja siły

Siłę definiować wzorem można na dwa równoważne (prawie - ale to już wyższa szkoła fizyki) sposoby:

skalarnie		wektorowo
z przyspieszenia (z drugiej zasady dynamiki)		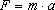	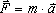wzór najczęściej stosowany w szkole
z pędu		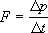	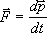wzór często stosowany przez naukowców, a przydatny też w szkole

Gdy istnieje tylko jedno oddziaływanie można powiedzieć, że: Siła działająca na ciało o masie m , związana z danym oddziaływaniem równa jest iloczynowi masy ciała i przyspieszenia nadawanemu ciału przez to oddziaływanie

Lub "pędowo": Siła jest równa szybkości zmiany pędu wywołanej przez dane oddziaływanie

Zaawansowana forma definicji siły

W zaawansowanej formie definiuje się siłę różniczkowo:

z drugiej zasady dynamiki
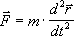z pędu

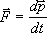Dlaczego siła jest tak ważną wielkością?

Siła jest wielkością niezwykle użyteczną dlatego, że dla bardzo wielu sytuacji możemy z góry określić jaka będzie wartość działających sił. A znając siły można już bardzo wiele powiedzieć na temat zachowania się ciał. Oto przykłady znanych sił:

siła ciężkości (siła grawitacji przy powierzchni Ziemi)	F .g = m .g	m - masa g - przyspieszenie grawitacyjne (na Ziemi - przyspieszenie ziemskie)	wzór słuszny dla ciał znajdujących się w pobliżu powierzchni Ziemi, lub innej planety
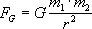
siła grawitacji (ogólnie)		m 1 , m 2 - masy ciał r - odległość między środkami ciał G - stała grawitacji	wzór ogólny, słuszny dla wszystkich odległości i wszystkich kulistych ciał niebieskich
siła sprężysta	F s = - k .x	k - współczynnik sprężystości x - odkształcenie	siła działa zawsze przeciwnie do odkształcenia
siła tarcia posuwistego	T = N .f	N - nacisk na powierzchnię, f - współczynnik tarcia	f może być współczynnikiem tarcia statycznego lub dynamicznego
siła wyporu		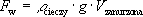g - przyspieszenie ziemskie V - objętość r - gęstość	Liczymy objętość zanurzonej w płynie części ciała
siła parcia płynu	F p = p × S	p - ciśnienie S - pole powierzchni	siła działa prostopadle do powierzchni

Jeżeli na ciało działa więcej niż jedna siła, to ich całkowite działanie uzyskujemy poprzez zsumowanie wektorów sił składowych. Uzyskaną w ten sposób zsumowaną siłę nazywamy siłą wypadkową. Siła ta zastępuje działanie wszystkich sił na raz.

Siła wypadkowa

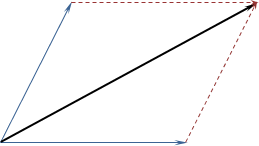
Siła wypadkowa jest sumą wektorową wszystkich sił składowych działających na ciało.

Dwie siły (strzałki niebieskie) po zsumowaniu dają w wyniku inny wektor - wypadkowy (strzałka czarna). Wektory (strzałka czerwona) są wektorami pomocniczymi w graficznym przedstawieniu)

Siła wypadkowa pozwala na wyznaczenie przyspieszenia jakie będzie miało ciało:

Druga zasada dynamiki Newtona

Przyspieszenie jest wprost proporcjonalne do działającej siły wypadkowej działającej na ciało, a odwrotnie proporcjonalne do masy ciała.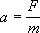

Po co druga zasada dynamiki?

Druga zasada jest sposobem na przewidywanie przyszłości :

• mając informację o siłach działających na ciało możemy wyliczyć przyspieszenie tego ciała znając przyspieszenie możemy wyliczyć prędkość chwilową tego ciała mając prędkość możemy wyliczyć przyszłe położenie ciała
• a mając nowe położenie ciała możemy ustalić nowe siły nań działające (kółko się zamyka)

W efekcie postępując tak odpowiednio długo można wyliczyć dowolne położenie ciała w dowolnej chwili. Wystarczy "tylko" znać położenia wszystkich ciał we wszechświecie i znać wzory na wszystkie możliwe siły. Potem już tylko mieć odpowiednio wydajny komputer...

Przykład zastosowania II zasady Newtona

Jeżeli na rozpędzoną bryłę lodu o masie 5kg działa hamująca o wartości 2N, to opóźnienie tej bryły będzie miało wartość: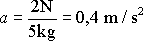

Uwaga!!! - częsty błąd związany z pojęciem siły

Bardzo częstym błędem jest wiązanie sił działających na ciało nie z przyspieszeniem, tylko z prędkością. Większość osób, kierując się mylną intuicją myśli, że aby ciało się poruszało, potrzebne jest stałe działanie siły. Pamiętajmy (!)

siła powoduje PRZYSPIESZENIE, a nie prędkość!!!

na prędkość siła wpływa tylko pośrednio - zmiany prędkości ujawniają się po pewnym czasie działania siły (istnienia niezerowego przyspieszenia).
Lub, inaczej mówiąc: Siła się NIE magazynuje! Ciało zachowuje swój stan ruchu (swoją prędkość) dopóki siła go z tego nie wytrąci! Potocznie rozumiana "siła rozpędu" sama z siebie NIGDY (!!!) się nie wyczerpuje! (lepiej jest nie używać pojęcia "siła rozpędu", bo jest ono błędne z fizycznego punktu widzenia) Dlatego też:

• meteoryt w przestrzeni kosmicznej pędzi miliardy kilometrów, nie zmieniając prędkości (a nie ma żadnego napędu!) kula armatnia leci sobie długo w powietrzu mimo, że nic jej nie napędza (artylerzyści w czasie jej lotu często ładują i wystrzeliwują już kolejną kulę...) do tego żeby zatrzymać rozpędzone ciało trzeba użyć siły przeciwnie skierowanej, a nie tylko czekać aż samo się zatrzyma kula ziemska od wielu miliardów lat pędzi przez Kosmos z ogromną prędkością ok. 30km/s (prawie 100 razy prędkość dźwięku) mimo braku jakiegokolwiek napędu w przypadku braku siły tarcia (np. na lodzie) trudno jest wyhamować rozpędzone ciało
• zatrzymywanie się "zwykłych" ciał po pewnym czasie wynika nie tyle z braku działania siły napędzającej, lecz z faktu istnienia hamującej siły tarcia!