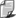Tarcie Tarcie jest siłą przeciwstawiającą się ruchowi obiektów. Tarcie jest zawsze skierowane przeciwnie do prędkości. Nie istnieje ogólna teoria opisująca zjawiska oporów ruchu, ponieważ w grę wchodzą tu mechanizmy różnego rodzaju.

Niektóre przypadki sił oporu ruchu zostały dokładniej zbadane przez fizyków. Należą do nich:

• Tarcie posuwiste
• Tarcie toczne
• Tarcie (opór) aerodynamiczne i hydrodynamiczne

Tarcie posuwiste

Jeżeli będziemy przesuwali względem siebie dwie stykające się powierzchnie, to zaobserwujemy zjawisko tarcia posuwistego.

Przyczyną tego rodzaju tarcia są mikroskopijne zadziory zaczepiające o siebie na trących powierzchniach. Dlatego nawet pozornie gładkie powierzchnie nie ślizgają się swobodnie. Faktem jest natomiast, że dokładne oszlifowanie powierzchni może w wielu przypadkach zmniejszyć tarcie.

Okazuje się, że w typowych sytuacjach tarcia posuwistego stosunek siły tarcia do nacisku trących powierzchni jest stały. Jego wartość nazywana jest współczynnikiem tarcia .

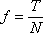
Znaczenie symboli:

f - współczynnik tarcia (wielkość niemianowana)
T - siła tarcia posuwistego (najczęściej w niutonach N)
N - siła dociskająca trące powierzchnie (najczęściej w niutonach N)

Tarcie posuwiste ma swoje dwie odmiany:

• tarcie statyczne
• tarcie dynamiczne

Z przypadkiem tarcia statycznego mamy do czynienia wtedy, gdy zaczynamy przesuwać (ruszamy z miejsca) stykające się powierzchnie różnych ciał. W odróżnieniu do niego tarcie dynamiczne zachodzi już podczas ruchu. Ponieważ najczęściej trudniej jest ruszyć ciało z miejsca, niż później podtrzymywać jego prędkość, to w większości przypadków tarcie statyczne jest większe od dynamicznego.

Różnica między wartością współczynnika tarcia statycznego, a dynamicznego może być różna - jest bardzo duża w przypadku przymarzniętych płóz sań, a mała dla gładkich, twardych powierzchni. Wzór na wartość współczynnika tarcia jest taki sam dla obu jego rodzajów.

Przykład obliczania współczynnika tarcia posuwistego:

Aby worek o masie 50 kg przesuwać po podłodze ciężarówki ze stałą prędkością należy ciągnąć go siłą 100 N. Ile wynosi współczynnik tarcia w tym przypadku?

Rozwiązanie:

Oczywiście mamy do czynienia z tarciem dynamicznym, bo powiedziane jest, o "ciągnięciu" worka, a nie jego ruszaniu. Aby obliczyć współczynnik tarcia trzeba podać obie wielkości występujące po prawej stronie we wzorze:

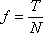
Najpierw licznik, czyli T - tarcie. Z treści zadania wynika bezpośrednio, że

T = 100 N

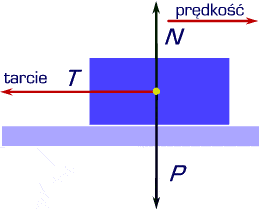
Teraz mianownik - nacisk. Nacisk na klocek pochodzi od podłoża i jest skierowany do góry (podłoga podtrzymuje go). Nacisk jest przeciwny wobec siły ciężkości działającej na klocek, ponieważ musi zrównoważyć tę siłę. Dlatego wartości siły nacisku i siły ciężkości są takie same. Ich zwroty są jednak przeciwne. Jeśli przez N oznaczymy wartość siły nacisku, a przez P wartość siły tarcia, to możemy zapisać:

N = P = m . g

Mamy więc:

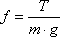
Podstawmy dane:

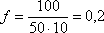
W naszym przypadku współczynnik tarcia dynamicznego wynosi 0,2 (jest to liczba niemianowana, czyli jej jednostka jest równa 1).

Tarcie toczne

W przypadku ciał toczących się wzór na współczynnik tarcia jest inny. Wynika to z faktu, że łatwiej jest toczyć koło (walec) o większym promieniu niż o mniejszym. Dlatego w miarę stałą wartość dla danych powierzchni ma współczynnik obliczany następująco:

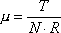
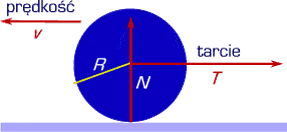
Tutaj podobnie jak poprzednio: m - współczynnik tarcia tocznego (w 1/m = m -1 ) T - siła tarcia tocznego (najczęściej w niutonach N) N - siła dociskająca powierzchnie (najczęściej w niutonach N) oraz R - promień toczącego się koła lub walca (w metrach m)

Tarcie aero- hydrodynamiczne

Ruch obiektów w płynach (pod tym wspólnym mianem będziemy rozumieli zarówno ciecze, jak i gazy) podlega dość złożonym regułom. W szczególności bardzo skomplikowane jest zjawisko burzliwych (wirowych) przepływów płynu.

Stosunkowo najprostsze dla badań są przepływy laminarne (spokojne, bez wirów).

Przestawię dwa proste przypadki praw związanych z oporem płynów: dla małych prędkości dla średnich prędkości

Ruch kulki w płynie z małą prędkością.

Obowiązuje tu tzw. prawo Stokesa:

F T = 6 R h .v

Znaczenie symboli:

• F T - siła oporu płynu (najczęściej w niutonach N)
• R - promień kulki (najczęściej w metrach m)
• h - lepkość płynu (wielkość do znalezienia w tablicach - zazwyczaj w kg/ms)
• v - prędkość kulki (najczęściej w m/s)

Opór płynu dla średnich prędkości ruchu obiektu

Ten przypadek związany jest z ruchem takich obiektów jak samochody, lecące piłki, gołębie itp.

Teraz wzór na siłę oporu aerodynamicznego przyjmie inną postać (wzór Newtona):

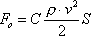
Znaczenie symboli:

• v - prędkość poruszającego się obiektu (najczęściej w m/s)
• r - gęstość płynu (najczęściej w kg/m 3 )
• S - pole przekroju poprzecznego obiektu (w metrach kwadratowych m² )
• C - współczynnik zależny od kształtu ciała (niemianowany)

Producenci samochodów i innych pojazdów starają się, aby współczynnik C miał jak najmniejszą wartość, dzięki czemu zużywają one mniej paliwa.

Tarcie a energia

Z każdym procesem fizycznym można związać jakieś przemiany energii. Powstaje więc pytanie:
Co się dzieje z energią kinetyczną obiektów podlegających tarciu?

- odpowiedź jest dość prosta - w większości przypadków energia ta zamieniana jest na energię cieplną. Dlatego samoloty poruszające się z dużymi prędkościami bardzo się rozgrzewają, opony (felgi) samochodów, które wróciły z trasy są ciepłe, a tarcie kawałków drewna o siebie jest starą metodą rozniecania ognia. Jeżeli w jakimś ruchu pojawia się tarcie, to oznacza, że w ruchu tym energia mechaniczna nie jest zachowana , ponieważ jej część zamienia się na energię wewnętrzną - czyli po prostu ciepło. Mówimy w tym przypadku też o rozpraszaniu energii . Co prawda energia całkowita (czyli uwzględniająca też energię wewnętrzną) dalej jest zachowana, jednak suma energii kinetycznej plus energia potencjalna zmniejsza się.

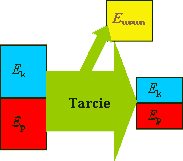
Za przyczyną tarcia jest rozpraszana

Podsumowanie mechanizmów tarcia

Niestety, że nie ma jednolitego wzoru na tarcie aerodynamiczne.
Dla małych prędkości obowiązuje liniowa zależność od prędkości i rozmiarów; dla większych siła rośnie z kwadratem prędkości i rozmiarem. Dla bardzo dużych prędkości siła oporu rośnie z sześcianem prędkości.

Tabela - zależność siły oporu ośrodka od prędkości

Wartość prędkości v	Siła oporu ośrodka
mała	proporcjonalna do v
średnia	proporcjonalna do v 2
duża	proporcjonalna do v 3

Tarcie (opór) nie jest jedyną siłą związaną z ruchem w płynach - wyróżnia się też np. siłę nośną, czy inne siły nie związane z hamowaniem.

Skomplikowany charakter zjawiska tarcia wynika z faktu, że istnieje bardzo wiele czynników nań wpływających:

• tarcie aerodynamiczne zależy od temperatury, lepkości, i gęstości płynu, a także kształtu obiektów,
• tarcie posuwiste może zależeć od pokrycie obiektów smarami, gładkości i ścieralności powierzchni, a także ich wilgotności i temperatury.

W szczególnych przypadkach znaczące mogą być a nawet szczególne "umiejętności" poruszających się obiektów - np. delfiny potrafią mięśniami skóry neutralizować wiry wodne wpływające negatywnie na zdolność ruchu.