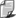 Wektory,
skalary - rodzaje wielkości fizycznych Wektory,
skalary - rodzaje wielkości fizycznych
Wektory,
Skalary - wprowadzenie
W
fizyce mamy najczęściej do czynienia z dwoma rodzajami
wielkości fizycznych:
- wielkościami
skalarnymi (zwykłymi liczbami)
- wielkościami
wektorowymi (opisywanymi albo przez kilka lub więcej
liczb, albo rysowanymi jako strzałki)
Jak
poznać, czy symbol literowy wielkości oznacza wielkość
wektorową, czy skalarną?
Wektory
zapisuje się w podręcznikach najczęściej na dwa sposoby:
- jako
literę oznaczającą wielkość fizyczną ze strzałką
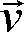
- drukiem
pogrubionym (często też pochyłym ) - np.
F
|
|
|
Skalary
w tekście, to po prostu zwykłe litery, drukowane zazwyczaj
czcionką pochyłą - np. m , t, q .
Wektory
- ujęcie graficzne i analityczne
Wektory
przedstawia się zazwyczaj na dwa sposoby:
- ujęcie
graficzne: czyli strzałka na płaszczyźnie
lub w przestrzeni
- ujęcie
analityczne: układ dwóch liczb - współrzędnych
(na płaszczyźnie), lub trzech liczb (w przestrzeni)
|
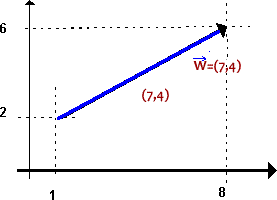 związek
między dwoma ujęciami wektora - strzałką wektora
(ujęcie graficzne) i liczbami opisującymi położenie
początku i końca strzałki związek
między dwoma ujęciami wektora - strzałką wektora
(ujęcie graficzne) i liczbami opisującymi położenie
początku i końca strzałki |
| Współrzędne
wektora otrzymujemy odejmując od współrzędnych
końca wektora, współrzędne początku tego wektora. |
- współrzędna
x - owa wektora w naszym wypadku ma wartość
7 (znajdujemy różnicę współrzędnych końca
i początku wektora 8-1=7)
- współrzędna
y - owa w naszym wypadku ma wartość 4 (bo
6 - 2 = 4)
|
Oba
te ujęcia (graficzne i analityczne) są w zasadzie
równoważne, tzn. dają zgodne ze sobą wyniki. Zaletą
ujęcia graficznego jest lepsze działanie na wyobraźnię,
zaletą ujęcia analitycznego jest łatwość obliczeń
matematycznych oraz możliwość tworzenia wektorów o
więcej niż trzech wymiarach (znacznie trudniej byłoby
wyobrazić sobie np. sześciowymiarowe wektory jako
strzałki).
Różnice
między skalarami, a wektorami
Różnica
między skalarami, a wektorami jest dość subtelna.
Łatwo określić, że coś jest wektorem wtedy, gdy ma
więcej niż jeden wymiar. Jednak wielkość jednowymiarowa
w zasadzie może być uznana zarówno za skalar jak i
za wektor.
|
posiadają:
|
opisują
|
dostępne
działania |
| wektory |
i
najczęściej punkt przyłożenia |
wielkości
działające w jakimś kierunku - np.: siła, pęd
prędkość, przyspieszenie, wektor pola elektrycznego,
indukcja magnetyczna |
- dodawanie
wektorów
- odejmowanie
wektorów
- mnożenie
i dzielenie wektora przez liczbę
- mnożenie
skalarne wektorów
- mnożenie
wektorowe wektorów
- znajdowanie
wartości wektora
|
| skalary |
tylko wartość
i
niekiedy punkt przyłożenia |
wielkości
bezkierunkowe - np. temperatura, masa, ładunek,
gęstość, ciśnienie |
- dodawanie
- odejmowanie
- mnożenie
- dzielenie
- potęgowanie
- funkcje
trygonometryczne, logarytmiczne itp.
|
Korzyści
i ograniczenia opisu wektorowego i skalarnego
|
dodawanie
|
mnożenie
|
inne
działania |
w
e
k
t
o
r
y |
dodawanie
wektorów jest skomplikowane - nie można po prostu
dodać ich wartości; trzeba stosować metody graficzne,
lub geometrię analityczną |
mamy
aż trzy podstawowe rodzaje mnożenia wektorów:
- przez
liczbę
- skalarne
- wektorowe
|
Wektor
można dzielić, ale
nie można dzielić przez wektor! ,
nie ma potęgowania wektorów,
funkcje (trygonometryczne, logarytmiczne)nie działają
na samych wektorach (wektory mogą występować jako
argumenty tych funkcji ale nigdy samodzielnie
- najczęściej są w parze w iloczynie skalarnym
z drugim wektorem) |
s
k
a
l
a
r
y |
łatwo
jest je dodawać - bo zwyczajnie dodaje się liczby |
zwykłe
mnożenie, ew. mnożenie przez wektor (patrz wyżej) |
istnieją
operatory, które pola skalarne przekształcają
w pola wektorowe (ale to już "wyższa szkoła jazdy") |
Jeżeli
wektor pozbawimy kierunku i zwrotu, wtedy będzie on
skalarem. Np. prędkość jest wektorem, ale wartość
prędkości jest skalarem o wartości nieujemnej.
Wartość
wektora
Operację
pobierania z wektora jego wartości (tzw. moduł wektora)
zapisuje się symbolicznie za pomocą kresek otaczających
symbol wektora.
Wartość
jest szczególnym typem skalara, gdyż:
wartość
wektora (niezerowego) jest zawsze dodatnia. 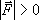
W
przypadku gdy znamy współrzędne wektora, wtedy jego
wartość obliczamy z twierdzenia Pitagorasa:
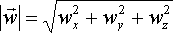 |
- podnosimy
wszystkie współrzędne do kwadratu
- sumujemy
uzyskane kwadraty współrzędnych
- wyciągamy
pierwiastek kwadratowy z sumy.
|
Działania
na wektorach
| rodzaj
działania |
zapis
i typ wielkości wynikowej |
opis
wielkości wynikowej |
| mnożenie
wektora przez liczbę
Tak samo dzielenie przez liczbę. |
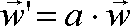
otrzymujemy
nowy wektor
Aby
wektor podzielić przez liczbę, mnożymy go przez
odwrotność tej liczby |
powstaje
wektor a razy dłuższy od wektora wyjściowego
zwrot wektora wynikowego jest:
- taki sam jak wyjściowy, gdy a jest
dodatnie
- przeciwny do wyjściowego, gdy a jest
ujemne
Wynik może być równy zero (będzie tzw. wektorem
zerowym) gdy:
- wektor wyjściowy jest równy zero, lub
- liczba a jest równa zero |
| mnożenie
skalarne wektorów |
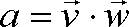
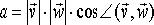
otrzymujemy
skalar |
Powstaje
liczba (skalar) o wartości równej iloczynowi wartości
obu wektorów razy kosinus kąta między nimi zawartego.
Lub
inaczej:
Iloczyn skalarny jest równy iloczynowi długości
jednego wektora mnożonego przez długość rzutu
drugiego wektora na kierunek wyznaczony przez
pierwszy wektor (skomplikowane jest to zdanie,
ale prościej chyba się nie da...).
Iloczyn
skalarny stanie się równy Zero, gdy którykolwiek
z wektorów wyjściowych jest zerowy, lub wektory
są prostopadłe. |
| mnożenie
wektorowe wektorów (stosuje się do wektorów
w trzech wymiarach)
Uwaga: w rzeczywistości efektem mnożenia wektorowego
wektorów jest tensor... Ale w uproszczeniu możemy
go traktować jako wektor. |
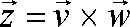
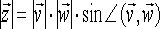
otrzymujemy
nowy wektor prostopadły do
obu wektorów wyjściowych |
-
wartość wektora wynikowego jest równa iloczynowi
wartości obu wektorów wyjściowych razy sinus kąta
między nimi zawartego (ma to sens tylko w trzech
wymiarach);
- kierunek wektora wynikowego jest prostopadły
do płaszczyzny wyznaczonej przez wektory wyjściowe;
- zwrot ustalamy w oparciu o regułę śruby prawoskrętnej
Interpretacja
iloczynu wektorowego 2:
Wartość iloczynu wektorowego jest równa iloczynowi
długości pierwszego wektora przez długość rzutu
drugiego wektora na kierunek prostopadły do
pierwszego wektora.
Wektor
zerowy otrzymamy, gdy jeden z wektorów wyjściowych
jest zerowy, lub gdy wyjściowe wektory są równoległe |
| znajdowanie
wartości wektora |
na
płaszczyźnie: 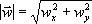
w
przestrzeni: 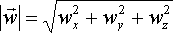
otrzymujemy
skalar |
Długość
wektora na płaszczyźnie obliczamy stosując twierdzenie
Pitagorasa. Żeby obliczyć wartość wektora trójwymiarowego
trzeba zastosować to twierdzenie dwa razy.
Długość wektora jest równa zero tylko wtedy,
gdy wszystkie współrzędne
wektora są równe zero. |
Na
koniec jeszcze wzory i przykłady działań na wektorach
w postaci analitycznej.
| Przedstawię
tylko nasze dane: |
| liczba
a |
w
przykładzie a = 3 |
i
wektory:
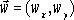
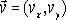 |
w
przykładzie:
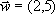
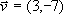 |
| rodzaj
działania |
zapis
|
Przykład
i komentarz |
| mnożenie
przez liczbę |
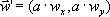
|
3
× (2,5)=(6,15)
mnożymy przez liczbę, każdą ze współrzędnych wektora. |
| Mnożenie
skalarne wektorów |
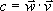
c
= w x × v x + w y× v y |
(2,5)
× (3,-7)=6+(-35)=-29
mnożymy przez siebie współrzędne obu wektorów,
a otrzymane iloczyny dodajemy |
| mnożenie
wektorowe wektorów |
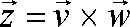
To
jest tylko wzór na wartość wektora!
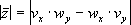
|
Wartość
iloczynu wektorowego wektorów (2,5) i (3,-7)
|(2,5)
x (3,7)| = |-14 -15|=|-29|=29
Aby
otrzymać wartość iloczynu
wektorowego, mnożymy współrzędne "na krzyż",
otrzymane iloczyny odejmujemy i wyciągamy wartość
bezwzględną z wyniku. |
| znajdowanie
wartości wektora |
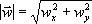
|
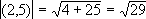
Podnosimy współrzędne do kwadratu, wyniki dodajemy,
a otrzymaną sumę pierwiastkujemy. |
Istnieje
oczywiście wzór na wszystkie składowe iloczynu wektorowego,
ale licealnym programie fizyki nie jest on ani uwzględniony,
ani wykorzystany. Pełną tabelę, łącznie ze wspomnianym
wzorem, zamieszczę w ostatecznej CD - romowej wersji
Słowniczka.
Rozkład
wektora na kierunki składowe - rzutowanie
Każdy
wektor można zrzutować na dowolny kierunek. Operacja
taka pozwala na ustalenie jaka część tego wektora
"przypada" na ten kierunek. Np. aby dowiedzieć
się jak bardzo siła 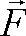 "ciągnie" w kierunku a , rzutujemy wektor "ciągnie" w kierunku a , rzutujemy wektor
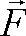 na
prostą a . na
prostą a . |
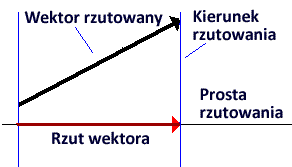 |
| Najczęstszym
rodzajem rzutowania jest rzut prostokątny (jest
on przedstawiony na rysunku). Dla takiego rzutu
kierunek rzutowania jest prostopadły do prostej,
na którą rzutujemy. |
Szczególny
przypadek - wektor jednowymiarowy (sprawa ważna,
niełatwa, a w książkach nie omawiana)
Szczególnym
przypadkiem wielkości, która jest czymś pośrednim
między wektorem, a skalarem, jest wektor
jednowymiarowy . Jest to wielkość w fizyce
bardzo ważna, bo będąc formalnie wektorem, nie
posiada wad formalizmu wektorowego (kłopotliwości
rachunkowych, wielu wymiarów do przekształcania)
i dlatego jest bardzo często wykorzystywana. Za
pomocą tej wielkości opisuje się wszystkie procesy
zachodzące w jednym wymiarze. Np.
- prędkość
w ruchu prostoliniowym (lub po ściśle określonym
torze)
- przyspieszenie
w ruchu prostoliniowym (lub po ściśle określonym
torze)
- siła
w ruchu prostoliniowym (lub po ściśle określonym
torze)
|
:
Najważniejszą różnicą między wektorem jednowymiarowym
z wartością wektora jest to, że wartość może być tylko
dodatnia, a wektor jednowymiarowy może być zarówno
dodatni, jak i ujemny.
To jaki jest znak tej wielkości zależy od Umowy Znaku
Osi . Umowa ta polega na tym, że najpierw wyróżniamy
jeden zwrot naszego ruchu jako dodatni. Od tej pory
wszystkie wielkości mające zgodny zwrot będziemy traktować
jako dodatnie. Zwrot przeciwny odpowiada oczywiście
wartościom ujemnym.
Np. w sytuacji na rysunku:
|
- V
1 jest dodatnie np. V 1 = 4
- V
2 jest ujemne V 2 = -7
- V
3 jest ujemne V 3 = - 4
- V
4 jest dodatnie V 4 = 8
|
Wektory
jednowymiarowe można traktować jak zwykłe liczby -
można je mnożyć jak liczby, dzielić; a nawet dzielić
przez taki "wektor" (napisałem go
w cudzysłowie, bo jeszcze komuś przyjdzie do głowy
dzielić przez inne "prawdziwe" wektory, a to jest
karalne! art. 123 par. 456, coś tam 789). Jednym słowem
można robić z nim wszystko co ze zwykłymi liczbami
- nawet potęgować, pierwiastkować, znajdować sinusy
itp.
Dzięki takiemu przedstawieniu wielkości wszystkie
wzory opisujące np. ruch przyspieszony i opóźniony
są identyczne, podobnie jednolicie można opisywać
siły elektrostatyczne i wiele innych.
W
zasadzie tylko dzięki takim jednowymiarowym wektorom
można zinterpretować minus, który nagle pojawia się
w wyniku obliczanej przez nas wielkości. Wartość wektora
jednowymiarowego otrzymujemy biorąc po prostu wartość
bezwzględną z liczby opisującej ten wektor.
W
przypadku wektorów jednowymiarowych nie ma potrzeby
rozważać kierunku bo jest on ustalony. Wystarczy mówić
o wartości i zwrocie.
Podsumujmy
zalety wektorów jednowymiarowych:
- dodawanie
i odejmowanie odbywa się jak zwykłe dodawanie liczb
- mnożenie
skalarne to zwykłe mnożenie liczb
- wielkość
ta może być umieszczana w mianowniku wzorów (można
przez nią dzielić)
Większość
problemów fizycznych o charakterze rachunkowym rozwiązuje
się poprzez sprowadzenie wektorów do przypadków jednowymiarowych
i tam wykonywanie już rachunków w tej prostszej postaci.
Dla
ekspertów i ciekawskich, czyli zaawansowana wiedza
o rachunku wektorowym
| Fizycy
używają jeszcze jednego, bardziej zaawansowanego
typu wielkości fizycznych: tensora. Tensory
są rozszerzeniem pojęcia wektora. Używa się ich
do opisu odkształceń w ośrodkach, zachowania się
bryły sztywnej, podczas obrotów w trzech wymiarach,
w teorii pola (np. w ogólnej teorii względności
Ensteina) i w wielu innych sytuacjach. |
| W
pewnym uproszczeniu tensor możemy sobie wyobrażać
jako operator działający na wektor i produkujący
z niego nowy wektor o innym zwrocie, kierunku
i wartości. Jest to więc więcej niż mnożenie wektora
przez liczbę (taka operacja nie zmienia kierunku
wektora), więcej niż mnożenie wektorowe wektorów
(bo wtedy otrzymujemy zawsze wektor prostopadły
do płaszyczyzny wyznaczonej przez wektory wyjściowe)
i coś zupełnie innego niż mnożenie skalarne wektorów,
czy znajdowanie wartości wektora (bo z tych ostatnich
operacji w wyniku otrzymujemy skalar).
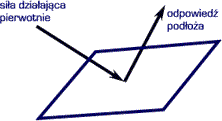
A
oto przykład sytuacji, do opisu której niezbędny
jest tensor: wyobraźmy sobie, że chcemy opisywać
siłę jaka działa zwrotnie (reakcja) po zadziałaniu
naszą siłą na jakąś powierzchnię. My możemy
działać siłą w kierunku A, ale ponieważ powierzchnia
może być ustawiona pod kątem, może sprężynować,
może być mniej lub bardziej śliska, więc reakcja
tej powierzchni może być pod kątem do kierunku
siły pierwotnej, może powodować poślizg, czy
skręcenie pod jakimś innym kątem. |
Przykłady:
wektory
|
skalary
|
| siła,
prędkość, przyspieszenie, przesunięcie, pęd, indukcja
magnetyczna, natężenie pola elektrycznego |
masa,
temperatura, gęstość, ciśnienie, energia, czas. |
|