 Przybornik ucznia fizyki
Przybornik ucznia fizyki
Odczytywanie i interpretacja wzorów.
Prawa fizyki są najczęściej zapisywane w postaci wzorów matematycznych. Dlatego niezbędną umiejętnością każdego fizyka, jest odczytywanie i interpretacja zależności tak przedstawionych.
Odczytywanie praw i wzorów
Istnieją proste reguły, które pozwalają wzór matematyczny przetłumaczyć na "język mówiony", czyli inaczej mówiąc, poprawnie przeczytać. Przy odczytywaniu praw fizycznych, stosujemy następujące zasady: jeżeli symbol pewnej wielkości występuje w liczniku wzoru, to mówimy, że wynik jest do niej wprost proporcjonalny, jeżeli występuje w mianowniku, to wynik jest do tej wielkości odwrotnie proporcjonalny.
Przykład 1
Prawo (II zasada dynamiki):
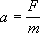
czytamy: a jest wprost proporcjonalne do F i odwrotnie proporcjonalne do m.
Przykład 2:
Prawo "Ohma"
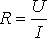
czytamy: R jest wprost proporcjonalne do U
Odczytywanie skrótowe praw fizycznych
Wypowiadając zapisane wzorem prawo fizyczne najczęściej robimy to sposobem skróconym tzn. opuszczamy stałe fizyczne i matematyczne, a więc wielkości, które nie zmieniają się przy zmianie sytuacji np. prawo grawitacji:
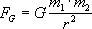
odczytamy:
"F jest wprost proporcjonalne do iloczynu m1 i m2 i odwrotnie proporcjonalne do r kwadrat",
za G będące stałą fizyczną, przy odczytywaniu prawa pomijamy.
Odczytywanie wzorów
Gdy zachodzi potrzeba dokładnego przeczytania wzoru, np. w celu konkretnego podania jakiej wielkości, wtedy oczywiście odczytujemy całą jego treść, łącznie ze wszystkimi stałymi. Wzoru najczęściej nie odczytujemy jako "proporcjonalne do..." lecz "równe...". W przypadku prawa grawitacji, wzór je wyrażający przeczytamy:
"F jest równe iloczynowi G, m1 i m2 , dzielone przez r kwadrat"
Przykłady:
1. Wzór
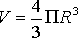
przeczytamy: "V jest równe cztery trzecie pi R do trzeciej"
2. Wzór
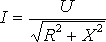
(nie zawiera stałych fizycznych) można przeczytać:
- pierwszy sposób: "I jest wprost proporcjonalne do U i odwrotnie proporcjonalne do pierwiastka z sumy R kwadrat plus X kwadrat", lub
- drugi sposób: "I jest wprost proporcjonalne do U i odwrotnie proporcjonalne do sumy R kwadrat plus X kwadrat do potęgi 1/2" (pierwiastek kwadratowy jest równoważny podniesieniu do potęgi o wykładniku 1/2).
3. Prawo Ohma
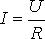
- czytamy: I jest proporcjonalne do U (R w tym wzorze jest stałą).
Jak z tego widać, że prawa i wzory najczęściej można przeczytać poprawnie na kilka sposobów.
Interpretacja wzorów
Ważniejszą i trudniejszą umiejętnością niż odczytywanie wzorów, jest dla fizyka prawidłowe ich interpretowanie. Interpretowanie wzorów jest procesem w dużym stopniu twórczym i wymagającym niekiedy indywidualnego podejścia, czy specjalnego pomysłu. Umiejętność nowego interpretowania znanych wcześniej wzorów doprowadzała często w przeszłości do odkryć fizycznych, lub przynajmniej naprowadzała na trop takich odkryć. Nie ma jednak prostej metody na zdobycie nagrody Nobla dzięki interpretacji wzorów z kinematyki, czy dynamiki, więc postaramy się przynajmniej o przedstawienie kilku zasad, pozwalających na interpretowanie wzorów w prostszych przypadkach. Oto one:
Wielkości wprost proporcjonalne
wzór: y=A x, gdzie A - wielkość stała, nie zależna od x.
Jeżeli jaka wielkość fizyczna "y" jest wprost proporcjonalna do innej wielkości "x" (mówimy też, że są od siebie zależne liniowo), to oznacza to, że n-krotne zwiększenie wielkości "x" spowoduje n-krotne zwiększenie wielkości "y"; oczywiście jeżeli pozostałe, występujące we wzorze wielkości nie ulegną osobnej zmianie.
Wykresem zależności proporcjonalnej jest linia prosta.
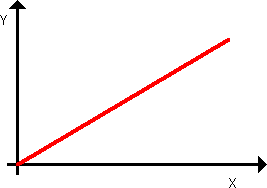
Przykład: zinterpretujmy prawo:
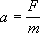
- z postaci wzoru wynika, że
dwukrotne zwiększenie F spowoduje automatycznie dwukrotne zwiększenie a, pięciokrotne zwiększenie F spowoduje pięciokrotne zwiększenie a; analogicznie zwiększenie 7-krotne, 12-krotne, 9,5-krotne itd.
Jeżeli F zmaleje n-krotnie, to a też zmaleje n-krotnie.
Wielkości odwrotnie proporcjonalne
czyli wielkości typu
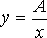 , ,
gdzie A - jest stałe
gdy wielkość "y" jest odwrotnie proporcjonalna do wielkości "x" to oznacza to, że n-krotne zwiększenie "x" spowoduje n-krotne zmniejszenie "y".
Wykresem zależności odwrotnie proporcjonalnej jest hiperbola
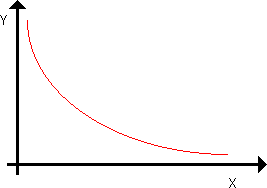
Przykład: znów zinterpretujmy wzór
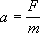
pod względem zależności F od m:
-- dwukrotne zwiększenie m spowoduje dwukrotne zmniejszenie a; analogicznie zwiększenie 3-krotne, 12-krotne, 9,5-krotne itd.
-- gdy m zmaleje n-krotnie, to a wzrośnie n-krotnie (stąd nazwa "odwrotnie" proporcjonalne).
W podsumowaniu punktów a) i b) można powiedzieć, że wzrost wielkości znajdujących się w liczniku wzoru wpływa na wzrost wyniku, za to co jest w mianowniku powoduje zmniejszanie wyniku (oczywiście nie dotyczy to sytuacji, gdy przed wzorem stoi znak "minus", bo wtedy zwiększamy wielkość "w minusy", zatem zależność będzie odwrotna).
Potęgi i pierwiastki
jeżeli jaka wielkość jest podniesiona we wzorze do n-tej potęgi { 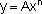 } (n>1), oznacza to, że wzrost tej wielkości wpływa na wzrost wyniku. Wpływ ten jest jednak silniejszy niż w przypadku zależności liniowej. } (n>1), oznacza to, że wzrost tej wielkości wpływa na wzrost wyniku. Wpływ ten jest jednak silniejszy niż w przypadku zależności liniowej.
jeżeli jaka wielkość jest pod pierwiastkiem { 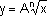 }(kwadratowym, 3-ciego, n-tego stopnia) umieszczonym w liczniku, oznacza to, że wzrost tej wielkości wpływa na wzrost wyniku. Jednak wpływ ten jest słabszy niż w przypadku zależności liniowej (wielkości w pierwszej potędze). Np.: }(kwadratowym, 3-ciego, n-tego stopnia) umieszczonym w liczniku, oznacza to, że wzrost tej wielkości wpływa na wzrost wyniku. Jednak wpływ ten jest słabszy niż w przypadku zależności liniowej (wielkości w pierwszej potędze). Np.:
- we wzorze 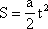 , dwukrotny przyrost t spowoduje czterokrotny przyrost S. , dwukrotny przyrost t spowoduje czterokrotny przyrost S.
- we wzorze 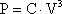 , dwukrotny przyrost V spowoduje ośmiokrotny przyrost P. , dwukrotny przyrost V spowoduje ośmiokrotny przyrost P.
- we wzorze 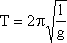 dwukrotny wzrost l spowoduje jedynie ok. 1,4 krotny wzrost T. dwukrotny wzrost l spowoduje jedynie ok. 1,4 krotny wzrost T.
Inne funkcje
Funkcja sin(a)
dla kątów do 90° sinus jest funkcją rosnącą, w związku z czym wzrost kąta powoduje wzrost sinusa. Jednak (z wyjątkiem bardzo niewielkiego przedziału od 0° do 5°, najwyżej do 8°) nie jest to wzrost proporcjonalny - dla większych kątów wartość sinusa rośnie coraz wolniej niż wartość kąta.
Funkcja tg(a)
Do 90° tangens jest funkcją rosnącą. Z tym, że dla małych kątów (od zera do 5°) przyrost jest z grubsza proporcjonalny, ale później tangens rośnie coraz szybciej, osiągając w pobliżu 90° "niebotyczne" wartości (dąży do nieskończoności).
Funkcja cos(a)
Cosinus dla małych katów jest w przybliżeniu równy 1, później za, przy wzroście kąta wartość tej funkcji maleje, aż do zera dla kąta 90°.
Funkcja logarytm log(x) lub ln(x)
Logarytm rośnie wraz ze wzrostem x, ale odbywa się to powoli i to im większy x, to tym wolniej. Np. gdy x zmienia się od 1 do 10 wtedy logarytm rośnie o 1, za gdy x rośnie od 10 do 20, wtedy logarytm rośnie tylko o ok. 0,3. Dla x mniejszego od 1, logarytm ma wartość ujemną.
Przykłady
1. we wzorze P = I2R 2-krotny wzrost I, spowoduje 4-krotny wzrost P,
3-krotny wzrost I spowoduje 9-krotny wzrost P.
2. we wzorze 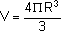
2-krotny wzrost R, spowoduje 8-krotny wzrost V
3-krotny wzrost R, spowoduje 27-krotny wzrost V itd.
3. dla wzoru 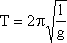 interpretacja zależności T od g jest następująca: interpretacja zależności T od g jest następująca:
gdy g wzrasta 2 razy, to T maleje pierwiastek z 2 razy;
gdy l wzrasta 4 razy, to T maleje 2 razy itd.
Ćwiczenia
1. Dany jest wzór: 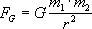 (G jest stałe) (G jest stałe)
Jak zmieni się F (wzrośnie, czy zmaleje i ile razy) jeżeli:
a) m1 wzrośnie 5 razy, a pozostałe wielkości nie zmienią się,
b) m2 zmaleje 4 razy, a pozostałe wielkości nie zmienią się,
c) R zmaleje 4 razy, a pozostałe wielkości nie zmienią się,
d) R wzrośnie 3 razy, a pozostałe wielkości nie zmienią się,
e) R zmaleje 4 razy, a m1 wzrośnie 2 razy,
f) m1 zmaleje 4 razy, a m1 wzrośnie 2 razy,
g) R zmaleje 3 razy, a m1 wzrośnie 2 razy, a m2 5 razy,
h) R zmaleje 4 razy, a m1 zmaleje 3 razy, a m2 wzrośnie 2 razy,
i) R, m1 i m2 wzrosną po 14 razy,<
j) R zmaleje n razy, a m1 wzrośnie k razy,
k) R zmaleje l razy, m1 zmaleje n razy, a m2 wzrośnie k razy?
|