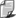 Zagadka ruchu
Zagadka ruchu
Dopóki zajmujemy się ruchem po linii prostej, daleko nam do zrozumienia ruchów, które obserwujemy w przyrodzie. Musimy się zająć ruchami po torach zakrzywionych, toteż nasz następny krok polegać będzie na określeniu praw rządzących takimi właśnie ruchami. Nie jest to łatwe zadanie. Nasze pojęcia prędkości, zmiany prędkości i siły okazały się bardzo pożyteczne w przypadku ruchu prostoliniowego. Nie widać jednak, jak można by je zastosować do ruchu po torze zakrzywionym. Można by nawet przypuścić, że stare pojęcia nie nadają się do opisu ruchu ogólnego i że trzeba stworzyć nowe. Czy powinniśmy próbować postępować starą drogą, czy też wypadnie nam szukać nowej?
Uogólnianie pojęcia jest procesem często w nauce spotykanym. Metoda uogólniania nie jest określona w sposób jednoznaczny, ponieważ uogólniać można zwykle na liczne sposoby. Jeden warunek musi być wszakże ściśle spełniony: pojęcie uogólnione powinno się sprowadzać do pojęcia początkowego, gdy spełnione są te same, co na początku warunki.
Można to najlepiej wytłumaczyć na przykładzie, którym się właśnie zajmujemy. Możemy spróbować uogólnić stare pojęcia prędkości, zmiany prędkości i siły tak, aby obejmowały one również przypadek ruchu po torze zakrzywionym. W języku fachowym, mówiąc o liniach krzywych, włączamy w to również linie proste. Linia prosta jest szczególnym i banalnym przykładem krzywej. Jeśli więc wprowadzić prędkość, zmianę prędkości i siłę dla ruchu po linii krzywej, to są one tym samym automatycznie wprowadzone dla ruchu po linii prostej. Wynik ten nie może jednak być sprzeczny z danymi uzyskanymi uprzednio. Gdy krzywa staje się linią prostą, wszystkie pojęcia uogólnione muszą się sprowadzać do dobrze już znanych pojęć opisujących ruch prostoliniowy. To ograniczenie nie wystarcza jednak, by uogólnienie było wyznaczone w sposób jednoznaczny. Pozostaje jeszcze wiele otwartych możliwości. Historia nauki uczy, że najprostsze uogólnienia czasem okazują się pożyteczne, a czasem nie. Musimy z początku zdać się na domysł. W naszym przypadku łatwo jest odgadnąć właściwą metodę uogólniania. Nowe pojęcia okazują się bardzo udatne, pomagając nam w zrozumieniu zarówno ruchu rzuconego kamienia, jak i ruchu planet.
Cóż więc oznaczają słowa "prędkość", "zmiana prędkości" i "siła" w ogólnym przypadku ruchu po linii krzywej? Zacznijmy od prędkości. Przypuśćmy, że bardzo małe ciało porusza się po krzywej z lewa na prawo. Takie małe ciało bywa często nazywane cząstką . Na naszym rysunku kropka na krzywej wskazuje położenie cząstki w pewnej chwili. Jaka prędkość odpowiada tej chwili i temu położeniu?

Znów trop Galileusza podsuwa sposób wprowadzenia prędkości. Raz jeszcze musimy się odwołać do naszej wyobraźni i przedstawić sobie wyidelizowane doświadczenie. Cząstka porusza się po krzywej z lewa na prawo pod wpływem sił zewnętrznych. Przypuśćmy, że w pewnej chwili, w punkcie oznaczonym kropką wszystkie te siły przestają nagle działać. Zgodnie z prawem bezwładności ruch musi wtedy być jednostajny. Oczywiście w praktyce nigdy nie możemy całkowicie uwolnić ciała od wszystkich wpływów zewnętrznych. Możemy się tylko domyślać "co by było gdyby...?", a trafność przewidywania oceniać na podstawie wniosków, które z niego można wyciągnąć, i ich zgodności z doświadczeniem.
Wektor na następnym rysunku oznacza przewidywany kierunek ruchu jednostajnego, jeśliby wszystkie siły zewnętrzne zniknęły. Jest to kierunek tak zwanej linii stycznej. Patrząc na poruszającą się cząstkę przez mikroskop, widzimy bardzo mały fragment krzywej, który wydaje się krótkim odcinkiem. Styczna jest przedłużeniem tego odcinka. Tak więc narysowany wektor przedstawia prędkość w danej chwili. Wektor prędkości leży na stycznej.

Jego długość przedstawia wielkość prędkości, czyli szybkość - tak jak ją wskazuje na przykład szybkościomierz samochodu.
Naszego wyidealizowanego doświadczenia, polegającego na zniszczeniu ruchu w celu znalezienia wektora prędkości, nie należy brać zbyt poważnie. Pomaga nam ono tylko zrozumieć, co powinniśmy nazwać wektorem prędkości, i pozwala określić ten wektor w danej chwili i w danym punkcie.
Na następnym rysunku pokazano wektory prędkości odpowiadające trzem różnym położeniom cząstki poruszającej się po krzywej. W tym przypadku zmianie w trakcie ruchu ulega nie tylko kierunek, ale również wielkość prędkości, na co wskazuje długość wektorów.
Czy to nowe pojęcie prędkości spełnia wymagania sformułowane dla wszystkich uogólnień? To znaczy - czy w przypadku, gdy krzywa staje się linią prosta, sprowadza się ono do pojęcia już znanego? Oczywiście, tak. Styczną do linii prostej jest sama linia prosta.
Wektor prędkości leży na linii ruchu, tak samo jak to się działo w przypadku poruszającego się wózka czy toczących się kul.
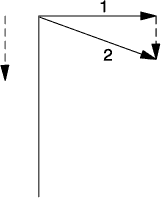
Naszym następnym krokiem będzie wprowadzenie zmiany prędkości cząstki, poruszającej się po krzywej. Również i tego można dokonać na kilka sposobów, z których wybierzemy najprostszy i najwygodniejszy. Na poprzednim rysunku pokazano kilka wektorów prędkości, przedstawiających ruch w różnych punktach toru. Pierwsze dwa można przerysować tak, by miały wspólny początek, co - jak widzieliśmy - jest dla wektorów możliwe.

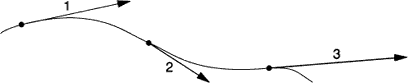
Wektor przerywany nazywamy zmianą prędkości. Jego początek leży w końcu wektora pierwszego, a koniec - w końcu wektora drugiego. Taka definicja zmiany prędkości może się na pierwszy rzut oka wydawać sztuczna i bez sensu. Staje się ona znacznie jaśniejsza w przypadku szczególnym, w którym wektory (1) i (2) mają ten sam kierunek. Oznacza to oczywiście przejście do przypadku ruchu prostoliniowego. Jeżeli oba wektory mają wspólny początek, to teraz wektor kreskowany łączy ich końce. Rysunek jest teraz identyczny z rysunkiem z poprzedniego fragmentu, a poprzednie pojęcie okazuje się szczególnym przypadkiem nowego.
Należy zaznaczyć, że na rysunku musieliśmy dwie linie rozdzielić, gdyż inaczej pokrywałyby się one nawzajem i nie można by ich było odróżnić.
W naszym procesie uogólniania dokonamy teraz ostatniego kroku. Będzie to najważniejsze z wszystkich dotychczasowych przewidywań. Musimy ustalić związek pomiędzy siłą i zmianą prędkości, aby móc znaleźć trop, który pozwoli nam zrozumieć ogólny problem ruchu.
Klucz do objaśnienia ruchu po linii prostej był nieskomplikowany: zmiana prędkości spowodowana jest działaniem siły zewnętrznej, wektor siły ma kierunek taki sam jak zmiana prędkości. A co przyjąć za klucz do objaśnienia ruchu krzywoliniowego? Dokładnie to samo! Jedyna różnica polega na tym, że zmiana prędkości ma teraz szersze niż uprzednio znaczenie. Sprawę wyjaśnia rzut oka na wektory przerywane z ostatnich dwóch rysunków. Jeżeli znana jest prędkość w każdym punkcie krzywej, to można natychmiast znaleźć kierunek siły w dowolnym punkcie. Trzeba narysować wektory prędkości w dwóch chwilach oddzielonych bardzo krótkim odstępem czasu, a więc odpowiadających bardzo bliskim sobie położeniom. Wektor przeprowadzony z końca pierwszego wektora do końca drugiego wskazuje kierunek siły działającej. Istotne jest jednak, aby oba wektory prędkości oddzielone były "bardzo krótkim" odstępem czasu. Ścisła analiza słów takich, jak "bardzo bliski", "bardzo krótki", bynajmniej nie jest prosta. Właśnie ta analiza doprowadziła Newtona i Leibniza do wynalezienia rachunku różniczkowego.
Droga wiodąca do uogólnienia tropu Galileusza jest żmudna i uciążliwa. Nie możemy tu wykazać, jak liczne i owocne są wnioski, które z tego uogólnienia wynikają. Jego zastosowanie prowadzi do prostego i przekonującego wyjaśnienia wielu faktów, które przedtem wydawały się nie związane z sobą i niezrozumiałe.
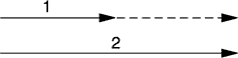
Z ogromnego bogactwa rozmaitych ruchów wybierzemy najprostsze i zastosujemy do nich sformułowane przed chwilą prawo. Tor pocisku wystrzelonego z działa, tor kamienia rzuconego pod kątem do poziomu, tor strumienia wody tryskającego z sikawki - te wszystkie dobrze znane tory są jednakowego typu: mają kształt paraboli. Wyobraźmy sobie na przykład, że do kamienia przymocowany jest szybkościomierz; możemy więc narysować wektor prędkości w dowolnej chwili. Przypuśćmy, że wynik jest taki, jak przedstawiono na rysunku poniżej. Kierunek siły działającej na kamień jest taki sam, jak kierunek zmiany prędkości, a ten umiemy już określać. Wynik - przedstawiony na następnym rysunku - wskazuje, że siła jest pionowa i skierowana w dół.
Mamy tu sytuację zupełnie taką samą, jak w przypadku kamienia puszczonego swobodnie ze szczytu wieży. Tory, a także prędkości, są w obu wypadkach zupełnie różne, jednakże zmiana prędkości ma kierunek ten sam, to znaczy, jest skierowana do środka Ziemi.

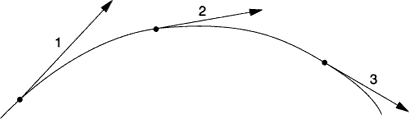
Kamień, uwiązany na sznurku i wirujący w płaszczyźnie poziomej, porusza się po torze kołowym. Jeżeli szybkość jest stała, to wszystkie wektory na wykresie przedstawiającym ruch mają jednakową długość. Jednakże prędkość nie jest stała, bo tor nie jest linią prostą. Jedynym ruchem, przy którym nie działają siły, jest ruch jednostajny prostoliniowy. Tym razem jednak siły działają i prędkość się zmienia - nie co do wielkości, lecz co do kierunku. Zmiana ta, według prawa ruchu, musi być spowodowana przez siłę - w tym wypadku przez siłę działającą między kamieniem a ręką trzymającą sznurek.
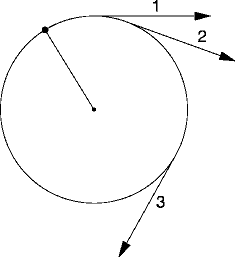
Natychmiast nasuwa się kolejne pytanie: w jakim kierunku działa siła? Odpowiedź daje znów wykres wektorowy. Narysowano tu wektory prędkości odpowiadające dwóm bliskim sobie punktom i znaleziono zmianę prędkości. Ten ostatni wektor jest, jak widać, skierowany wzdłuż sznurka, w stronę środka koła i jest zawsze prostopadły do wektora prędkości, czyli do stycznej. Innymi słowy, ręka działa na kamień siłą za pośrednictwem sznurka.
Podobnym, ale o wiele ważniejszym przykładem jest obrót Księżyca dokoła Ziemi. Obrót ten można w przybliżeniu przedstawić jako ruch jednostajny po kole. Siła jest tu skierowana ku Ziemi z tego samego powodu, dla którego w naszym poprzednim przykładzie była skierowana ku ręce. Choć Ziemi z Księżycem nie łączy sznurek, to jednak możemy sobie wyobrazić linię łączącą środki obu ciał, siła leży na tej właśnie linii i jest skierowana w stronę środka Ziemi, zupełnie tak samo jak siła działająca na kamień rzucony w powietrze lub puszczony z wieży.
Wszystko, cośmy dotąd powiedzieli na temat ruchu, można streścić w jednym zdaniu. Siła i zmiana prędkości są wektorami o jednakowym kierunku . Jest to wstępny trop do rozwiązania problemu ruchu, z pewnością jednak nie wystarczający do pełnego wyjaśnienia wszystkich spotykanych ruchów. Przejście od sposobu myślenia Arystotelesa do sposobu myślenia Galileusza stało się kamieniem węgielnym nauki. Po dokonaniu tego wyłomu droga dalszego rozwoju stanęła otworem. Interesujemy się tu wczesnymi stadiami rozwoju, śledzimy pierwsze tropy, wskazujemy, jak w pełnej bólu walce ze starymi ideami rodzą się nowe pojęcia fizyczne. Zajmujemy się tylko pracami pionierskimi dla nauki, polegającymi na odkrywaniu nowych i niespodziewanych dróg rozwoju; zajmujemy się przygodami, jakich doznaje myśl naukowa, stwarzając wiecznie zmieniający się obraz wszechświata. Pierwsze i zasadnicze kroki zawsze mają charakter rewolucyjny. Stare pojęcia, uznane przez wyobraźnię naukową za zbyt ciasne, zostają zastąpione przez nowe. Dalszy rozwój w wytkniętym raz kierunku ma już raczej charakter ewolucji, dopóki w kolejnym punkcie zwrotnym nie zajdzie potrzeba opanowania nowej dziedziny. Aby jednak rozumieć przyczyny i trudności, które zmuszają do zmiany ważnych pojęć, musimy znać nie tylko wstępne tropy, ale także wnioski, jakie można z nich wyciągnąć.
Jedną z najważniejszych cech charakterystycznych współczesnej fizyki jest fakt, że wnioski wyciągane ze wstępnych tropów mają charakter nie tylko jakościowy, ale również ilościowy. Powróćmy do kamienia puszczonego z wieży. Widzieliśmy już, że jego prędkość wzrasta w miarę spadania, chcielibyśmy jednak wiedzieć znacznie więcej. Ile mianowicie wynosi ta zmiana? A także: Jakie jest położenie oraz prędkość kamienia w dowolnej chwili po rozpoczęciu spadania? Chcemy móc przewidywać zdarzenia i stwierdzać na podstawie doświadczenia, czy obserwacje potwierdzają te przepowiednie - a przez to również założenia początkowe.
Aby wyciągnąć wnioski ilościowe, trzeba użyć języka matematyki. Większość podstawowych idei w nauce jest zasadniczo prosta i może być na ogół wyrażona w języku zrozumiałym dla każdego. Jednak śledzenie rozwoju tych idei wymaga znajomości bardzo subtelnej techniki badań. Jeżeli chcemy wyciągać wnioski, które można by porównać z doświadczeniem, to matematyka jako narzędzie rozumowania jest do tego niezbędnie potrzebna. Dopóki jednak zajmujemy się tylko podstawowymi pojęciami fizycznymi, możemy się obyć bez języka matematyki. Ponieważ tej zasady staramy się na kartach naszej książki konsekwentnie przestrzegać, będziemy musieli od czasu do czasu ograniczać się do cytowania bez dowodów niektórych wyników, koniecznych do zrozumienia ważnych tropów, które pojawią się w dalszym ciągu. Cena, jaką za zrezygnowanie z języka matematyki musimy zapłacić, to mniejsza precyzja i konieczność cytowania czasem wyników bez wskazania sposobu ich uzyskania.
Bardzo ważnym przykładem ruchu jest ruch Ziemi dokoła Słońca. Wiadomo, że w tym wypadku torem jest linia zamknięta, zwana elipsą.
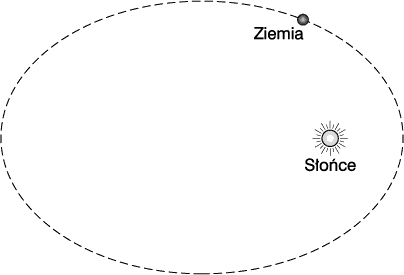
Konstrukcja wektorowego wykresu zmian prędkości wykazuje, że siła działająca na Ziemię jest skierowana do Słońca. Wszystko to razem stanowi jednak skąpą informację. Chcielibyśmy móc przewidzieć położenie Ziemi i innych planet w dowolnej chwili, chcielibyśmy przewidzieć datę i czas trwania najbliższego zaćmienia Słońca oraz wiele innych wydarzeń astronomicznych. Wszystko to jest możliwe, jednak nasz wstępny trop nie będzie sam przez się stanowił dostatecznej ku temu podstawy, albowiem teraz musimy znać nie tylko kierunek siły, lecz również jej wartość bezwzględną - jej wielkość. Zagadnienie to w natchniony sposób rozwiązał Newton. Według jego prawa powszechnego ciążenia siła, z jaką przyciągają się dwa ciała, zależy w prosty sposób od ich wzajemnej odległości. Gdy odległość wzrasta, siła maleje. Konkretnie - gdy odległość wzrasta dwa razy, siła maleje 2 × 2 = 4 razy; gdy odległość wzrasta trzy razy, siła maleje 3 × 3 = 9 razy.
Widzimy więc, że w przypadku siły ciążenia udało nam się wyrazić w prosty sposób zależność siły od odległości między poruszającymi się ciałami. Podobnie postępujemy w przypadku wszystkich innych sił, na przykład elektrycznych, magnetycznych lub innych. Próbujemy przedstawić siłę za pomocą prostego wzoru. Wzór ten będzie słuszny pod warunkiem, że wyciągnięte z niego wnioski zostaną potwierdzone przez doświadczenie.
Sama jednak znajomość siły ciążenia nie wystarcza do opisu ruchu planet. Wiemy już, że wektory przedstawiające siłę i zmianę prędkości w dowolnym, krótkim odstępie czasu mają ten sam kierunek; musimy jednak, za Newtonem, pójść o krok dalej i założyć prosty związek między długościami tych wektorów. Jeżeli wszystkie pozostałe warunki są takie same, to znaczy, jeżeli mamy to samo poruszające się ciało i zmiany prędkości rozpatrywane są w jednakowych odstępach czasu, wówczas zmiana prędkości jest, według Newtona, proporcjonalna do siły.
Tak więc do wyciągnięcia ilościowych wniosków dotyczących ruchu planet trzeba tylko dwóch uzupełniających się stwierdzeń. Jedno z nich ma charakter ogólny i ustala związek między siłą a zmianą prędkości. Drugie jest szczegółowe i ustala ścisłą zależność wchodzącej w tym wypadku w grę siły od odległości między ciałami. Pierwsze - to ogólne prawo ruchu Newtona, drugie - to jego prawo powszechnego ciążenia. Oba prawa razem wyznaczają ruch. Można to wyjaśnić, używając następującego, na pozór trochę niezręcznego rozumowania. Przypuśćmy, że potrafimy określić położenie i prędkość planety w pewnej chwili oraz że znamy siłę. Zgodnie z prawami Newtona znamy wówczas zmianę prędkości, jaka następuje w krótkim odcinku czasu. Znając prędkość początkową oraz jej zmianę, możemy znaleźć prędkość i położenie planety w końcu tego odcinka czasu. Powtarzając ten proces wielokrotnie można, nie odwołując się już do dalszych danych doświadczalnych, wykreślić cały tor ruchu. W zasadzie, w ten właśnie sposób mechanika przewiduje bieg ruchu ciała, ale użyta tu metoda nie jest zbyt wygodna. W praktyce takie postępowanie krok za krokiem byłoby niesłychanie żmudne, a także niedokładne. Na szczęście nie jest to potrzebne; matematyka dostarcza nam krótszej drogi, umożliwiając ścisły opis ruchu przy użyciu znacznie mniejszej ilości atramentu, niż potrzeba do napisania jednego zdania. Wnioski, do których się w ten sposób dochodzi, mogą być w wyniku obserwacji potwierdzone lub obalone.
Zarówno w przypadku ruchu kamienia spadającego w powietrzu, jak i w przypadku obiegu Księżyca po orbicie stwierdza się ten sam rodzaj siły zewnętrznej, a mianowicie siłę, z jaką Ziemia przyciąga ciała materialne. Newton uznał, że ruchy spadających kamieni, Księżyca i planet są tylko bardzo szczególnymi przejawami powszechnej siły ciążenia, która działa pomiędzy dwoma ciałami. W prostych przypadkach można ruch opisać i przewidzieć, posługując się matematyką. W przypadkach bardziej złożonych, gdy w grę wchodzi wzajemne oddziaływanie na siebie wielu ciał, opis matematyczny nie jest tak prosty, ale podstawowe zasady pozostają te same.
Widzimy, że wnioski, do których doszliśmy, idąc po naszych wstępnych tropach, sprawdzają się w ruchu rzuconego kamienia, w ruchu Księżyca, Ziemi i planet.
Zauważmy, że nasz system przewidywań musi być przez doświadczenie albo w całości przyjęty, albo w całości odrzucony. Żadnego z założeń nie można wyodrębnić do osobnego sprawdzenia. W przypadku planet krążących dokoła Słońca okazuje się, że system mechaniki działa znakomicie. Można sobie jednak z powodzeniem wyobrazić inny system, oparty na innych założeniach, który działałby równie dobrze.
Pojęcia fizyczne są swobodnymi tworami umysłu ludzkiego i nie są, choć by się tak mogło wydawać, w sposób jednoznaczny wyznaczone przez świat zewnętrzny. W naszym dążeniu do zrozumienia rzeczywistości jesteśmy trochę podobni do człowieka, który próbuje zrozumieć mechanizm zamkniętego zegarka. Widzi on tarczę i poruszające się wskazówki, słyszy nawet tykanie, jednakże nie zna sposobu otworzenia koperty. Może on, jeśli jest pomysłowy, stworzyć sobie pewne wyobrażenie mechanizmu - obraz, który tłumaczyłby wszystkie obserwowane fakty - nigdy jednak nie miałby całkowitej pewności, że jest to jedyny obraz, który objaśnia jego obserwacje. Nigdy też nie będzie mógł porównać swego obrazu z rzeczywistym mechanizmem; nie może sobie nawet wyobrazić możliwości ani sensu takiego porównania. Z pewnością jednak wierzy, że w miarę jak rośnie zasób jego wiedzy, stworzony przezeń obraz rzeczywistości będzie się upraszczał, objaśniając coraz to szerszy zakres jego wrażeń zmysłowych. Może on również wierzyć w istnienie wyidealizowanej granicy poznania, do której zbliża się umysł ludzki. Tę idealną granicę może nazwać prawdą obiektywną. |