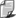Wektory

Wszystkie rozważane ruchy prostoliniowe zachodzą po linii prostej.
Zrozumienie praw przyrody uzyskujemy, rozważając przypadki najprostsze i pomijając zrazu wszelkie możliwe komplikacje. Trudno jednak zadowolić się zrozumieniem samego tylko ruchu prostoliniowego. Ruchy Księżyca, Ziemi i planet - te właśnie, do których z tak błyskotliwym sukcesem zastosowano zasady mechaniki - są ruchami po torach zakrzywionych. Przejście od ruchu prostoliniowego do ruchu po torze zakrzywionym wiąże się z nowymi trudnościami. Musimy mieć odwagę pokonania tych trudności, jeśli chcemy zrozumieć zasady mechaniki klasycznej podsunięte nam przez pierwsze tropy i stanowiące punkt wyjścia dla rozwoju nauki.
Rozważmy inne wyidealizowane doświadczenie, w którym doskonale gładka kula toczy się ruchem jednostajnym po gładkim stole. Wiemy, że jeśli kulę popchnąć, to znaczy, jeśli przyłożyć do niej siłę zewnętrzną, prędkość jej się zmieni. Przypuśćmy teraz, że pchnięcie nie następuje - jak w przypadku wózka - w kierunku ruchu, lecz w kierunku zupełnie innym, na przykład prostopadłym do kierunku ruchu. Co się stanie z kulą? Można wyróżnić trzy stadia ruchu: ruch początkowy, działanie siły i ruch końcowy, gdy siła przestała już działać. Zgodnie z prawem bezwładności obie prędkości - przed zadziałaniem siły i po jej zadziałaniu - są ściśle jednostajne. Między ruchem jednostajnym przed zadziałaniem i po zadziałaniu siły istnieje jednak różnica: zmienił się kierunek ruchu. Kierunek początkowego ruchu kuli i kierunek działania siły są nawzajem prostopadłe. Ruch końcowy nie będzie się odbywał wzdłuż żadnej z tych dwóch linii, lecz gdzieś pomiędzy nimi - bliżej kierunku siły, jeżeli uderzenie było silne, a prędkość początkowa mała, zaś bliżej początkowego kierunku ruchu, jeżeli uderzenie było delikatne, a prędkość początkowa duża. Nasz nowy wniosek, oparty na prawie bezwładności, brzmi: działanie siły zewnętrznej zmienia w ogólności nie tylko szybkość, ale i kierunek ruchu. Zrozumienie tego faktu umożliwia nam dokonanie uogólnienia, jakim jest wprowadzenie do fizyki pojęcia wektora.

Możemy w dalszym ciągu stosować naszą bezpośrednią metodę rozumowania. Punktem wyjścia jest nadal prawo bezwładności Galileusza. Wciąż jeszcze daleko nam do wyczerpania konsekwencji, jakie wynikają z tego cennego tropu, wiodącego ku rozwiązaniu zagadki ruchu.

Weźmy pod uwagę dwie kule poruszające się po gładkim stole w różnych kierunkach. Aby sobie wytworzyć konkretny obraz, możemy założyć, że oba kierunki są nawzajem prostopadłe. Na kule nie działają żadne siły zewnętrzne, toteż ich ruchy są ściśle jednostajne. Przypuśćmy dalej, że szybkości kul są równe, to znaczy, że w jednakowym odstępie czasu obie przebywają taką samą odległość. Czy będzie jednak słuszne powiedzenie, że obie kule mają taką samą prędkość? Odpowiedź może brzmieć tak lub nie! Jeśli szybkościomierze dwóch samochodów wskazują obydwa sześćdziesiąt kilometrów na godzinę, to zazwyczaj mówi się, że mają one tę samą szybkość albo prędkość - niezależnie od kierunku jazdy. Ale nauka musi na swój własny użytek tworzyć własny język, własne pojęcia. Terminy naukowe często wywodzą się z pojęć używanych w języku potocznym w związku ze sprawami życia codziennego, jednak rozwijają się zupełnie inaczej. Przekształcają się i tracą wieloznaczność, która je cechuje w języku potocznym, zyskując zarazem precyzję, umożliwiającą stosowanie ich do rozważań naukowych.

Z punktu widzenia fizyka wygodnie jest powiedzieć, że prędkości dwóch kul poruszających się w różnych kierunkach są inne. Jest to wprawdzie wyłącznie kwestią umowy, jednak wygodnie jest mówić, że cztery samochody rozjeżdżające się ze skrzyżowania w różnych kierunkach nie mają jednakowej prędkości, mimo że ich szybkościomierze wskazują wszystkie tę samą szybkość: sześćdziesiąt kilometrów na godzinę. To zróżnicowanie pojęć szybkości i prędkości pokazuje, jak fizyka, biorąc za punkt wyjścia pojęcie używane w życiu codziennym, zmienia je w sposób, który okazuje się owocny dla dalszego rozwoju nauki.

Przy pomiarze długości podaje się wynik w postaci liczby jednostek. Długość pręta może wynosić 1 metr 20 centymetrów; ciężar jakiegoś przedmiotu może być 1 kilogram 257 gramów; zmierzony odstęp czasu może wynosić tyle a tyle minut i sekund. W każdym z tych wypadków wynik pomiaru można wyrazić w postaci liczby. Istnieją jednak wielkości fizyczne, w odniesieniu do których podanie samej tylko liczby jest niewystarczające. Uznanie tego faktu oznaczało znaczny postęp w badaniach naukowych. Na przykład dla scharakteryzowania prędkości istotne są zarówno liczba, jak kierunek. Taka wielkość, posiadająca zarówno wartość liczbową, jak kierunek, nazywa się wektorem . Wygodnym symbolem takiej wielkości jest strzałka. Prędkość można przedstawić w postaci strzałki, czyli inaczej mówiąc wektora, którego długość jest w pewnej wybranej skali miarą szybkości i którego kierunek jest identyczny z kierunkiem ruchu.

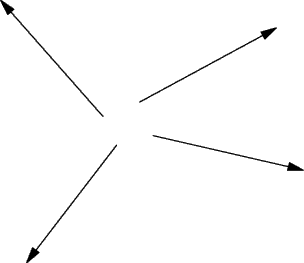
Jeżeli cztery samochody rozjeżdżają się ze skrzyżowania z równymi szybkościami, to ich prędkości można przedstawić w postaci czterech wektorów o jednakowej długości, tak jak to pokazano na rysunku. W przyjętej tu skali jeden centymetr oznacza dwadzieścia kilometrów na godzinę. W ten sposób można każdą prędkość przedstawić w formie wektora i odwrotnie, znając skalę, można z takiego wykresu wektorowego określić prędkość.

Jeżeli dwa samochody mijają się na szosie, przy czym oba szybkościomierze wskazują sześćdziesiąt kilometrów na godzinę, to prędkości ich można scharakteryzować za pomocą dwóch różnych wektorów, których strzałki wskazują przeciwne strony.

Podobnie przeciwne zwroty mają strzałki wskazujące kierunki "w górę miasta" i "w dół miasta" w nowojorskim metrze. Jednak wszystkie pociągi, jadące "w górę miasta" z taką samą szybkością, mają jednakową prędkość, którą można przedstawić w postaci jednego wektora. Wektor taki nie mówi nic o tym, które stacje pociąg właśnie mija, albo po którym z licznych, równoległych torów się porusza. Innymi słowy, według przyjętej umowy wszystkie wektory, takie jak na rysunku poniżej, można uważać za równe; leżą one albo na jednej prostej, albo na prostych równoległych, mają tę samą długość i wreszcie strzałki ich wskazują tę samą stronę.

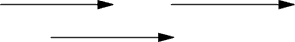
Wszystkie wektory przedstawione na następnym rysunku są inne, różnią się bowiem albo długością, albo kierunkiem, albo i jednym, i drugim.

Te same cztery wektory można narysować inaczej, tak by rozchodziły się one wszystkie z jednego punktu. Ponieważ punkt początkowy nie ma znaczenia, wektory te mogą przedstawiać prędkości czterech samochodów rozjeżdżających się z jednego skrzyżowania albo prędkości czterech samochodów, które w różnych częściach kraju poruszają się ze wskazanymi szybkościami, w określonych kierunkach.

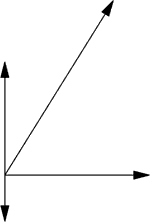
Możemy teraz zastosować obraz wektorowy do opisu omówionych uprzednio faktów dotyczących ruchu prostoliniowego. Mówiliśmy o wózku, który porusza się ruchem jednostajnym po linii prostej i zostaje popchnięty w kierunku ruchu, co zwiększa jego prędkość.

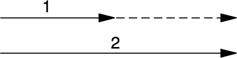
Graficznie można to przedstawić za pomocą dwóch wektorów - krótszego, oznaczającego prędkość przed popchnięciem, i dłuższego, tak samo skierowanego, oznaczającego prędkość po popchnięciu. Znaczenie wektora przerywanego jest jasne: przedstawia on zmianę prędkości, spowodowaną - jak wiemy - przez popchnięcie. W przypadku, gdy siła jest skierowana przeciwnie do ruchu, co powoduje jego zwolnienie, wykres jest nieco inny. Również i tu wektor przerywany odpowiada zmianie prędkości, jednakże jego kierunek jest w tym wypadku inny. Jest rzeczą oczywistą, że wektorami są nie tylko same prędkości, ale również ich zmiany. Jednakże każda zmiana prędkości spowodowana jest działaniem siły zewnętrznej, a zatem również siła musi być przedstawiona w postaci wektora.

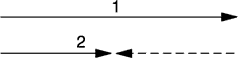
Do tego, by scharakteryzować siłę, nie wystarczy stwierdzić, jak mocno popychamy wózek; trzeba jeszcze powiedzieć, w którym kierunku go popychamy. Siła, podobnie jak prędkość lub zmiana prędkości, musi być przedstawiana w formie wektora, a nie samej tylko liczby. Zatem siła zewnętrzna jest też wektorem, a jej kierunek musi być taki sam, jak kierunek zmiany prędkości. Na obu rysunkach wektory przerywane wskazują zarówno zmianę prędkości, jak i kierunek siły.

Sceptyk może w tym miejscu zauważyć, że nie widzi korzyści z wprowadzenia wektorów. Dokonano jedynie przetłumaczenia uznanych już dawniej faktów na mało zrozumiały i skomplikowany język. Rzeczywiście, w obecnym stanie rzeczy trudno by było przekonać sceptyka, że nie ma racji. Na razie - istotnie, ma rację. Przekonamy się jednak, że właśnie ten dziwny język prowadzi do ważnego uogólnienia, w którym wektory odgrywają podstawową rolę.