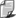Siła niech będzie z nami

Chcąc dowiedzieć się czegokolwiek o fizyce, trzeba studiować Newtona. Ale trening, jakiemu poddani są studenci podczas wykładów, zbyt często przesłania całą potęgę i rozmach stworzonej przez niego syntezy. Newton opracował ilościowy, a przy tym wyczerpujący opis zachowania ciał fizycznych. Jego legendarne skojarzenie spadającego jabłka z ruchem Księżyca podkreśla zachwycającą moc matematycznego rozumowania. Sposób, w jaki jabłko spada na Ziemię i w jaki Księżyc ją okrąża, zawarty jest w jednej wszechogarniającej koncepcji. Newton pisał: "Pragnąłbym, byśmy mogli pozostałe zjawiska przyrody wyprowadzić z zasad mechaniki za pomocą podobnego rozumowania, ponieważ mam wiele powodów, by przypuszczać, że wszystkie one mogą zależeć od pewnych sił".

Za czasów Newtona wiedziano, jak poruszają się ciała fizyczne, znano trajektorię rzuconego kamienia, regularne wychylenia wahadła, ruch ciała zsuwającego się po równi pochyłej, warunki stabilności budowli, kształt kropli wody. Newton zaś uporządkował te wszystkie zjawiska, i wiele innych, tworząc z nich jednolity system. Stwierdził, że wszelkie zmiany ruchu powodowane są przez siłę i, że reakcja ciała na działającą nań siłę zależy od własności tego ciała, zwanej masą. Każdy uczeń wie, że Newton sformułował trzy prawa ruchu. Jego pierwsze prawo to po prostu nowa wersja dokonanego przez Galileusza odkrycia, że stały, niezmienny ruch nie wymaga działania żadnej siły. Ale szczególnie interesuje nas teraz drugie prawo. Dotyczy ono siły, lecz jest nieodłączalne z jedną z tajemnic naszych rozważań - z masą. Prawo to opisuje, w jaki sposób siła wpływa na ruch.

Wielu autorów podręczników zmagało się z definicjami i logiczną spójnością drugiego prawa Newtona, które zapisujemy wtakiej oto postaci: F=ma, co oznacza, że siła równa jest iloczynowi masy i przyspieszenia. W równaniu tym Newton nie definiuje ani siły, ani masy i dlatego nie jest zupełnie jasne, czy ten wzór stanowi definicję, czy wyraża prawo przyrody. Niemniej gdy się przebrnie jakoś przez tę trudność, dociera się do najbardziej użytecznego prawa fizyki, jakie kiedykolwiek zapisano. To proste równanie ma przeogromną moc i choć wygląda niewinnie, rozwiązanie go może sprawiać wielkie kłopoty. Błee... Znowu matematyka. Proszę się nie denerwować, nie będziemy niczego rozwiązywać, tylko o tym porozmawiamy. Zresztą ten niewielki wzór stanowi klucz do zrozumienia świata mechaniki, mamy więc powody, by się przy nim na chwilę zatrzymać. (Będziemy mieli do czynienia zdwoma newtonowskimi wzorami, dla wygody więc ten nazwijmy wzorem I).

Co to jest a? To jest ta sama wielkość - przyspieszenie - którą Galileusz zdefiniował i zmierzył w Pizie oraz Padwie. Może to być przyspieszenie dowolnego obiektu: kamienia, wahadła, pocisku, a nawet statku kosmicznego Apollo. Jeśli nie nałożymy żadnych ograniczeń na zakres, którego ma dotyczyć nasze małe równanko, to a może reprezentować ruch planet, gwiazd czy elektronu. Przyspieszenie to tempo zmian prędkości. Pedał gazu w samochodzie jest tą częścią, która pozwala na zmianę wartości a. Jeśli jedziesz samochodem i w ciągu pięciu minut jego prędkość wzrosła z 15km/h do 60km/h, to znaczy że poruszasz się z pewnym przyspieszeniem. Jeśli natomiast od zera dochodzisz do 90km/h w ciągu dziesięciu sekund, to znaczy że osiągnąłeś znacznie większe przyspieszenie.

Co to jest m? Bez namysłu można powiedzieć, że m to własność materii. Jej miarą jest reakcja ciała na działąjącą na nie siłę. Im większe m, tym słabsza reakcja (a) na działającą siłę. Własność ta często bywa nazywana bezwładnością, a pełna jej nazwa to: "masa bezwładna". Galileusz odwoływał się do bezwładności przy próbach wyjaśnienia, dlaczego poruszające się ciało "wykazuje tendencję do pozostawania wruchu". Z pewnością możemy za pomocą tego równania określać wielkość masy. Przyłóżmy taką samą siłę (później dojdziemy do tego, czym jest siła) do kilku ciał i posługując się zegarem oraz taśmą mierniczą zmierzmy ruch wywołany przez tę siłę, czyli wielkość a. Ciała oróżnej masie m będą się poruszały z różnym a. Możemy przeprowadzić wiele takich eksperymentów, porównując masy wielu ciał. Gdy już się z tym uporamy, możemy sporządzić standardowy obiekt starannie wykonany z trwałego metalu i wybić na nim: 1,000 kg (to będzie nasza jednostka masy). Teraz wystarczy go umieścić w podziemiach Biur Miar i Wag w stolicach większych państw. I tak mamy już opracowany sposób przypisywania liczbowej wartości masie dowolnego ciała. Będzie to po prostu wielokrotność lub ułamek naszego kilogramowego wzorca.

No dobrze, to będzie dosyć na temat masy, ale co z F? Co to takiego F? Newton nazywał je "naporem jednego ciała na drugie" - czynnikiem powodującym zmianę ruchu. Czy w naszym rozumowaniu nie zatoczyliśmy błędnego koła? Niewykluczone, ale nie martwmy się tym na razie. Możemy teraz za pomocą naszego prawa porównywać różne siły oddziałujące na standardowe ciało. Zbliżamy się do bardzo interesującego zagadnienia. W przyrodzie istnieje wiele różnych sił. Pamiętajmy, że omawiane prawo jest prawdziwe dla dowolnego ich rodzaju. Obecnie znamy cztery rodzaje sił występujących w przyrodzie. Za czasów Newtona uczeni zaczynali poznawać jedną z nich - grawitację. Grawitacja sprawia, że ciała spadają, pociski mkną, a wahadła się wahają. Ziemia, przyciągająca wszystko, co się znajduje na jej powierzchni lub w jej pobliżu, wytwarza siłę, która jest źródłem wielkiej rozmaitości możliwych rodzajów ruchów, a nawet braku ruchu.

Możemy między innymi zastosować wzór F=ma, by wyjaśnić strukturę stacjonarnych obiektów, takich jak na przykład osoba siedząca na krześle albo, by przykład uczynić bardziej pouczającym, stojąca na wadze łazienkowej. Ziemia przyciąga Czytelniczkę z pewną siłą. Krzesło lub waga pchają ją z siłą równą co do wartości, ale przeciwnie skierowaną. Suma obu sił działąjących na osobę wynosi zero, dlatego też nie obserwujemy żadnego ruchu. Waga mówi jej, jaka siła potrzebna jest dla zrównoważenia przyciągania grawitacyjnego: 60 kG lub, wśród ludów oniskiej kulturze, które nie stosują jeszcze układu metrycznego, 132 funty. "Olaboga, od jutra się odchudzam!" Tak właśnie siła grawitacji oddziałuje na osobę. To jest właśnie to, co nazywamy ciężarem - po prostu przyciąganie grawitacyjne. Newton wiedział, że ciężar zmienia się nieco, gdy się jest w głębokiej dolinie lub na szczycie wysokiej góry, natomiast znacznie, gdy trafi się na Księżyc. Ale sama masa, czyli to, co przeciwstawia się sile, nie ulega zmianie.

Newton nie wiedział, że nacisk i popychanie, wywierane przez podłogi, krzesła, sprężyny, sznurki, wiatr i wodę, są ze swej natury siłami elektrycznymi. Pochodzenie siły nie ma znaczenia dla prawdziwości tego słynnego równania. Newton mógł analizować sprężyny, kije do krykieta, własności mechaniczne budowli, kształt kropli wody czy nawet samej Ziemi. Jeśli znamy siłę, możemy obliczyć parametry ruchu. Jeśli siła jest zerowa, zerowa jest także zmiana prędkości, co oznacza, że ciało kontynuuje swój ruch ze stałą prędkością. Jeśli podrzucisz do góry piłkę, jej prędkość zmniejsza się, aż w najwyższym punkcie toru piłka się zatrzyma i zacznie spadać coraz szybciej. Sprawia to siła grawitacji, skierowana pionowo w dół. Rzuć piłkę przed siebie. Jak opisać ten wdzięczny łuk? Rozłóżmy ruch na dwie części - na składową pionową i poziomą. Na część poziomą nie oddziałują żadne siły (śladem Galileusza musimy pominąć opór powietrza, który jest minimalny). Dlatego pozioma część ruchu odbywa się ze stałą prędkością. Wzdłuż osi pionowej obserwujemy ruch w górę i w dół, aż do zetknięcia się piłki z ziemią. Ruch złożony? Parabola! Orety!

Założywszy, że znamy masę piłki i możemy określić jej przyspieszenie, wykorzystując F=ma potrafimy dokładnie obliczyć parametry jej ruchu. Tor piłki jest zdeterminowany: jest nim parabola. Ale przecież jest wiele rodzajów parabol. Słabo uderzona piłka nie poleci daleko, mocne odbicie może posłać ją aż poza boisko. Skąd się biorą te różnice? Biorą się ze zmiennych, które Newton nazwał warunkami początkowymi. Jaka była początkowa prędkość? A początkowy kierunek? Może on przybierać rozmaite wartości, od pionowego w górę (wtym przypadku rzucający dostanie piłką w głowę) do prawie poziomego (kiedy piłka bardzo szybko spadnie na ziemię). W każdym przypadku tor ruchu, czyli trajektoria, jest zdeterminowany przez prędkość i kierunek w momencie rozpoczęcia ruchu - to znaczy przez warunki początkowe.

Chwileczkę!!!
Dochodzimy tu do głęboko filozoficznego zagadnienia. Jeśli dany jest zespół warunków początkowych dotyczących określonej liczby ciał i jeśli znane są siły oddziałujące na te ciała, to można określić, jak będzie przebiegał ich ruch... wiecznie. W świecie Newtona wszystko jest przewidywalne i zdeterminowane. Załóżmy na przykład, że wszystko w świecie składa się z atomów - cóż za dziwaczna sugestia jak na ten wykład. Przypuśćmy, że znamy początkowy stan każdego z miliardów miliardów atomów i, że wiemy, jakie siły na nie oddziałują. Załóżmy, że jakiś kosmiczny, supergigantyczny komputer mógłby przetrawić te dane i określić przyszłe położenia każdego atomu. Gdzie one wszystkie się znajdą w jakiejś chwili w przyszłości? Wynik byłby przewidywalny. Wśród tych miliardów atomów byłby mały podzbiór, który można by nazwać "Czytelnik", "Bruno" lub "Lenon". Przewidywalny, zdeterminowany... Wolny wybór byłby tylko iluzją samooszukującego się umysłu. Nauka stworzona przez Newtona była deterministyczna. Późniejsi filozofowie zredukowali rolę Stwórcy do "nakręcenia sprężyny świata" i puszczenia jej w ruch. Potem dzieje świata spokojnie już mogły się toczyć same. (Co rozsądniejsi uczeni zajmujący się tą problematyką wlatach dziewięćdziesiątych XX wieku mogliby wysunąć co do tego pewne obiekcje).

Oddźwięk, jaki teorie Newtona wywołały w filozofii ireligii, był tak samo głęboki, jak ich wpływ na fizykę. A wszystko to za przyczyną tego podstawowego równania. Strzałki mają przypominać studentowi, że siły i ich konsekwencje - przyspieszenia - skierowane są w tę samą stronę. Mnóstwo wielkości fizycznych, takich jak masa, temperatura, objętość, nie jest skierowanych wżadnym kierunku. Ale "wektory" - czyli wielkości takie jak siła, prędkość czy przyspieszenie - oznaczamy strzałkami, bo są konkretnie zorientowane w przestrzeni.

Zanim zostawimy równanie "Ef równa się ma" w spokoju, poświęćmy jeszcze chwilę jego potędze. Stanowi ono podstawę inżynierii lądowej, wodnej, akustycznej i innych jeszcze jej typów. Używa się go, aby zrozumieć napięcie powierzchniowe, przepływ cieczy w rurach, dryf kontynentów, rozchodzenie się dźwięku w stali i w powietrzu czy stabilność budowli. Teraz zaś, w miarę jak nasze komputery stają się coraz szybsze, rosną nasze możliwości rozwiązywania problemów za pomocą F=ma. Dobra robota, panie Newton!

Obiecywałem trzy prawa, a omówiłem tylko dwa. Trzecie prawo głosi, że "akcja równa jest reakcji". Ściślej mówiąc, chodzi oto, że gdy ciało A wywiera jakąś siłę na ciało B, zawsze B wywiera na A taką samą siłę, tylko przeciwnie skierowaną. Istota tego prawa leży w tym, że dotyczy ono wszystkich sił: grawitacyjnych, elektrycznych, magnetycznych i innych, niezależnie od ich rodzaju.

Co nas pcha do góry
Jak już wspomniałem, siła jest wielkością wektorową: na przykład siła grawitacji na powierzchni Ziemi skierowana jest w dół. Jaka jest natura siły, która jej przeciwdziała, która działa do góry? Czym jest siła wywierana przez krzesło na siedzącego, przez kij baseballowy na piłkę, przez gwóźdź na młotek, na czym polega nacisk helu rozciągającego balon, "ciśnienie" wody wypychającej do góry zanurzony w niej kawałek drewna? Dlaczego - co jest bardzo przygnębiające - większość z nas nie potrafi przenikać ścian? Zaskakująca, prawie szokująca odpowiedź jest taka, że wszystkie wymienione siły są różnymi przejawami oddziaływania elektrycznego.

Na początku ten pogląd wydaje się dziwaczny. W końcu, nie odczuwamy ładunków elektrycznych pchających nas do góry, gdy stajemy na wadze albo gdy siadamy na krześle. Siła ta działa pośrednio. Jak dowiedzieliśmy się od Demokryta (i zeksperymentów przeprowadzonych wXX wieku), materia wznacznej części składa się z pustej przestrzeni, a wszystko jest zbudowane z atomów. To, co spaja te atomy i pozwala wyjaśnić sztywność materii, jest oddziaływaniem elektrycznym. (Opór, jaki ciała stałe stawiają próbom przenikania przez nie, ma też coś wspólnego z teorią kwantową). Oddziaływanie to ma bardzo dużą moc: mała waga łazienkowa ma jej dość, by zrównoważyć przyciąganie całej Ziemi. Z drugiej strony, lepiej nie stawać na tafli jeziora ani wychodzić przez okno z mieszkania na dziesiątym piętrze. W wodzie, a szczególnie w powietrzu, atomy tkwią zbyt rzadko, by mogły zapewnić sztywność niezbędną dla zrównoważenia ciężaru człowieka.

W porównaniu z oddziaływaniem elektrycznym, które spaja materię i nadaje jej sztywność, grawitacja jest bardzo słaba. Jak słaba? Przedstawiam zawsze następujące doświadczenie. Biorę kawałek drewna, powiedzmy listwę odługości 30 cm, i w połowie zaznaczam biegnącą dokoła niej linię. Unoszę listwę pionowo do góry, podpisuję górną część "góra", a dolną część "dół". Trzymając ją za górną część, pytam: "Dlaczego dolna część pozostaje na miejscu, mimo, że cała Ziemia ciągnie ją do dołu?" Odpowiedź brzmi: "Bo jest mocno sczepiona z częścią górną za pośrednictwem sił elektrycznych, które spajają atomy składające się na drewno. A człwiek trzyma górną część". Racja.

By zbadać, o ile potężniejsze od grawitacji (Ziemi przyciągającej "dół") są siły elektryczne, które spajają górę z dołem, przepiłowuję listwę na pół wzdłuż zaznaczonej linii (zawsze chciałem być nauczycielem zajęć praktyczno-technicznych). W ten sposób za pomocą piły zredukowałem praktycznie do zera siły elektryczne wiążące "górę" z "dołem". Teraz, na moment przed spadnięciem na podłogę, "dół" znalazł się w konfliktowej sytuacji: mimo, że siły elektryczne zostały usunięte, góra wciąż jeszcze przyciąga grawitacyjnie "dół". Ziemia z kolei wciąż ciągnie "dół" do dołu. Dolna połowa listewki spada na podłogę. Za pomocą równania wyrażającego prawo powszechnego ciążenia możemy obliczyć różnicę między tymi dwiema siłami grawitacji. Okazuje się, że siła, z jaką Ziemia przyciąga "dół", jest ponad miliard razy większa niż ta, z którą przyciąga go "góra". Wniosek: siła elektryczna spajająca "górę" z "dołem" była przynajmniej miliard razy silniejsza niż przyciąganie grawitacyjne między tymi dwiema częściami. W sali wykładowej nie osiągniemy lepszego przybliżenia, ale okazuje się, że rzeczywiście jest ona 10⁴¹ (ta liczba to jeden zczterdziestoma i jeden zerami) razy silniejsza. Zapiszmy to w tej postaci:

100 000 000 000 000 000 000 000 000 000 000 000 000 000.

Nie sposób uzmysłowić sobie ogromu tej liczby. Nie ma mowy. Ale może ten przykład choć trochę przybliży nam 10⁴¹: Wyobraźmy sobie elektron i pozyton w odległości ćwierć milimetra od siebie. Obliczmy siłę grawitacji, z jaką się przyciągają. Teraz policzmy, jak daleko od siebie musiałyby się znaleźć te dwie cząstki, aby zrównała się z nią występująca między nimi siła przyciągania elektrycznego. Odpowiedź brzmi: około półtora tysiąca bilionów kilometrów (50 lat świetlnych). Oczywiście, wszystko to przy założeniu, że siła oddziaływania elektrycznego maleje z kwadratem odległości - tak samo jak siła grawitacji. Czy to pomogło? Grawitacja dominuje wśród wielu rodzajów ruchów, które badał Galileusz, ponieważ każda cząstka planety przyciąga ciała znajdujące się przy jej powierzchni. W badaniach nad atomami i jeszcze mniejszymi obiektami efekty grawitacji są zupełnie niedostrzegalne. W wielu innych zjawiskach grawitacja również jest bez znaczenia. Na przykład w zderzeniu dwóch kul bilardowych (fizycy uwielbiają zderzenia, są one doskonałym narzędziem pozwalającym na zdobywanie wiedzy) wpływ Ziemi zostaje zniwelowany, jeśli eksperyment odbywa się na stole. Działającą pionowo w dół siłę przyciągania ziemskiego równoważy skierowany pionowo w górę nacisk stołu. Pozostają więc tylko siły działające poziomo, gdy jedna kula uderza w drugą.

Tajemnica dwóch mas
Dzięki newtonowskiemu prawu powszechnego ciążenia można określić wartość F we wszystkich przypadkach, w których wchodzi w grę grawitacja. Wspominałem już, że Newton zapisał wzór na F w ten sposób, że siła oddziaływania jednego obiektu, powiedzmy Ziemi, na inny, powiedzmy Księżyc, zależy od ilości tworzywa grawitacyjnego zawartego w Ziemi pomnożonej przez ilość tworzywa grawitacyjnego zawartego w Księżycu. By wyrazić ilościowo tę doniosłą prawdę, Newton znalazł inny wzór, wokół którego od pewnego czasu krążymy. Wyrażony za pomocą słów przedstawia się on następująco: siła przyciągania grawitacyjnego między dwoma ciałami A i B równa jest pewnej stałej liczbowej (zazwyczaj oznaczanej literą G ) pomnożonej przez iloczyn ilości tworzywa w A i ilości tworzywa w B oraz podzielonej przez kwadrat odległości między A i B. Symbolami wyraża się to tak:

.

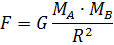Nazwijmy to Wzorem II. Nawet zagorzały wróg wszelkich rachunków musi docenić prostotę tego równania. By je nieco przybliżyć, możemy przyjąć, że A to Ziemia, B zaś - Księżyc, choć w newtonowskim sformułowaniu równanie to odnosi się do wszystkich ciał. Równanie odnoszące się do tego konkretnego układu wygląda następująco:

.

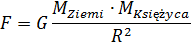Odległość między Ziemią a Księżycem sięga 400 000 km. Stała G równa się 6,67 × 10^-11 w jednostkach, które mierzą masy w kilogramach, a odległości w metrach. Ta dokładnie znana wielkość stałej określa siłę oddziaływania grawitacyjnego. Nie musimy zapamiętywać wartości tej stałej ani wogóle się nią przejmować. Zauważmy tylko, że 10^-11 świadczy otym, że jest to bardzo mała liczba. F nabiera jakiegokolwiek znaczenia tylko wtedy, gdy przynajmniej jedno z M jest ogromne, tak jak w przypadku Ziemi. Gdyby uczynić G równym zeru, życie zniknęłoby dość prędko, Ziemia poszybowałaby w przestrzeń w kierunku stycznym do jej dotychczasowego, eliptycznego toru wokół Słońca i zdecydowanie nie groziłoby nam już globalne ocieplenie.

Bardzo ciekawą rzeczą jest masa M, którą nazywamy masą grawitacyjną. Mówiłem, że jest ona miarą tworzywa w naszym przykładzie tworzywa Ziemi i Księżyca które, zgodnie ze wzorem, wytwarza oddziaływanie grawitacyjne. "Chwileczkę - słyszę jęki dochodzące z tylnych rzędów mamy teraz dwie masy. Masę m z F=ma (Wzór I) i masę M wnaszym nowym Wzorze II". No i co teraz? Słuszna uwaga, ale to nie jest żadne nieszczęście, tylko wyzwanie.

Nazwijmy te dwa rodzaje masy dużym M i małym m. Duże M jest miarą materii grawitacyjnej, która przyciąga inne ciała. Małe m to masa bezwładna, to miara materii przeciwstawiającej się sile i determinującej wielkość ruchu będącego następstwem tej siły. Są to dwa całkowicie różne atrybuty materii. Newtonowi zawdzięczamy zrozumienie tego, że z eksperymentów Galileusza i wielu innych wynika wyraźnie, iż M=m. Tworzywo grawitacyjne jest równoważne masie bezwładnej występującej w drugim prawie ruchu Newtona.

Newton nie wiedział, dlaczego te dwie wielkości są równe; po prostu przyjął ten fakt do wiadomości. Przeprowadził nawet kilka sprytnych eksperymentów, mających na celu sprawdzenie, czy rzeczywiście są równe. Z dokładnością do jednego procentu udało mu się udowodnić, że są. To znaczy M / m = 1,00. M podzielone przez m daje jeden z dwoma zerami po przecinku. Ponad dwieście lat po Isaacu Newtonie zdołano znacznie poprawić dokładność tego pomiaru. W latach 1888-1922 węgierski baron Roland Eötvös przeprowadził serię niezwykle zmyślnych eksperymentów, w których wykorzystał wahadła z aluminium, miedzi, drewna i różnych innych materiałów. Wykazał, że między tymi dwiema własnościami materii zachodzi równość z dokładnością do pięciu części na miliard. W języku matematyki wygląda to tak:

M / m = 1,000 000 000 / 0,000 000 005.
Czyli stosunek ten zawiera się między 1,000 000 005 a 0,999 999 995.

Dziś potwierdziliśmy prawdziwość tej równości do ponad dwunastu miejsc po przecinku. Galileusz udowodnił w Pizie, że dwie różne kule spadają z taką samą prędkością. Newton wykazał, dlaczego tak się dzieje. Skoro duże M równa się małemu m, siła grawitacji jest proporcjonalna do masy obiektu. Masa grawitacyjna (M) kuli armatniej może być tysiąc razy większa niż masa kulki od łożyska, a zatem siła grawitacji, której doświadczy, będzie tysiąc razy większa. Ale też jej masa bezwładna (m) będzie wykazywać tysiąckrotnie większy opór wobec tej siły niż masa bezwładna małej kulki. Jeśli te dwa ciała spuści się z wieży, to wspomniane efekty zniosą się nawzajem: kula armatnia oraz kulka od łożyska jednocześnie spadną na powierzchnię Ziemi.

Równość M i m wydawała się być niewiarygodnym zbiegiem okoliczności i dręczyła fizyków przez stulecia. Stanowiła ona klasyczny odpowiednik liczby 137. W 1915 roku Einstein włączył ten zbieg okoliczności do swej wielkiej teorii, zwanej ogólną teorią względności.

Badania barona Eötvösa nad stosunkiem M do m były najpoważniejszym, ale bynajmniej nie jedynym jego wkładem w rozwój nauki. Eötvös interesował się nauczaniem przedmiotów przyrodniczych i kształceniem nauczycieli szkół średnich. Historycy odnotowali, że jego wysiłki doprowadziły do eksplozji geniuszu. Tacy luminarze fizyki, jak: Edward Teller, Eugene Wigner, Leo Szilard, czy matematyk John von Neumann, pochodzą z Budapesztu z epoki Eötvösa. To masowe pojawianie się na początku XX wieku na Węgrzech fizyków i matematyków doprowadziło pewnych, skądinąd rozsądnych, obserwatorów do uznania, że Marsjanie założyli bazę w Budapeszcie i stamtąd zamierzają podbić naszą planetę.

Loty kosmiczne są niezwykle dramatyczną ilustracją prac Newtona i Eötvösa. Wszyscy widzieliśmy filmy kręcone na pokładach statków kosmicznych. Astronauta wypuszcza długopis, który unosi się obok niego, z wdziękiem demonstrując nam stan nieważkości. Oczywiście, ani człowiek, ani długopis nie tracą tak naprawdę ciężaru; siła przyciągania grawitacyjnego wciąż działa. Ziemia przyciąga masę grawitacyjną statku, astronauty i długopisu. Jednocześnie ruch na orbicie zdeterminowany jest przez masy bezwładne tychże obiektów zgodnie ze Wzorem II. Skoro obie masy są równe, wszystkie ciała poruszają się jednakowo. Astronauta, długopis i statek poruszają się razem w nieważkim tańcu.

Tę samą sytuację można też ująć jako swobodne spadanie, bo tym właśnie jest tak naprawdę ruch statku kosmicznego na orbicie okołoziemskiej. Księżyc w pewnym sensie też nieustannie spada na Ziemię. Nigdy do niej nie dolatuje tylko dlatego, że sferyczna powierzchnia Ziemi oddala się od niego z tą samą prędkością, z którą on spada. Tak więc, jeśli nasz astronauta spada swobodnie i jego długopis też spada swobodnie, to są w takiej samej sytuacji jak dwa ciała spuszczane z krzywej wieży. W statku kosmicznym, podobnie jak podczas spadania z wieży, waga wskazywałaby zero (gdyby tylko astronaucie udało się jakoś na niej stanąć). Stąd właśnie ten termin: "nie-ważkość". Amerykańska agencja kosmiczna NASA wykorzystuje zjawisko swobodnego spadania podczas treningów przygotowawczych dla astronautów. Aby przyzwyczaić ich do stanu nieważkości, zabiera się ich na przejażdżkę samolotem odrzutowym, który lata na dużej wysokości po torze składającym się z serii parabol (znowu ta krzywa). Podczas pikowania pasażerowie doświadczają stanu nieważkości, nie bez pewnych nieprzyjemnych doznań, które mu zazwyczaj towarzyszą. Nieoficjalnie samolot ten nazywany jest wymiotną kometą.

Tak wyglądają problemy ery kosmicznej. Ale Newton wiedział wszystko oastronaucie i jego długopisie. Już wtedy, w XVII wieku, mógłby Ci powiedzieć, co się będzie działo w statku kosmicznym.