 Zasada nieoznaczoności inaczej.
Zasada nieoznaczoności inaczej.
 Jednym
z podstawowych, a jednocześnie „tajemniczych”
wyników mechaniki kwantowej jest zasada nieoznaczoności.
Według niej niemożliwe jest jednoczesne określenie
położenia i prędkości danego obiektu z dowolną dokładnością.
Ściślej, iloczyn niepewności wyznaczenia położenia
Jednym
z podstawowych, a jednocześnie „tajemniczych”
wyników mechaniki kwantowej jest zasada nieoznaczoności.
Według niej niemożliwe jest jednoczesne określenie
położenia i prędkości danego obiektu z dowolną dokładnością.
Ściślej, iloczyn niepewności wyznaczenia położenia
 i pędu i pędu
 p
nie może być mniejszy niż połowa stałej Plancka, p
nie może być mniejszy niż połowa stałej Plancka,
 =h/2 =h/2 =1,0546·10-34
Js, czyli =1,0546·10-34
Js, czyli

Wynik ten
jest o tyle szokujący, że w mechanice klasycznej bez
dokładnej znajomości położenia i pędu nie możemy nic
powiedzieć o ewolucji układu. Dlatego często w popularnych
przedstawieniach mechaniki kwantowej zasada nieoznaczoności
ukazywana jest, jako coś niezwykłego. W niniejszym
artykule spróbujemy rozjaśnić nieco tę tajemniczość,
odwołując się do prostej analogii.
Wyobraźmy sobie, że stoimy na, peronie i chcemy zmierzyć
prędkość przejeżdżającego pociągu. Do dyspozycji mamy
zegarek i wiemy, że każdy wagon ma długość  = 20 m. Pomiaru prędkości możemy dokonać, odmierzając
zegarkiem określony odcinek czasu t i licząc
wagony, które w tym czasie nas minęły. Jeśli minęło
nas n wagonów, to pokonana przez pociąg droga
wynosi
= 20 m. Pomiaru prędkości możemy dokonać, odmierzając
zegarkiem określony odcinek czasu t i licząc
wagony, które w tym czasie nas minęły. Jeśli minęło
nas n wagonów, to pokonana przez pociąg droga
wynosi  z dokładnością do
z dokładnością do  l= l= /2.
W wyniku pomiaru otrzymamy prędkość /2.
W wyniku pomiaru otrzymamy prędkość
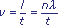
z dokładnością
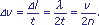
Ze wzoru
w sposób oczywisty wynika, że im większy interwał
czasu, czy też im dłuższą drogę wybieramy, tym dokładniejszy
będzie pomiar prędkości. Pamiętać jednak należy, że
zawsze będzie to prędkość średnia na odcinku
 .
Innymi słowy, położenie pociągu x w chwili
pomiaru znane jest z dokładnością .
Innymi słowy, położenie pociągu x w chwili
pomiaru znane jest z dokładnością  x=l/2=n x=l/2=n /2.
Mamy więc sytuację typową dla zasady nieoznaczoności:
możemy niezbyt precyzyjnie zmierzyć prędkość na krótkim
odcinku, ale w dość dobrze określonym miejscu, lub
uzyskać dużą dokładność pomiaru prędkości średniej,
rezygnując z precyzyjnego określenia miejsca. Ujmując
rzecz matematycznie, /2.
Mamy więc sytuację typową dla zasady nieoznaczoności:
możemy niezbyt precyzyjnie zmierzyć prędkość na krótkim
odcinku, ale w dość dobrze określonym miejscu, lub
uzyskać dużą dokładność pomiaru prędkości średniej,
rezygnując z precyzyjnego określenia miejsca. Ujmując
rzecz matematycznie,
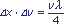
lub w języku
pędu
(1)

W mechanice
kwantowej położenie cząstki można opisać za pomocą
tzw. paczki falowej. Paczka falowa to fala, której
amplituda jest istotnie różna od zera dla skończonej
liczby okresów n, a więc w ograniczonym obszarze
 .
Oznacza to, że prawdopodobieństwo znalezienia cząstki
koncentruje się w tym właśnie obszarze. Długość .
Oznacza to, że prawdopodobieństwo znalezienia cząstki
koncentruje się w tym właśnie obszarze. Długość  fali wyznaczona, jest przez pęd p cząstki
fali wyznaczona, jest przez pęd p cząstki
(2)
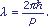
W naszej
analogii każdy wagon pociągu odpowiada jednemu okresowi
takiej fali. Możemy więc podstawić (2) do (1) i otrzymamy

Pominęliśmy
tu czynnik 2 /4,
gdyż niezbyt precyzyjna definicja /4,
gdyż niezbyt precyzyjna definicja  i
i  p
pozwala nam jedynie na dość grube oszacowanie. p
pozwala nam jedynie na dość grube oszacowanie.
Do podobnego
rezultatu możemy dojść także w inny sposób, nie posługując
się bezpośrednio formalizmem falowym. Zauważmy, że
uzyskana „zasada nieoznaczoności” (1)
jest konsekwencją „skwantowania” drogi,
którą mierzyliśmy w dyskretnych jednostkach  .
Podobną rolę odgrywa w mechanice kwantowej wielkość
fizyczna S zwana działaniem. Zazwyczaj działanie
definiujemy jako całkę względem czasu z różnicy między
energią kinetyczną i potencjalną. Dla ruchu jednostajnego
prostoliniowego działanie można wyrazić iloczynem
pędu p i drogi l, .
Podobną rolę odgrywa w mechanice kwantowej wielkość
fizyczna S zwana działaniem. Zazwyczaj działanie
definiujemy jako całkę względem czasu z różnicy między
energią kinetyczną i potencjalną. Dla ruchu jednostajnego
prostoliniowego działanie można wyrazić iloczynem
pędu p i drogi l,
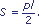
Według
mechaniki kwantowej działanie można określić z dokładnością
rzędu stałej Plancka  , ,
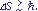
Postać
kwantowomechanicznej zasady nieoznaczoności możemy
zatem odgadnąć przez analogię, zastępując we wzorze
(1) kwant drogi  kwantem działania
kwantem działania  .
Przybierze on wówczas postać .
Przybierze on wówczas postać

Przedstawiona
analogia, choć nie jest formalnym wyprowadzeniem,
dobrze ilustruje jedną z podstawowych idei mechaniki
kwantowej: niemożność jednoczesnego określenia położenia
i pędu z dowolną dokładnością jest wynikiem istnienia
kwantu działania  . .
|