Zadanie

Zadanie.

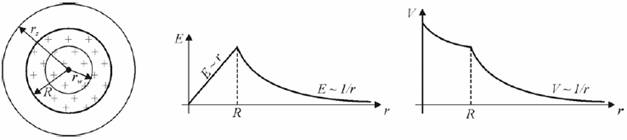
Nieprzewodzącą kulę o promieniu R naładowano jednorodnie ładunkiem o gęstości objętościowej r. Oblicz zależność potencjału i natężenia pola elektrycznego w funkcji odległości od środka kuli. Przedstaw graficznie otrzymane zależności. Przyjmij e₀ r = 1 wewnątrz kuli.

Rozwiązanie

Rozwiązanie

(a) r < R. Korzystamy z prawa Gaussa:

(1) ,

gdzie: q - ładunek zawarty wewnątrz powierzchni gaussowskiej (sfery) o promieniu r = r w < R.

stąd całkując (1) otrzymamy:

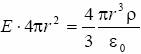
skąd:

(b) Dla r > R:

(2)

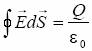
gdzie:

to ładunek zawarty w całej naładowanej kuli. dla sfery gaussowskiej o promieniu r = r z > R otrzymamy, całkując (2):

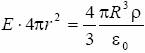
skąd:

(3) .

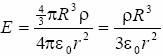Ze wzoru (3) wynika, że dla r > R natężenie pola elektrycznego naładowanej objętościowo kuli jest identyczne z polem od ładunku punktowego, znajdującego się w środku kuli.

Potencjał pola elektrycznego w naładowanej kuli liczymy korzystając ze związku:

dla r > R :

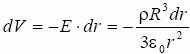
skąd:

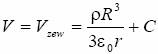
dla

czyli:

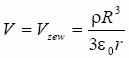
dla r < R :

skąd, po scałkowaniu:

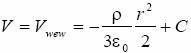
. Stałą C wyliczymy z warunku:

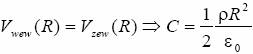
dlatego:

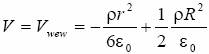
czyli:

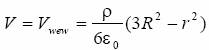
Odpowiedź

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Wzory - elektrostatyka

Elektrostatyka - Prawo Coulomba

Linki

...

Zadania z przedmiotu

Zadania z elektrostatyki