Zadanie

Zadanie.

Oblicz potencjał i wartości bezwzględne natężenia pola elektrycznego dipola o momencie p jako funkcję r i f, gdzie r oznacza odległość od środka a f kąt między osią dipola i prostą łączącą środek dipola z danym punktem.

Rozwiązanie

Rozwiązanie

Potencjał w dowolnym punkcie C, odległym od dipola o r, liczymy sumując potencjały od obu ładunków.

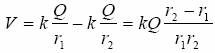
Dla

a

skąd:

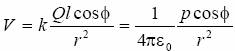
gdzie: p = q l - moment dipolowy.

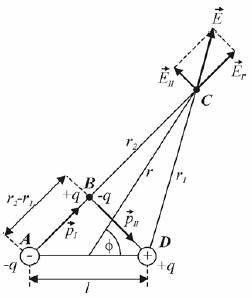
Wartość natężenia pola elektrycznego w punkcie C liczymy posługując się następującym rozumowaniem: Załóżmy, że w punkcie B umieścimy obok siebie dwa ładunki: +q i -q. Nie wpłyną one na pole pierwotne, lecz teraz już nasz układ można traktować jak dwa dipole:
p I i p II . Z trójkąta prostokątnego ABD wynika, że długość boku

a boku

Stąd wartość dipola

a dipola

Natężenie pola elektrycznego w punkcie C można traktować jako sumę wektorową pól: E_I - pochodzącego od dipola p _I (na jego osi), oraz pola E _II - pochodzącego od dipola p _II (na jego osi symetrii), czyli:

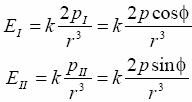
stąd:

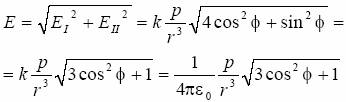
Odpowiedź

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Wzory - elektrostatyka

Elektrostatyka - Prawo Coulomba

Linki

...

Zadania z przedmiotu

Zadania z elektrostatyki