Zadanie

Zadanie.

Oblicz potencjał i natężenie pola elektrycznego na osi symetrii prostopadłej do powierzchni naładowanego ładunkiem Q krążka o promieniu R. Wykaż, że pole to staje się w skrajnym przypadku polem elektrycznym:
(a) płaszczyzny nieskończonej,
(b) ładunku punktowego.

Rozwiązanie

Rozwiązanie

Posługując się zasadą superpozycji pól znajdujemy wartości potencjału i natężenia pola elektrycznego dla punktów znajdujących się na osi z.

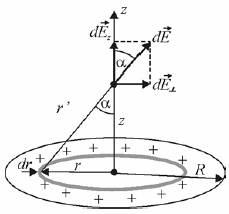
Potencjał dV od ładunku dQ, znajdującego się na pierścieniu o promieniu r i szerokości dr, w punkcie znajdującym się na osi z w odległości r' od promienia, równa się:

ale:

gdzie s - gęstość powierzchniowa ładunku, a

Stąd:

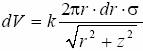
Wartość potencjału V od całego krążka równa się więc:

.

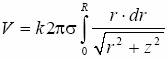
Całkując przez podstawienie otrzymujemy:

Podstawiając za s:

otrzymujemy:

(1) .

Ponieważ natężenie pola elektrycznego jest wielkością wektorową, dlatego też składową pola w kierunku osi z od ładunku znajdującego się na pierścieniu, można wyrazić wzorem:

Podstawiając za

oraz za

otrzymamy:

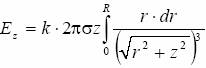
skąd:

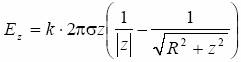
lub kładąc

(2) .

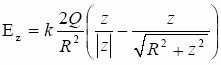Dla z >> R, czyli dla dużych odległości wyrażenie na potencjał (1) można zapisać w postaci:

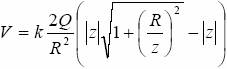
Wyłączając |z| przed nawias i stosując przybliżenie

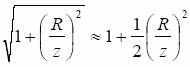
słuszne dla

otrzymamy:

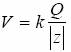
Stosując analogiczne przybliżenie do wyrażenia (2) na składową E_z pola elektrycznego otrzymamy:

Dla drugiego skrajnego przypadku, czyli dla wartości z odpowiadającym punktom leżącym w pobliżu krążka, spełniona jest relacja z << R, lub równoważna

Wartość potencjału dla tych punktów możemy otrzymać przez zastosowanie następującego przybliżenia w wyrażeniu (1)

dla R >> z. Stąd:

Natomiast dla R >> z, w wyrażeniu na składową E_z pola, możemy zaniedbać drugi człon w nawiasie, co prowadzi do wyrażenia na natężenie pola elektrycznego od naładowanej nieskończonej powierzchni:

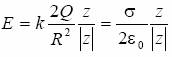
Odpowiedź

Dyskusja

 

Podstawa teoretyczna

Artykuły na stronie

Wzory - elektrostatyka

Elektrostatyka - Prawo Coulomba

Linki

...

Zadania z przedmiotu

Zadania z elektrostatyki